Introduction: Fixed-point is a great thing, but the coding can be a bit challenging. However, after finding some methods for fixed-point programming, we can still understand, master, and apply it. After all, floating-point microcontrollers are expensive, while fixed-point microcontrollers are quite affordable. The author’s first microcontroller supported floating-point, and the coding mindset has always been floating-point, just go ahead and do it. But recently, due to the need to develop some fixed-point functionalities, I was forced to learn about fixed-point implementations.
Several basic points of fixed-point computation:
-
Multiplication of fixed-point in IQ format equals addition of Q, while division reduces it.
-
Fixed-point numbers in the same IQ format can be added or subtracted directly.
-
Shifting can be used to scale numbers up or down.
The purpose of fixed-point is to scale floating-point numbers by a factor of X to compensate for the numerical errors lost during integer calculations. For example, converting 0.0001f to a fixed-point number involves multiplying the floating-point number by 2^X. If the IQ conversion number is sufficiently large, it can mitigate the errors in integer calculations. According to the IEEE 754 standard for single-precision floating-point numbers, the maximum utilization of the floating-point number encoding after the decimal point is 24 bits, therefore theoretically using IQ24 fixed-point numbers (#define _IQ24(A) (long) ((A) * 16777216.0L)) can equal the floating-point decimal error. The reason TI’s IQMATH library functions default to using IQ24 format is because of this.
Utilizing this, fixed-point calculations can achieve higher algorithm precision than single-precision floating-point, such as in high-order filter designs, where very high sampling frequencies often lead to very small coefficients in the discrete transfer function after discretization, resulting in filter errors due to floating-point quantization errors. I previously encountered a band-pass filter that could not operate well due to quantization errors, which was later resolved by splitting it into multiple filter combinations. Today, I learned that the precision of fixed-point digital calculations can even surpass that of floating-point, providing an additional method for handling such issues in the future.
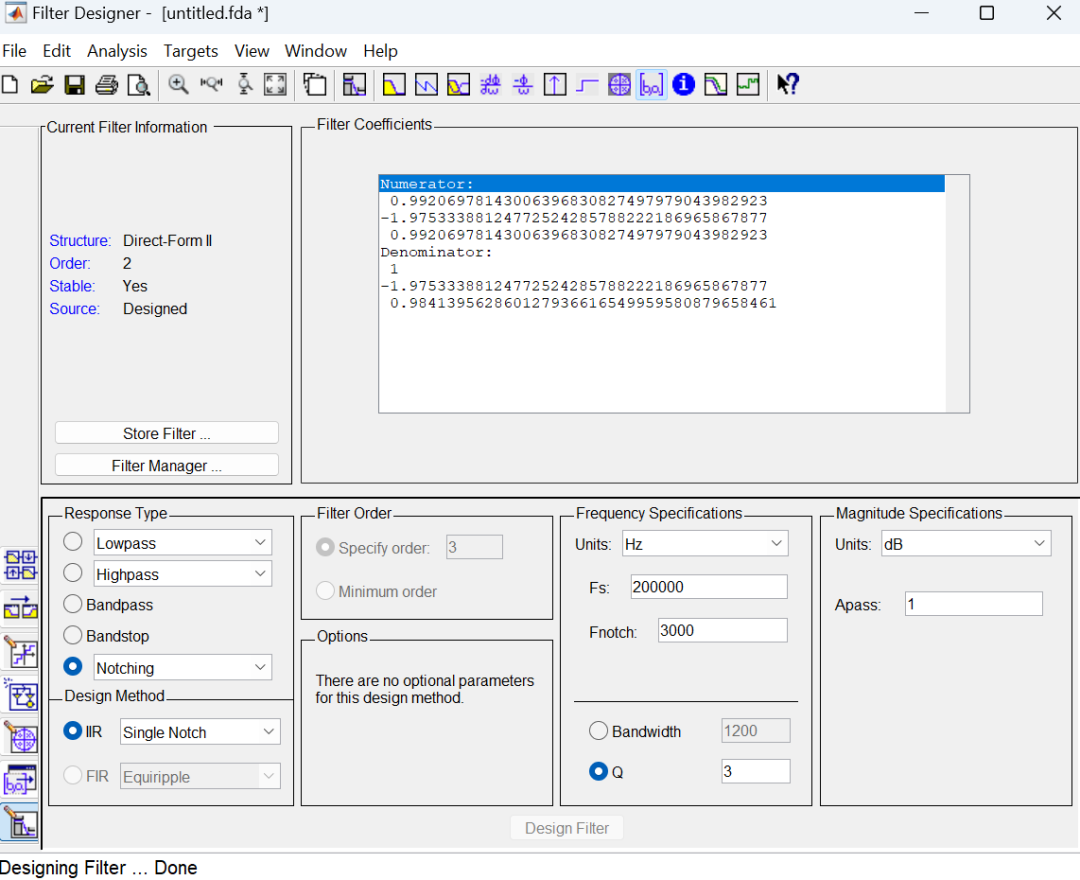
Next, let’s try a fixed-point implementation method for a PI controller to learn fixed-point programming.

Implementation:
typedef struct PIF_CTRL_LAW_DATA_IQ_TAG{
Uint16 coeff_init_flag;
_iq error_1;
_iq Integrator_output_1;
_iq Integrator_output;
_iq Integrator_gain;
_iq ts;
_iq kp;
_iq ki; /* 1/ti */
_iq pi_out;
_iq output;
_iq max_out;
_iq min_out;
Uint16 integrator_sign;
// LPF
_iq lpf_a_coeff;
_iq _1_lpf_a_coeff;
_iq lpf_out_last;
_iq lpf_out;
}PIF_CTRL_IQ_DATA_DEF;
static inline _iq piF_IQ_func( _iq error,
PIF_CTRL_IQ_DATA_DEF *p,
float32 kp,
float32 ti,
float32 lpc_fc,
float32 ts,
float32 max,
float32 min)
{
if(1u == p->coeff_init_flag) // Check if the control system is initialized
{
if(p->integrator_sign) // Anti-saturation integration, stop accumulating error when output is saturated
{
p->Integrator_output = (_IQmpy(p->ts, (error + p->error_1))) + p->Integrator_output_1;
}
else
{
p->Integrator_output = p->Integrator_output_1;
}
// Update parameters
p->Integrator_output_1 = p->Integrator_output;
p->error_1 = error;
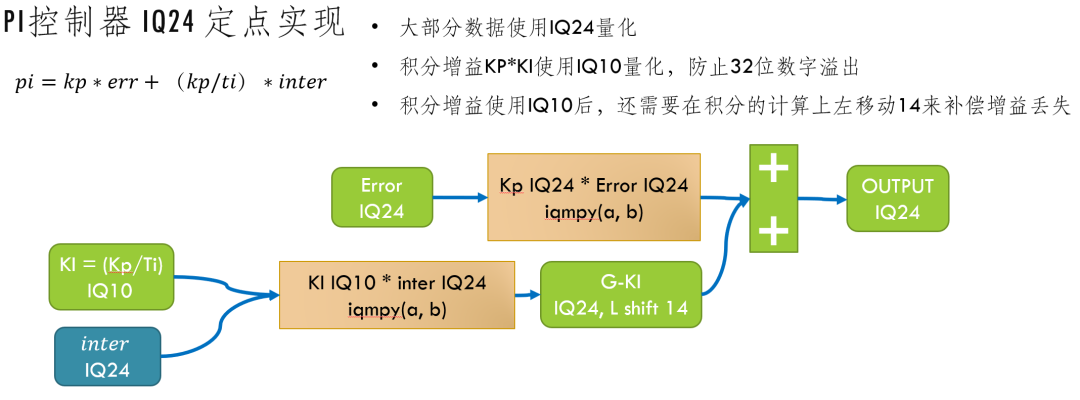
p->Integrator_gain = (_IQ10mpy(p->ki, p->Integrator_output)); // At the initial stage of integration gain, only shifted left by 10 bits, here after IQ10*IQ24, to achieve IQ24 precision, it actually needs to be shifted left by 14 bits, but after two IQ24 calculations, it needs to be shifted right by 24 bits, so shifting left 14 – right 24 means only needing to shift right by 10 to complete the calculation
p->output = _IQmpy(p->kp, error) + p->Integrator_gain;
p->pi_out = p->output;
// Limit amplitude
if(p->pi_out > p->max_out) {p->pi_out = p->max_out;}
if(p->pi_out < p->min_out) {p->pi_out = p->min_out;}
// Saturation check
p->integrator_sign = (p->pi_out == p->output)? 1u : 0u;
// LPF
p->lpf_out = _IQmpy(p->_1_lpf_a_coeff, p->lpf_out_last) + _IQmpy(p->lpf_a_coeff, p->pi_out);
p->lpf_out_last = p->lpf_out;
}
else
{
p->error_1 = 0;
p->Integrator_output = 0;
p->Integrator_output_1 = 0;
p->Integrator_gain = 0;
p->integrator_sign = 1u;
p->output = 0;
p->pi_out = 0;
p->max_out = _IQ(max);
p->min_out = _IQ(min);
// Initialize parameters
p->ts = _IQ(ts * 0.5f);
p->kp = _IQ(kp);
// Since the integration gain may be very large, to avoid overflow in 32-bit digital quantization, only IQ10 is used for conversion, which can accept loss of precision
p->ki = _IQ10(kp/ti); // L SHIFT 10BIT
p->lpf_out = 0;
p->lpf_out_last = 0;
// Low-pass filter parameter calculation
float32 lpf_rc_tao = 1.0f / (lpc_fc * 2.0f * M_PI);
/* 1ORDER LPF a = Ts/(Ts + 1/(2*pi*fc)) */
float32 lpf_a_coeff_f = ts / (ts + lpf_rc_tao);
float32 _1_lpf_a_coeff_f = 1.0f – lpf_a_coeff_f;
p->lpf_a_coeff = _IQ(lpf_a_coeff_f);
p->_1_lpf_a_coeff = _IQ(_1_lpf_a_coeff_f);
p->coeff_init_flag = 1u;
}
return(p->lpf_out);
}
My abilities are limited, and I have just started researching fixed-point programming. If there are any mistakes, please kindly point them out. Thank you.