It is well known that the max operator (or min operator) is a core component of the Bellman equation, and its efficient solution runs through various reinforcement learning algorithms, including mainstream Actor-Critic algorithms such as PPO, TRPO, DDPG, DSAC, and DACER. Friends familiar with algorithm design may have a question: why is the max operator always solved during the algorithm iteration process? Is there a possibility that a stable and convergent reinforcement learning algorithm can be designed without using the max operator? This is what we will introduce today: the Smooth Policy Iteration (SPI) architecture, the first type of adversarial reinforcement learning algorithm that breaks free from the “max operator limitation”.
Adversarial reinforcement learning is an important means to enhance scene generalization capabilities [1]. Such problems are typically modeled as zero-sum Markov games, with the core being to find the Nash equilibrium strategy—where neither the dominant strategy nor the adversarial strategy can achieve better results by unilaterally changing their strategy. The typical adversarial Bellman equation is:
where is called the dominant strategy, and is called the adversarial strategy. This is a typical nonlinear equation, which contains two operators, namely the operator or the operator, and an analytical solution is difficult to obtain directly. Policy Iteration is a common numerical solution method [2]. Based on the order of solving the and operators, existing iterative frameworks can be divided into synchronous policy iteration and asynchronous policy iteration. The former implements policy evaluation by calculating the joint value function of the dominant strategy and the adversarial strategy , and relies on this value function to perform synchronous optimization of and [3]. The latter first solves the operator to obtain the worst-case value function of the dominant strategy , and then optimizes this value function through the operator to find a better adversarial strategy. Existing research shows that synchronous policy iteration has high computational efficiency but lacks convergence guarantees and is extremely sensitive to initial values, mainly relying on manual adjustment of the learning rate ratio to obtain usable strategies. The value function sequence generated by asynchronous policy iteration has a monotonic decreasing characteristic, which can guarantee convergence to the Nash equilibrium, but the Bellman operator iteration in policy evaluation requires precise calculation of the function, leading to exceptionally low solving efficiency.
To solve this problem, Professor Li Shengbo’s research group at Tsinghua University proposed a new class of adversarial reinforcement learning solving algorithms, namely Smooth Policy Iteration (SPI). This algorithm is based on the asynchronous policy iteration framework, utilizing smooth functions to approximate the Bellman operator, and significantly reducing the solving complexity by eliminating the numerical computation of the max optimization operator [4]. First, the study found that the Bellman operator used for policy evaluation satisfies the contraction mapping property, and the policy improvement theorem that ensures the ordered update of the value function is the core guarantee of the convergence of reinforcement learning algorithms. Accordingly, three basic conditions were proposed to ensure the convergence of SPI:
(1) Contraction mapping property of the approximate operator: used to ensure the convergence of policy evaluation;
(2) Reliability of policy evaluation results: used to ensure that the error of the policy value function is bounded;
(3) Optimality of the approximate iterative framework: used to ensure that the optimal solution is the Nash equilibrium.
At the same time, the study discovered the first smooth approximation function that meets the above convergence conditions, namely the Weighted Log-Sum-Exp (WLSE) function. Fortunately, the approximation error for the max operator can be explicitly obtained for this function, and it has good properties of being continuously differentiable and satisfying the first-order Lipschitz condition, expressed as follows:
where is the approximation factor, and is the weight that satisfies normalization.
Combining the characteristics of reinforcement learning, the max function in the Bellman operator is replaced, constructing a smooth Bellman operator for approximate policy evaluation (see Figure 1). This operator uses the adversarial strategy as a weighting function, achieving value function normalization through the approximation factor. The Lipschitz property of the approximate function can derive the contraction mapping property of the smooth Bellman operator (satisfying convergence condition 1), which means that the approximate value function of the policy is a fixed point of the contraction mapping. At the same time, the bounded error of the smooth Bellman operator is derived from the error of the approximate function (satisfying convergence condition 2), and it is found that this error is inversely proportional to the approximation factor, which can control the approximation error by adjusting the approximation factor.
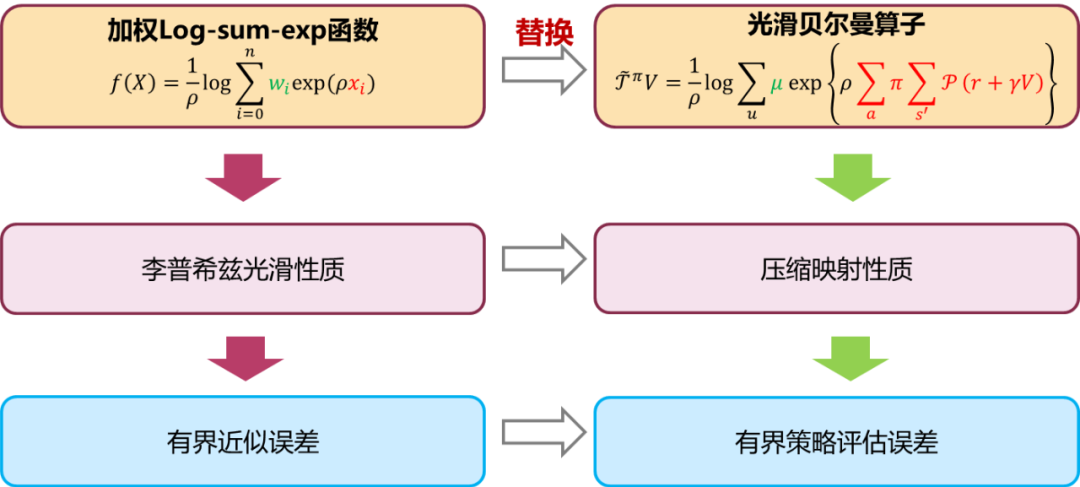Figure 1 Construction of the smooth Bellman operator using the weighted log-sum-exp function
Furthermore, the study applied the smooth Bellman operator to the iterative solving process of policy evaluation, addressing the high solving complexity problem caused by max optimization. At the same time, by referencing asynchronous policy iteration, it introduced policy improvement based on the approximate value function, constructing an efficient solving framework for the Bellman equation called Smooth Policy Iteration (SPI), as shown in Figure 2. Starting from any initial policy, policy evaluation uses the smooth Bellman operator to perform fixed-point iteration to obtain the approximate value function of the policy; subsequently, policy improvement is achieved by solving an optimization problem regarding the approximate value function to obtain a better policy. Analysis shows that when the approximation error of policy evaluation is , the value functions generated in two adjacent policy iterations satisfy:
This theory indicates that although the value function sequence of SPI does not possess strict monotonic decreasing properties, there exists an allowable error, so when the approximation factor is sufficiently large, this error approaches 0 (i.e., satisfying convergence condition 3). In summary, as long as the values taken in the iterative process continue to increase, the value function sequence exhibits a trend of monotonic decrease, coupled with the boundedness of the value function, this sequence will ultimately converge to a fixed point, which is the solution to the adversarial Bellman equation.
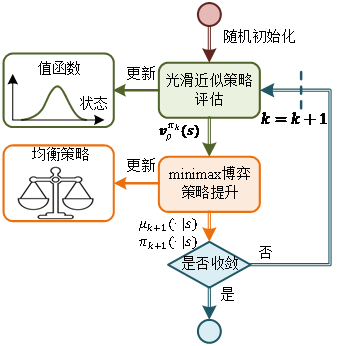Figure 2 Smooth Policy Iteration Framework
The study uses the classic two-state zero-sum Markov game problem as an example to compare the accuracy and efficiency of the SPI framework relative to the asynchronous policy iteration (API) architecture in solving the Nash equilibrium. As shown in Table 1, the SPI and API policy value functions with different approximation factors converge to a fixed value, indicating that the iterative operators possess the contraction mapping property; while compared to the true value function obtained by API, the larger the approximation factor, the smaller the approximation error of the SPI value function. Furthermore, if both iterative frameworks converge to the Nash equilibrium solution, API requires 14 iterations to reach convergence, while the SPI framework only requires 10 iterations to converge, reducing the number of iterations by 28.6%, while maintaining the optimal value function approximation error below 1%.
Table 1 Approximation Error of Smooth Policy Iteration
| Iterative Framework | Approximation Factor | Value Function | Error (%) |
|---|---|---|---|
| Smooth Policy Iteration | 1.0 | -7.62 | 8.92 |
| 5.0 | -7.23 | 3.34 | |
| 10.0 | -7.11 | 1.71 | |
| 20.0 | -7.05 | 0.86 | |
| Asynchronous Policy Iteration | — | -6.99 | 0.00 |
Furthermore, based on the SPI framework, the study introduced neural networks as the policy carrier, designing a deep reinforcement learning algorithm for solving robust policies, namely Smooth Adversarial Actor-Critic (SAAC). As shown in Figure 3, the SAAC algorithm follows the design steps of the SPI framework, updating the value network and policy network through gradient optimization. The value network constructs the target value function using the smooth Bellman operator, and its monotonic decreasing property can guide the orderly update of the value network parameters to alleviate oscillations, thereby enhancing the stability of adversarial training. The policy network synchronously updates the adversarial strategy and dominant strategy based on the output of the value network, with performance metrics as follows:
where the dominant strategy is updated using gradient descent, and the adversarial strategy is updated using gradient ascent. Considering the boundary of the adversarial strategy is crucial for the performance of the dominant strategy: a boundary that is too large can lead to a sharp increase in the adversarial strategy’s interference ability, imposing strong conservativeness on the dominant strategy. Conversely, a boundary that is too small limits the exploration space of the adversarial strategy, resulting in insufficient improvement in the generalization ability of the dominant strategy. Therefore, the study designed a data-driven model offset boundary selection method, determining the offset range based on the comparison of data from the training environment and application environment, overcoming the shortcomings of unreasonable offsets that lead to excessive conservativeness of the dominant strategy.
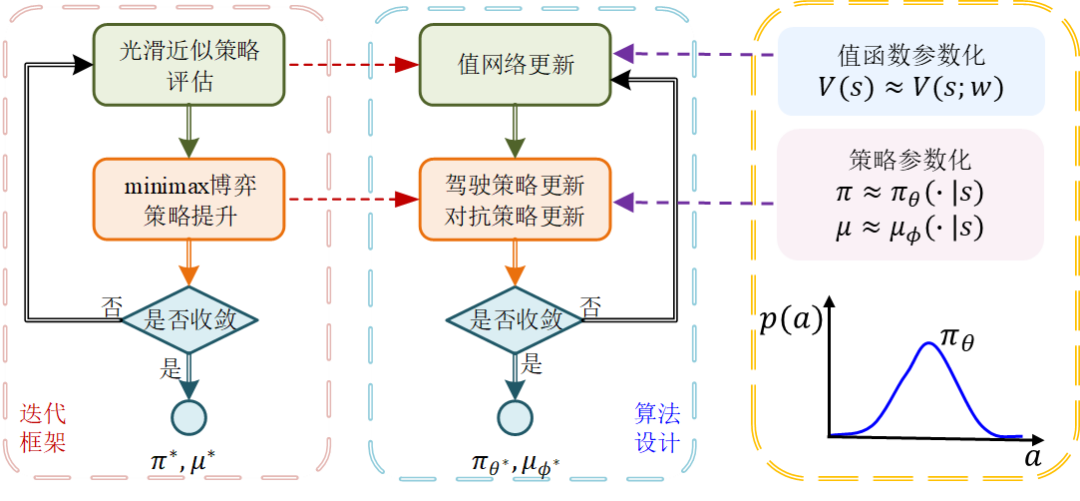
Figure 3 Correspondence between SPI Framework and SAAC Algorithm
References
- Ren Y, Duan J, Li S E, et al. Improving generalization of reinforcement learning with minimax distributional soft actor-critic[C]//23rd International Conference on Intelligent Transportation Systems. Rhodes, Greece: IEEE, 2020: 1-6.
- Li S E. Reinforcement learning for sequential decision and optimal control[M]. Singapore: Springer Verlag, 2023.
- Ren Y, Zhan G, Tang L, et al. Improve generalization of driving policy at signalized intersections with adversarial learning[J]. Transportation Research Part C: Emerging Technologies, 2023, 152: 104161.
- Ren Y, Lyu Y, Wang W, Li S E, et al. Smooth policy iteration for zero-sum Markov Games[J]. Neurocomputing, 2025, 630: 129666.