✅ Author Profile: A research enthusiast and MATLAB simulation developer, continuously improving both mindset and technology.
For code acquisition, paper reproduction, and research simulation collaboration, pleasesend a private message.
🍎 Personal Homepage: MATLAB King Assistant
🍊 Personal Motto: Walk every day, fear not the distance of ten thousand miles
🍊 Code Acquisition Method: QQ: 2307468664
🔥 Content Introduction
Batteries are an indispensable part of modern society, playing a crucial role in electronic devices, electric vehicles, and energy storage systems. Accurately estimating the Remaining Useful Life (RUL) of batteries is significant for equipment maintenance, energy management, and safe operation. Traditional RUL estimation methods mainly rely on battery capacity degradation models and cycle life data, which suffer from low accuracy and strong dependence on the initial state of the battery. In recent years, with the rise of Bayesian inference methods such as particle filtering, new ideas have emerged for achieving more accurate and robust RUL estimation.
Introduction to Particle Filter
The Particle Filter is a nonlinear, non-Gaussian state estimation method based on Monte Carlo methods. It generates a series of random samples (particles) by sampling the state space and updates the particle weights based on observation data to obtain the final state estimate. The Particle Filter has the following advantages:
-
Applicable to nonlinear, non-Gaussian systems, capable of handling complex battery models and noise.
-
Insensitive to initial state assumptions, demonstrating strong robustness.
-
Can handle non-stationary processes, suitable for dynamic changes in battery capacity degradation.
Battery SOC Estimation Based on Particle Filter
The State of Charge (SOC) of a battery represents the proportion of remaining charge to total capacity and is a key parameter for RUL estimation. Using the Particle Filter, the battery SOC can be estimated in real-time based on observation data such as battery voltage and current, thereby inferring the battery RUL.
System Model
-
State Equation: Describes the change of the internal state (SOC) of the battery, typically using electrochemical models or equivalent circuit models.
-
Observation Equation: Describes the relationship between observation data (voltage, current) and battery state (SOC).
Particle Filtering Algorithm
-
Initialization: Generate a set of particles and initialize their weights.
-
Prediction: Predict each particle based on the state equation to obtain the predicted state.
-
Update: Update each particle’s weight based on observation data and the observation equation.
-
Resampling: Resample the particles, removing those with low weights and retaining those with high weights.
-
Estimation: Estimate the battery SOC based on particle weights and infer RUL from the SOC estimate.
MATLAB Code Example
The following code example demonstrates the implementation process of battery SOC estimation based on the Particle Filter:
% Update step
likelihood = ...; % Observation likelihood function
weights = weights .* likelihood;
weights = weights / sum(weights);
% Resampling step
[~, idx] = sort(rand(N, 1));
particles = particles(idx);
weights = ones(N, 1) / N;
% SOC estimation
SOC = sum(weights .* particles);
% RUL estimation
RUL = ...; % Estimate RUL based on SOC
% Print results
disp(['Iteration: ', num2str(k), ', SOC: ', num2str(SOC), ', RUL: ', num2str(RUL)]);
endCode Explanation:
-
This code example only demonstrates the basic flow of the Particle Filter algorithm; adjustments are needed based on specific battery models and observation data in practical applications.
-
The “likelihood” part of the code needs to be calculated based on the observation equation and observation noise, and the specific implementation method should be chosen according to the actual situation.
-
The estimation of RUL needs to be calculated based on the battery capacity degradation model, and different models can be selected based on practical applications.
Conclusion
The method of estimating the remaining useful life of batteries based on the Particle Filter can effectively utilize battery state information, improving the accuracy and robustness of RUL estimation. This method is applicable to various battery types and application scenarios, with broad prospects for application.
Future Outlook
-
Combine Particle Filters with deep learning and other technologies to improve the accuracy and efficiency of RUL estimation.
-
Develop more accurate and effective battery capacity degradation models to enhance the accuracy of RUL estimation.
-
Research the integration of battery state estimation and RUL estimation.
⛳️ Operation Results
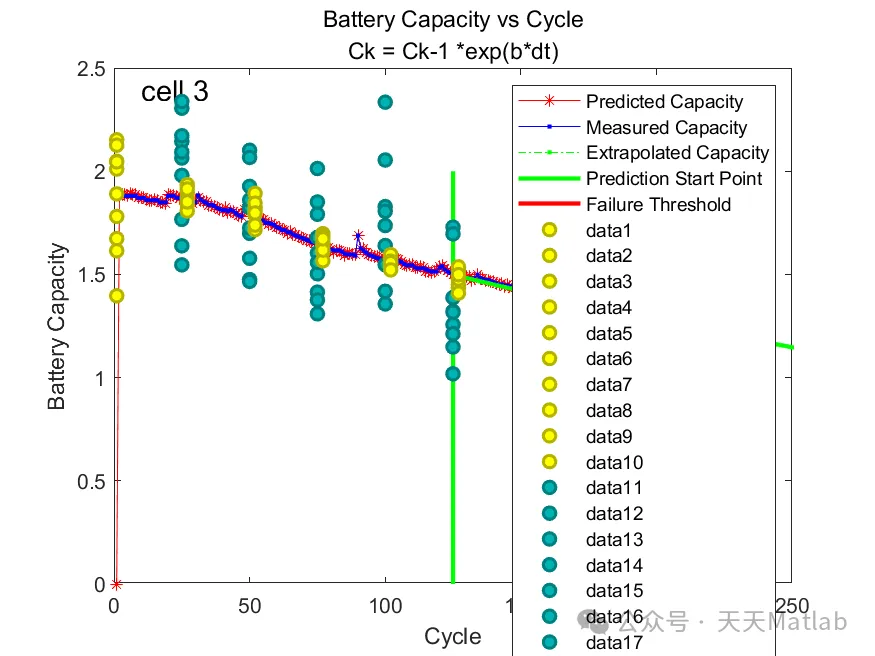
🔗 References
[1] Wu Qiang. Estimation of Lithium-Ion Battery SOC Based on Adaptive Square Root Kalman Filter Algorithm [D]. Fujian University of Technology, 2023.
[2] Shi Liping, Gong Haixia, Li Zhen, et al. Battery SOC Estimation Based on BP Neural Network [J]. Power Supply Technology, 2013, 037(009): 1539-1541. DOI:10.3969/j.issn.1002-087X.2013.09.014.
🎈 Some theoretical references are from online literature; if there is any infringement, please contact the author for deletion.
👇 Follow me to receive a wealth of MATLAB e-books and mathematical modeling materials.
🎁 Private message for complete code and data acquisition, as well as customized simulation for papers and models 🌈
🌈 Various intelligent optimization algorithm improvements and applications
Production scheduling, economic scheduling, assembly line scheduling, charging optimization, workshop scheduling, departure optimization, reservoir scheduling, three-dimensional packing, logistics site selection, cargo location optimization, bus scheduling optimization, charging pile layout optimization, workshop layout optimization, container ship loading optimization, pump combination optimization, medical resource allocation optimization, facility layout optimization, visual domain base station and drone site selection optimization, knapsack problem, wind farm layout, time slot allocation optimization, optimal distributed generation unit allocation, multi-stage pipeline maintenance, factory-center-demand point three-level site selection problem, emergency life material distribution center site selection, base station site selection, road lamp post arrangement, hub node deployment, transmission line typhoon monitoring devices, container scheduling, unit optimization, investment optimization portfolio, cloud server combination optimization, antenna linear array distribution optimization, CVRP problem, VRPPD problem, multi-center VRP problem, multi-layer network VRP problem, multi-center multi-vehicle VRP problem, dynamic VRP problem, two-layer vehicle routing planning (2E-VRP), electric vehicle routing planning (EVRP), hybrid vehicle routing planning, mixed flow shop problem, order splitting scheduling problem, bus scheduling optimization problem, flight shuttle vehicle scheduling problem, site selection path planning problem, port scheduling, port bridge scheduling, parking space allocation, airport flight scheduling, leak source localization.
🌈 Machine learning and deep learning time series, regression, classification, clustering, and dimensionality reduction
2.1 BP time series, regression prediction, and classification
2.2 ENS voice neural network time series, regression prediction, and classification
2.3 SVM/CNN-SVM/LSSVM/RVM support vector machine series time series, regression prediction, and classification
2.4 CNN|TCN|GCN convolutional neural network series time series, regression prediction, and classification
2.5 ELM/KELM/RELM/DELM extreme learning machine series time series, regression prediction, and classification
2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU gated neural network time series, regression prediction, and classification
2.7 Elman recurrent neural network time series, regression prediction, and classification
2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM long short-term memory neural network series time series, regression prediction, and classification
2.9 RBF radial basis neural network time series, regression prediction, and classification