1. Operations
In simple terms, a group ring field is a collection with operations. Let’s first look at some content related to operations. An operation is actually a mapping from one set to another:
We call an operation involving n operands an n-ary (target) operation; specifically, if n=2, it is called a binary operation. At that time, the operation is defined on a set, which means it is closed under that operation. A binary operation can be abbreviated as.
Next, let’s look at a simple example. Assume the set , with the following operation rules:
| Odd | Even | |
|---|---|---|
| Odd | Odd | Odd |
| Even | Odd | Even |
What kind of operation is this? By observation, we find that the operation’s result is always equal to the first operand; we call this operation a “projection operation”:. So how many different binary operations can be defined on this set? We can see that there are 4 “?” in the table, and each “?” has two choices: Odd or Even, leading to a total of kinds.
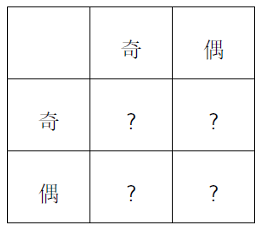
Let’s look at a slightly more challenging question: How many essentially different binary operations are there? For example, if we swap Odd and Even in Table 1, i.e., “Odd becomes Even, Even becomes Odd,” Table 1 becomes Table 2, and we say that Tables 1 and 2 represent essentially the same operation.
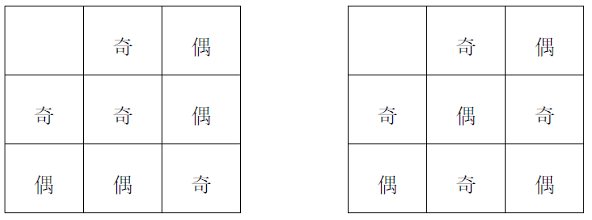
This question will not be answered due to time constraints. In groups, there are actually two very important counting tools: one is called the “Polya Counting Theorem,” and the other is called “Burnside’s Lemma.” Everyone can look into these.
If there is only one element in the set, then only one operation can be defined.
2. Groups
A non-empty set with an operation defined on it forms a group if:
-
The operation satisfies the associative law: . (At this point, the set forms a semigroup under the operation.) -
There exists an identity element such that for any element . (If both (1) and (2) hold, the set is called a monoid under the operation.) -
For any element, there exists an inverse element such that. This is denoted as.
Specifically, if the operation also satisfies the commutative law, i.e., for any element, then it is called an abelian group. Let’s look at a few simple examples:
-
The set of integers under addition forms a group, but it does not form a group under subtraction (the associative law is not satisfied); -
The complete residue system modulo n forms a group under addition, and the reduced residue system modulo n forms a group under multiplication; -
All unit roots of complex numbers form a group under complex multiplication.
Now let’s consider a somewhat special example: Does a single-element set form a group under multiplication? Is it a group? The answer is yes; we can prove it by definition. The identity element is 0, and the inverse element is also 0. Some students may wonder if this means that the multiplicative inverse of 0 is 0. Does this contradict what we learned before?
It does not contradict because here our operation rule only has this one rule; we cannot apply the operation rules from other structures here (the “0 is not invertible under multiplication” refers to the additive identity in the ring, which indeed is not invertible under multiplication in the ring. Moreover, since the group has only one element, only one operation can be defined, whether we call it “multiplication” or “addition,” it is essentially the same).
Generally, operations in groups are written in additive or multiplicative form. If written in additive form as “+”, it is denoted as. In this case, it represents the addition of n identical group elements. If written in multiplicative form as “”, it is denoted as. In general, when we talk about group structure, we only consider the operation defined in this group. Regardless of how many other operations are attached in specific instances or other algebraic structures we are familiar with (like in the previous example).
3. Subgroups
A group H is called a subgroup of G if:
-
The operation on H restricted to the set is the operation on G, i.e., for any element, .
The trivial subgroup is the subgroup consisting of the identity element. For any element, the set of all elements generated forms a cyclic subgroup of the group, denoted as.
4. Rings
A group is an algebraic structure with only one operation. A ring has two operations, called addition and multiplication. A non-empty set with operations defined on it forms a ring if:
-
The set forms a commutative group under addition. -
The multiplication operation satisfies the associative law, i.e., it is a semigroup. -
The distributive law holds: , . Usually, multiplication can be abbreviated as.
The identity element of the addition operation is denoted as 0, and the additive inverse is denoted as, called the negative element.
Since there are two operations in a ring, how many elements does a ring have at least? Clearly, it has at least two.
If the multiplication in the ring is commutative, i.e., for any element, then it is called a commutative ring. That is, the commutativity of the ring is determined by multiplication.
If there exists an element such that it is the multiplicative identity, then it is called a unital ring. Usually, the multiplicative identity is represented by 1.
For a ring, if there exists such that, then it is called a (left) zero divisor. A ring without zero divisors is called a domain (or integral domain). In a domain, the smallest positive integer that satisfies for all is called the characteristic of the ring. If no such positive integer exists, the characteristic of the ring is called 0. The characteristic of a domain is either 0 or a prime number. However, note that if the characteristic of a ring is 0, then it must be an infinite ring; if the characteristic is a prime number, the ring is not necessarily finite. When the characteristic is ,
The proof of this equation can be obtained through the combinatorial number formula, where we find that certain coefficients in the intermediate process must be divisible, leaving only a power of.
An integral domain without zero divisors is called a domain. There are many integral domains encountered in cryptography. All multiplicative invertible elements in a ring are called units. If in a domain, all non-zero elements are units, then it is a field. In other words, the multiplication in a field satisfies no zero divisors, has an identity element, is commutative, and all non-zero elements are invertible.
A field is first a ring with two operations: addition and multiplication. The set forms a commutative group under addition, with the additive identity being 0. The set forms a commutative group under multiplication, with the multiplicative identity being 1. The multiplication and addition in the set are related through the distributive law.
1. Finite Fields
A finite field is a field with a finite number of elements, also known as Galois Field. A finite field must contain at least two elements, namely 0 and 1. Under the addition and multiplication modulo p, it forms a finite field with characteristic p. Typically, a finite field containing q elements is denoted as or.
Considering the multiplicative group of a finite field of prime order p, according to the previously introduced theorem of existence of primitive roots, it is generated by a cyclic group of primitive roots modulo p. This process actually constructs a finite field of prime order. For any m, using the residue class modulo m and the addition and multiplication modulo m, we can construct a ring of order m. However, is there a finite field of any order? The answer is no; the number of elements in a finite field can only be a power of a prime number, i.e.,.
2. Field Extensions
A field extension is the process of expanding a field to a larger field while maintaining operations, called field extension. There are typically two construction methods for field extensions. The first method is to construct a residue class ring: let be a monic irreducible polynomial of degree n, i.e.,
Consider the residue class ring modulo f(x), which consists of all polynomials of degree less than n with coefficients in:
R contains polynomials. Since f(x) is irreducible, for any, there exist polynomials and of degree less than n such that
Thus, is a unit in the ring R, and the addition and multiplication (modulo f(x)) in R forms a field, thereby constructing a finite field of order.
In the above construction process, the key is to find a monic irreducible polynomial f(x) of degree n over. So, do irreducible polynomials of any degree exist over finite fields? The answer is yes; the proof method is to count the number of all n-degree polynomials and then count the number of reducible polynomials (reducible polynomials are obtained from the product of lower-degree irreducible polynomials).
Now let’s look at an example: How to construct a finite field with 4 elements? Since 4=2^2, we need to consider the binary field. is an irreducible polynomial over. The residue class ring
is the finite field with 4 elements, where. Let, then within it. Thus. It is important to note that this is not an irreducible polynomial over the finite field because. From here we can see that the reducibility of a polynomial is related to the ring/field it resides in; for example, it is irreducible over the real numbers but reducible over the complex numbers, where is the imaginary unit. However, we have another conclusion: the divisibility relation of polynomials is independent of the field they are in. This is because if two polynomials and have a divisibility relationship over a field, i.e., there exists such that , then over the extended field, since, there must also be a divisibility relationship; conversely, if two polynomials and have a divisibility relationship over the extended field, i.e., there exists such that, then due to the closure property of multiplication in the field, there must also be a divisibility relationship over the field.
Next, we will illustrate another method of field extension. Temporarily stepping outside the realm of finite fields, consider the rational field, defining addition and multiplication as: , the identity and inverse are obtained through construction. Since, by adding the imaginary unit, a field extension is obtained. Similar constructions apply to, where is a root of an irreducible polynomial. In short, by adding an element not in the field, we can extend the original addition and multiplication operations, thereby achieving a field extension.
Next, we introduce the zero polynomial:

It is important to note that in the rational field, is transcendental, meaning there is no non-zero polynomial over the rational field for which this polynomial has \\pi as a root. Now returning to the example of finite fields: for to be extended. By adding some elements while maintaining the properties of field operations. Adding the root of some irreducible polynomial, such as letting be a root of, then F, in this description, the elements in the field seem to be infinitely many, but actually due to,
it can be verified that also forms a field. If we write as x, we can see
. The two methods of field extension previously introduced are both from finite fields of prime order, but we can also extend from non-prime order finite fields, such as extending F_8 to F_{64}, just by adding a root of a quadratic irreducible polynomial over F_8 and following the previous steps for extension.
3. Operations on Extended Fields


4. Extended Fields
From the perspective of sets, from the perspective of operations, the elements in K also form a field under the addition and multiplication operations in F, so K is called a subfield of F, and F is the extension field of K. If they are both finite fields, then the order of F is a power of the order of K, so there is no subfield of order 2^3=8. The multiplicative group of a finite field is a cyclic group of order, and its generator is also called the primitive element of the field. It is important to note that in the reduced residue system modulo p^n, there is also the concept of primitive elements, but the two are very different: is a cyclic group of order, while the order of the reduced residue system modulo p^n is.
There are many important properties of extension fields, among which the more significant ones are:
These are called conjugate elements.
5. Homomorphic Mapping
Homomorphic mapping refers to a mapping that preserves operations from one algebraic structure (group, ring, field, etc.) to another. The “homomorphic” in homomorphic encryption also means this, that it preserves operations.

It is worth mentioning that the definition of homomorphic encryption strictly also considers the role of the decryption function: a semantically secure encryption scheme must be probabilistic, where the same plaintext corresponds to multiple ciphertexts, so homomorphic encryption requires that the result of decrypting the sum of the ciphertexts corresponding to a and b after encryption must be consistent with the result of decrypting the sum of a and b.
Next, we introduce simple homomorphism, full homomorphism, and isomorphism:

Now let’s look at the relationship between finite fields and isomorphism mentioned earlier: under isomorphism, there is only one finite field of order (size) q^n. For irreducible polynomials of degree n, and are both finite fields of order q^n, then they are isomorphic. This conclusion is very helpful for accelerating algorithm implementations; for example, the S-box of the SM4 algorithm and the AES algorithm are affine equivalent, both utilizing finite field inverse operations. If we can find an isomorphic mapping between the two, we can directly convert the operations of SM4’s S-box into those of AES, thereby leveraging the specialized instruction set of AES for acceleration. Another example is in elliptic curve cryptography, where self-homomorphic mappings of elliptic curves are used for acceleration. Another special example: let and be two roots of an irreducible polynomial, then under the mapping, , as previously described .

6. Polynomials over Finite Fields
All polynomials over finite fields form a ring, and this ring has excellent properties:

Finally, let’s introduce the cyclotomic polynomial, which has important applications in homomorphic encryption and lattice-based cryptography.

The above is defined through the decomposition of cyclotomic polynomials over the complex field. It can be seen that it is a monic polynomial of degree. Defined through a recurrence relation:

The following formula is very common in lattice-based cryptography and homomorphic encryption, for example, it is very helpful in the NTT fast implementation:

With the decomposition, we can use the Chinese remainder theorem of the polynomial ring over the field for some acceleration:

Guest Speaker:Liu Renzhang, Cryptography Expert, PhD in Applied Mathematics
Notes Organized by:Pei Junling, Nankai University