Have you ever wondered how a website generates a password after you enter “2333!@#¥” when setting it?
How are the widely used encryption algorithms generated? How do they protect online financial activities worldwide? How do hackers decipher passwords? In fact, all of these stem from a mathematical problem.

(Image source: veer图库)
The Birth of Network Encryption
Since humans have been able to communicate, there has been a need for a medium to convey secret messages. To prevent important information from falling into the wrong hands, our ancestors invented many interesting encryption methods. One of the earliest means of encrypting messages was invented over 2500 years ago by the Spartan army. The sender and receiver each held a cylinder of the same size, known as the Spartan cipher stick (scytale). To encode information, the sender first wrapped a narrow piece of parchment horizontally around the cipher stick, so it wound around in circles. Then, the message was written vertically along the cipher stick. When the parchment was unwrapped, the text appeared meaningless. Only by re-wrapping it around a cipher stick of the same size could the message be revealed.

Cipher stick (Image source: Wikipedia)
Since then, generations have continued to create more complex encryption methods. One of the most complex machine encoding devices was the Enigma, invented by the Germans and used by the German army during World War II.

Enigma machine (Image source: Wikipedia)
Before 1977, anyone wanting to send encrypted messages faced an inherent problem. The sender and receiver had to meet in advance to decide which cipher to use. For example, Spartan generals needed to agree on the size of the cipher stick. Even with mass-produced Enigmas, Berlin still needed to send agents to deliver codebooks to submarine captains and tank commanders, detailing the machine settings required for encryption each day. Of course, if the enemy got hold of the codebook, they were finished.
Imagine the logistical situation of using such a cipher system for internet e-commerce. Before securely sending bank account information, we must receive a secure letter from the shopping website, informing us how to encrypt the information. Given the massive flow of information on the internet, it is likely that many secure letters would be intercepted. A cipher system suitable for the fast-paced global communication era urgently needed to be developed. Just as the mathematicians at Bletchley Park cracked the Enigma during World War II, mathematicians today have invented generations of ciphers, bringing them from spy novels to the global village. These mathematical ciphers laid the foundation for what we know as the public key cryptosystem.

(Image source: veer图库)
In fact, encryption and decryption are like locking and unlocking a door. For traditional doors, the same key is used to lock and unlock. For the Enigma, the settings used for encryption could also be used for decryption. This setting—called a key—must be kept secret. The farther apart the sender and receiver are, the more difficult it becomes to logistically transport the encryption and decryption keys. Imagine a spy chief wanting to securely receive encrypted messages from different agents without wanting those agents to see each other’s messages. Therefore, different keys need to be sent to different agents separately. Now replace the agents with millions of eager shopping website users. Such a scale of operation, while not entirely impossible, is a logistical nightmare. First, users visiting the website cannot place orders immediately because they must wait for the secure key to arrive. The World Wide Web truly becomes the “World Wide Wait.”
The public key cryptosystem is like a door with two different keys:Key A is used to lock the door, and Key B is used to unlock it. You suddenly realize that for Key A, there is no need to add any security measures. Having this key does not jeopardize security. Now imagine this door as the entrance to the security department of a company’s website. The company can freely distribute Key A to any visitor, allowing them to send encrypted messages to the website, such as credit card numbers. Although anyone can use this key to encrypt data, locking the secret behind the door, no one can read the encrypted messages of others. In fact, once the data is encrypted, the user cannot read it, not even the message they sent themselves. Only the company operating the website has Key B, and only with Key B can they decrypt and read those credit card numbers.
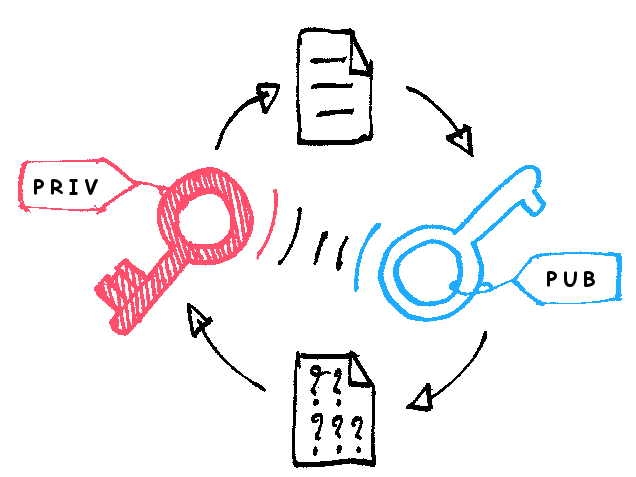
Public key encryption (Image source: Wikipedia)
The public key cryptosystem was first publicly proposed in a groundbreaking paper in 1976 by two mathematicians from Stanford University, Whitfield Diffie and Martin Hellman. They sparked a countercultural movement in the world of cryptography, challenging government agencies’ monopoly on cryptographic systems. Especially Diffie, a typical anti-establishment figure, was the kind of rebellious long-haired youth of the 1960s. Both were keen on making cryptography accessible to the public and believed it should not be a topic discussed only behind closed doors by the government, but should be used for the benefit of individuals. However, it was later revealed that some government security agencies had already been jointly promoting this cryptographic system, but it was not published in journals; instead, it was classified as top secret and shelved.

Left: Whitfield Diffie Right: Martin Edward Hellman (Image source: Wikipedia)
The Stanford University paper titled “New Directions in Cryptography” heralded the arrival of a new era in cryptographic and electronic security technology. The public key cryptosystem with two keys sounds very powerful in theory, but can this theory be applied in practice to create effective ciphers? After several years of attempts, some cryptographers began to doubt the feasibility of this encryption technology. They were concerned that this academic cryptographic system could not cope with real-world espionage activities.
RSA: The MIT Three Musketeers
The paper by Diffie and Hellman inspired many, including MIT’s Ronald L. Rivest. Unlike the rebellious Diffie and Hellman, Rivest was a traditionalist. He was taciturn, spoke gently, and acted cautiously. When he read the paper “New Directions in Cryptography,” his career goal was still to become a member of an academic institution. His dream was a professorship and theorems, not ciphers and espionage. At that time, he had no idea that the paper he was reading would lead him down another path: to create one of the most powerful and commercially successful cryptographic systems in history.

Ronald L. Rivest (Image source: Wikipedia)
After working for a while at Stanford University and Paris, Rivest joined the Computer Science Department at MIT in 1974. Like Turing, he was very interested in the interaction between abstract theory and concrete machines. He spent some time at Stanford creating intelligent robots, but his thoughts turned to a more theoretical level of computer science.
In Turing’s time, inspired by Hilbert’s second and tenth problems, the main question facing computers was whether there existed a program that could solve specific types of problems. As Turing demonstrated, no program can decide whether a mathematical fact can be proven. By the 1970s, another theoretical problem stirred the computer science community. If there indeed exists a program to solve specific mathematical problems, is it possible to analyze the speed at which that program solves the problem? If such a program were to be realized, this question was evidently very important. It required strong theoretical analytical skills but was rooted in the real world.
This combination of theory and practice was a perfect challenge for Rivest. He left the robotics project at Stanford and joined MIT to study the emerging field of computational complexity.
Rivest recalled, “One day, a graduate student came to me with this paper and said, ‘You might be interested in this.'” That was the paper by Diffie and Hellman, and he was immediately attracted. “He also said, ‘This paper discusses the definition and development of cryptography on a macro level. It would be great if you could provide some ideas too.'” The challenge in the paper encompassed all of Rivest’s interests: computation, logic, and mathematics. One problem was clearly out of consideration for the real world but was also directly related to a theoretical problem Rivest was concerned about. “In cryptography, what you care about is how to distinguish easy problems from hard problems,” he explained, “and that is precisely what computer science studies.” If a cipher is hard to crack, it must be based on a mathematically difficult problem to compute.
Rivest began attempting to construct a public key cryptosystem, selecting difficult problems from the mathematical treasury, problems that would take computers a long time to crack. He also needed someone to provide feedback on his work. At that time, MIT had begun breaking the shackles of traditional universities, strengthening interaction and communication between departments to encourage interdisciplinary research. Although Rivest worked in the Computer Science Department, he shared the same floor with colleagues from the Mathematics Department. Nearby, two mathematicians, Leonard Adleman and Adi Shamir, were in their offices.
Adleman was more sociable than Rivest but still fit the classic scholar image, with crazy and wonderful ideas about seemingly impractical things. Adleman recalled one morning when he came to Rivest’s office: “Ron was sitting there with a manuscript in hand. He said to me, ‘Have you seen this Stanford paper? It’s about encryption, ciphers, scrambling, and so on…” I replied, ‘Well, that’s nice, Ron, but I have important things to discuss, and I really don’t care about this.’ But Ron was very interested in it.” Adleman was concerned with the abstract world of Gauss and Euler. Proving Fermat’s Last Theorem was what mattered to him, not diving into the study of cryptography, a popular discipline.

Leonard Adleman (Image source: Wikipedia)
Rivest found a better listener in the nearby office—Adi Shamir, an Israeli mathematician visiting MIT. Shamir worked with Rivest to find ways to implement the ideas of Diffie and Hellman. Although Adleman was not very interested, he could not ignore the enthusiasm of Rivest and Shamir for their research: “Every time I walked into the office, they were discussing this. Most of the systems they tried failed. Since I was there, I just joined the discussion to see if their proposals were feasible.”

Adi Shamir (Image source: Wikipedia)
As they expanded their research on “difficult” mathematical problems, their cryptographic system began to take shape and incorporated more and more number theory knowledge. This was Adleman’s specialty: “Because that was my area of expertise, I could flex my muscles when analyzing their system, and most of the time, I didn’t need them.” When Rivest and Shamir proposed a system that seemed very secure, he thought he was done for. But with his number theory knowledge, it only took him one night to crack their latest cipher: “This situation repeated itself. On the way to skiing, we discussed this… even while sitting on the cable car, just before reaching the top, we were still discussing this…”
A turning point occurred one night when the three were invited to a graduate school to attend a Passover dinner. Adleman did not drink, but he remembered Rivest drinking a bottle of wine from the Passover family feast. Adleman returned home late that night. Shortly after getting home, the phone rang. It was Rivest: “I thought of another idea…” Adleman listened carefully and said, “Ron, this time you succeeded! I think your idea is correct.” They had been thinking about the problem of factorization for some time. There had not yet been any clever programming methods to find the prime factors of a number. This problem was just right. Under the influence of the Passover dinner wine, Rivest saw how to incorporate this problem into his new cipher through programming. Rivest recalled, “The first feeling at that time was fantastic. But we knew that just because it felt good at first didn’t mean the road ahead would be smooth. So we put the problem aside until the next morning.”
The next morning, when Adleman came to work at MIT, Rivest greeted him with a manuscript that had Adleman, Rivest, and Shamir’s names at the top. Adleman flipped through the manuscript, recalling what Rivest had told him on the phone the night before. “So I said to Ron, ‘Take my name off; this is your completion,’ and then we almost got into a fight over whether to keep my name. In the end, Adleman agreed to think about it. At that time, Adleman felt that authorship was not important because this paper might be the one with the lowest readership among his published works. But he also thought that for this early cryptographic system, he had worked day and night to research it, finally giving it a more mature scheme and avoiding the risk of being ridiculed for generating insecure ciphers after publication. “So I went back to Ron and said, ‘Let me be the third author.’ This is how the RSA encryption algorithm got its name.”
Rivest felt they should study how difficult the factorization problem really was: “Studying factorization at that time was a kind of profound art, and there was very little literature on it. We couldn’t say how long it would take to complete the algorithm we proposed.” However, Martin Gardner happened to know something about this problem; he was one of the world’s most popular mathematical writers. Gardner was fascinated by Rivest’s idea and asked if he would like him to write a column introducing this idea in his column in Scientific American.
After Gardner’s article was published, the response from readers made Adleman finally convinced that they had indeed done something significant:
That summer, I was in a bookstore in Berkeley. A customer was talking to someone behind the counter, and then I heard him say, “Have you seen the article about ciphers in Scientific American?” I walked over and said, “Hi, I’m one of the researchers mentioned in the article.” He turned around and said, “Can I get your autograph?” Had we ever been asked for an autograph? Never. Oh, at that time it felt… maybe our day was coming!
Gardner also mentioned in the article that as long as a stamped and addressed envelope was provided, the three mathematicians would send out preprints of their paper. “By the time I returned to MIT, we had received thousands—literally thousands—of envelopes from all over the world, including one from the Bulgarian National Security Agency…”
People began to tell the three of them that they were going to get rich. Even in the 1970s, when e-commerce was hard to imagine, people could see that their idea had enormous potential. Adleman felt that in a few months, money would be rolling in, so he went out and bought a red sports car to celebrate. It seemed that he was not the only one rewarding himself with a sports car for his mathematical achievements.
Adleman’s sports car was eventually paid off in installments from his salary at MIT. Security agencies and commercial institutions took a while to truly understand the power of the RSA encryption algorithm in password security. While Adleman drove his sports car, still thinking about Fermat’s Last Theorem, Rivest had already begun to push their ideas into reality:
We thought our scheme might have some commercial value. We went to MIT’s patent office to see if any companies were interested in bringing it to market. But it was the early 1980s, and we had almost no market. There were very few people interested at that time. The internet had not yet emerged, and personal computers were not yet widespread.
Of course, security agencies were the most interested. “Security agencies began to closely monitor the progress of this technology,” Rivest said, “but after careful study, they believed our research plan would not progress quickly.” Behind the tightly closed doors of intelligence agencies, it seemed that someone was doing the same thing. However, security agencies were also not very sure whether they could entrust the safety of agents’ lives to a few mathematicians researching ciphers. According to Ansgar Heusler from the German Federal Office for Information Security, in the 1980s, they considered using the RSA encryption algorithm in this field. They asked these mathematicians a question: Were Western mathematicians stronger in number theory than Russian mathematicians? When they received a negative answer, the idea was shelved. However, over the next decade, the RSA encryption algorithm proved its worth: it not only protected the lives of agents but also made a significant impact in the commercial field.
A Cryptographic Card Trick
Today, most transactions conducted online are protected by the RSA encryption algorithm. It is noteworthy that the mathematical calculations behind this public key cryptosystem remind one of Gauss’s clock calculator and Fermat’s theorem (Adleman’s idol), known as Fermat’s Little Theorem.

Pierre de Fermat (Image source: Wikipedia)
The addition operation on Gauss’s calculator works similarly to the familiar 12-hour dial. We know that if it is 9 o’clock now, then in 4 hours it will be 1 o’clock. This is the addition operation on the clock calculator: sum the numbers and then divide by 12. The following is the expression Gauss wrote over 200 years ago:
4+9=1 (mod 12)
The principles of multiplication and exponentiation on Gauss’s clock calculator are also the same: first calculate using a traditional calculator, then divide the result by 12, and finally take the remainder.
Gauss also realized that this calculator need not be limited to a traditional 12-hour dial. Even before Gauss explicitly proposed the concept of the clock calculator, Fermat had already discovered a fundamental law known as Fermat’s Little Theorem. Suppose there is a clock calculator with a dial time that is a prime number, represented by p. If we calculate the p-th power of a number on that calculator, the result will always return to the original number. For example, using a 5-hour dial clock calculator to calculate 2 to the power of 5. The traditional calculator’s result is 32, while on the 5-hour dial, the hour hand points to 2 o’clock. Fermat discovered that each time the calculation result was multiplied by 2, the hour hand pointed to a clock hour that changed in a regular pattern. After 5 operations, the hour hand points to the original hour and begins to repeat the previous 5 operations, as shown in the table below.
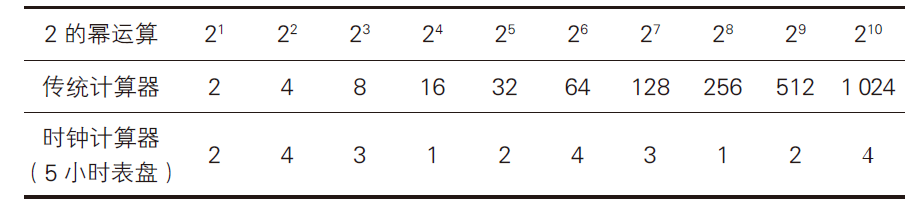
If we use a 13-hour dial clock calculator to perform the operation of 3 to the power of 13, i.e., 31, 32, …, 313, we will get:
3, 9, 1, 3, 9, 1, 3, 9, 1, 3, 9, 1, 3
At this point, the pointer does not cover all the numbers on the dial, but the hours it points to still repeat in a regular pattern. That is, if we perform the exponentiation of 3 thirteen times, the first and last operation results are both 3. No matter what prime value Fermat chooses, this magical phenomenon will occur. Using Gauss’s clock arithmetic or modular arithmetic notation, Fermat’s discovery can be described as follows: for any prime p and any hour x on the p-hour dial, we have:
xp=x (mod p)
Fermat’s discovery excited mathematicians to some extent. Primes are so magical, but what is the reason behind it? Fermat was not satisfied with experimental observation; he wanted to theoretically prove that this conclusion could hold for any prime chosen for the dial time.
In a letter written in 1640 to his friend Bernard Frénicle de Bessy, Fermat described this discovery. At least he did not treat it like Fermat’s Last Theorem, where he merely wrote a few words in the margin of a book, claiming, “I am sure I have discovered a wonderful proof, but unfortunately, the space here is too small to write it down.” Although he promised to send the proof to Frénicle, the text of that proof has been lost to this day. It was not until a century later that the relevant discussions re-entered people’s view. In 1736, Euler discovered the reason why Fermat’s prime dial pointer points back to the starting hour after performing prime exponentiation. Euler also managed to generalize Fermat’s discovery to N-hour dials, where N=p×q, with p and q being primes. Euler found that on such a dial, the hour hand begins to repeat its pointing after (p-1)×(q-1)+1 operations.
The magical prime clock arithmetic discovered by Fermat and generalized by Euler burst into Rivest’s mind late at night after the Passover dinner. Rivest thought that Fermat’s Little Theorem could be used as the key mechanism for designing a new cipher for encrypting and decrypting credit card numbers.
Encrypting credit card numbers is like starting to demonstrate a kind of card trick, but this is not an ordinary card: if you want to record how many cards are in this stack, that number can reach hundreds of digits. The user’s credit card number is one of these cards. The user places the credit card number card on top of this stack, and the website shuffles it, making the user’s card seem to “disappear.” Trying to find this card from the shuffled stack is like looking for a needle in a haystack, an impossible task for any hacker. However, the website knows the trick behind this. Thanks to Fermat’s Little Theorem, the website only needs to shuffle again to make the credit card number card reappear at the top of the stack. The second shuffle is the key that only the owner of the website—the company—can possess.

(Image source: veer图库)
The mathematical calculations used by Rivest to design this encryption trick are quite simple. The shuffling is also done through mathematical calculations. After the user places an order on the website, the computer will obtain the user’s credit card number and perform calculations. The calculations are easy to execute, but if the key is unknown, it is almost impossible to crack. This is because the calculations do not use traditional calculators but Gauss’s clock calculators.
The internet company will tell customers how many hours of the dial to use for clock calculations after they place an order. This depends on the size of the primes p and q, which are about 60 digits each. The company then multiplies the two numbers to get a third number, N=p×q. This way, the number of hours on the dial can be particularly large, reaching up to 120 digits. Each customer always uses the same clock calculator to encrypt their credit card number. The security of the password means that the company can use the same dial for several months without needing to change it.
Choosing the hour number on the dial for the website’s clock calculator is the first step in selecting the public key. Although the number N is public, the two primes p and q remain confidential. p and q are the two elements needed to crack the already encrypted credit card number.
The next step is that each customer will receive a number E, known as the encryption number. Everyone’s E is the same, and like N, it is public. To encrypt the credit card number C, the operation is performed on the website’s clock calculator to raise it to the E-th power. (Think of E as the number of times the magician shuffles the cards; after shuffling, you can hide the card you chose.) Using Gauss’s notation, it can be written as CE (mod N).
Why is this encryption algorithm so secure? After all, any hacker can see the encrypted credit card number in cyberspace, and they can also query the public key used for encryption, which contains the N-hour dial clock calculator and the E-th power operation of the credit card number. To crack this password, the hacker must find a number that, when raised to the E-th power on the N-hour dial clock calculator, will yield the encrypted credit card number. However, finding this number is quite difficult. Because the exponentiation is performed on the clock calculator rather than a traditional calculator, it is particularly difficult to crack. Using a traditional calculator, the calculation results would grow proportionally with the number of times the credit card number is multiplied, but using a clock calculator does not work that way. Thus, the hacker finds it very difficult to know the initial position of the cards because the size of the calculation result has no relation to where you start. Therefore, after E shuffles, the hacker knows almost nothing about the cards.

(Image source: veer图库)
What if a hacker launches a brute force enumeration attack on the clock calculator? That would also be impossible to succeed. The clock calculators currently used by cryptographers have N, the number of hours on the dial, which has more than 100 digits. This means that the number of hours on the dial exceeds the number of atoms in the universe. (In contrast, the encryption number E is usually much smaller.) However, if this problem cannot be solved, then how do internet companies retrieve customers’ credit card numbers?
Rivest knew that Fermat’s Little Theorem guarantees the existence of a magical decoding number D. After performing the D-th power operation on the encrypted credit card number, the original credit card number will reappear. The magician in the card trick also uses the same technique. After a certain number of shuffles, the order of the cards seems to be completely scrambled, but the magician knows that after a few more shuffles, the original order can be restored. For example, a perfect shuffle divides a stack of cards in half and then interleaves each card from both sides, so after shuffling 8 times, the original order of the cards can be restored. Of course, the magician’s art can achieve a perfect shuffle continuously 8 times. Fermat also discovered a similar clock algorithm, which allows 52 cards to return to their original order after a perfect shuffle. And Fermat’s trick is what Rivest used to crack the RSA encryption algorithm.
Although the customer’s credit card number has become difficult to find after multiple shuffles by the website, the internet company knows that, like a mathematical magician, after performing D shuffles, it will appear at the top of the stack. But only by knowing the secret primes p and q can one know D. Rivest utilized Euler’s generalization of Fermat’s Little Theorem, which uses two primes instead of one for its clock calculator. Euler had proven that on such a clock calculator, after (p-1)×(q-1)+1 shuffles, the stack of cards will return to its original order. Therefore, to know how long the repeating cycle of the clock calculator with N=p×q is, the only way is to know p and q. Thus, mastering these two primes becomes the key to cracking the RSA encryption algorithm. The number of shuffles needed to restore the “disappeared” credit card number is known only to the internet company, so p and q are also kept confidential.
Although p and q are confidential, their product N is public. Therefore, the security of Rivest’s RSA encryption algorithm is based on the extreme difficulty of factorizing N. The challenge faced by hackers is the same as that faced by Professor Cole in the early 20th century: finding the two prime factors of N.
In this issue, we are giving away this book.
Dear fans, passwords are widely used in our daily lives. How do you set your passwords? Feel free to share in the comments section.
By 12:00 noon on January 15, the top three lucky readers who leave comments and likes will receive this book from Duyuaner: “The Melodious Prime: The Two-Hundred-Year Mathematical Masterpiece of the Riemann Hypothesis.” This article is an excerpt from this book.

The Riemann Hypothesis, the unsolved mystery of prime numbers, is regarded as the “Everest” of mathematical research, attracting generations of mathematicians to delve into number theory, including many renowned figures in the history of mathematics. The discoveries made during the process of cracking this mystery have had a significant impact on fields such as e-commerce, quantum mechanics, and computer science. The author of this book narrates the story of prime numbers in a vivid and detailed manner. Reading this book allows one to appreciate the beauty of mathematics without needing a mathematical background, and to experience the journey of mathematicians up close, as well as the complex relationships of competition and cooperation among them, leading to a deeper understanding of this group of mathematicians.
(Note: All images in this article, unless otherwise specified, are illustrations from the original book)

Copyright Notice: Any form of media reproduction and excerpting without authorization is strictly prohibited, and reproduction on platforms other than WeChat is also prohibited!
Attention! WeChat has been updated! Users can set frequently read subscription accounts, which will be displayed in a large card format. To not miss the wonderful articles from Duyuan every day, please follow the steps below to “star” us:
Enter the “Science Duyuan” public account—click the three dots in the upper right corner—select “Set as Star”

This article was first published in Science Duyuan, for reprint inquiries, please contact [email protected]

Popular Articles in Duyuan Top List
Click on the article title to read directly~
1. How did Princess Elsa “turn water into ice”? This Nature article will give you the answer
2. Can sound also propagate through a vacuum? Your physics book may need to be rewritten
3. Long March 5 returns strongly! Space station, Mars exploration, lunar sample collection… they are all waiting for it
4. Are you ready? The last solar eclipse of 2019 is coming!
5. How is the research level of science in mainland China? Take a look at this list
6. Seed Hunters: That poisonous snake was only 10 centimeters away from me | Scientific American
7. This year, you may have already used these achievements from the Chinese Academy of Sciences
8. New research from Nature: The real cancer gene is not on the chromosome
9. Bears can hibernate, why can’t humans?
10.Why has Elon Musk’s space internet satellite plan met with opposition from astronomers?
Science Duyuan is the official science popularization micro-platform of the Chinese Academy of Sciences, hosted by the Science Communication Bureau of the Chinese Academy of Sciences and operated by the China Science Popularization Team, dedicated to in-depth interpretation of the latest scientific research results and scientific voices on social hot events.
For reprint authorization, cooperation, and submission inquiries, please contact [email protected]
I know you are watching me