Self-Organizing Maps (SOM): Unlocking the Topological Structure and Clustering Analysis of High-Dimensional Data

1 Algorithm Introduction

Self-Organizing Map (SOM) is an algorithm that implements unsupervised learning based on the self-organizing properties of neural networks. Its initial design inspiration comes from the way the human brain processes visual information, aiming to simulate the response of neural cells to signals and the self-organizing process in the brain.The core feature of SOM is its ability to map high-dimensional data to low-dimensional space (usually a two-dimensional plane) while preserving the original topological structure and relationships between the data. This feature gives SOM significant advantages in data dimensionality reduction, clustering, and visualization.

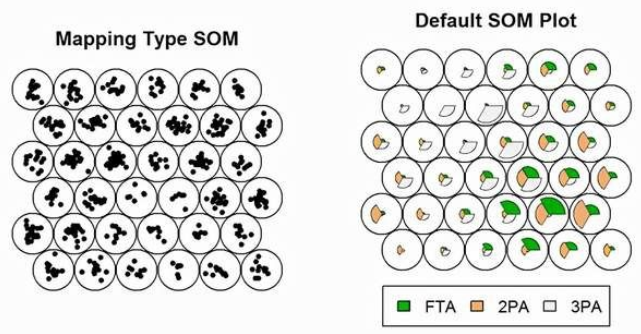
2 Algorithm Principles

The working principle of SOM is mainly based on two core concepts: competitive learning and topological preservation. In the competitive learning process, each input data finds the neuron in the network that best matches it, known as the Best Matching Unit (Best Matching Unit, BMU). Topological preservation is another important feature of SOM; in the SOM network, there is a topological relationship between neurons, forming an ordered mapping on the output layer, usually in a two-dimensional grid structure. During the training process, SOM strives to maintain the topological structure of the input data, ensuring that similar data points are close to each other in the network.

Here are the detailed steps of the SOM training process:

(1) Initialization

Before training begins, we need to randomly initialize the weight vectors of the neurons. The dimensions of these weight vectors are the same as the dimensions of the input data. For example, if we are dealing with a 10-dimensional dataset, then each neuron’s weight vector will also be a 10-dimensional vector.

(2) Input Data

Next, we will input the high-dimensional data one by one into the network. Suppose our dataset contains 1000 samples, each with 10 features, then we will sequentially input these 1000 samples into SOM for processing.

(3) Finding the Best Matching Unit (BMU)

For each input data, we need to calculate its similarity with all the neuron weight vectors. Typically, we use Euclidean distance to measure similarity. Specifically, for the input data x and the weight vector of neuron i, the Euclidean distance between them is:

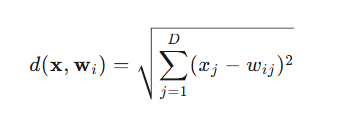
where D is the dimension of the data. By calculating the distances between all neurons and the input data, we can find the neuron that is most similar to the input data, which is the Best Matching Unit (BMU).

(4) Weight Update

After finding the BMU, we need to update the weights of the BMU and the neurons in its neighborhood to bring them closer to the input data. The weight update formula is:

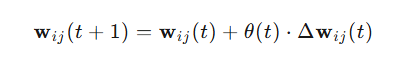
where θ(t) is the learning rate, Δw_ij(t) is the weight adjustment amount, typically the difference between the input data and the current weight:

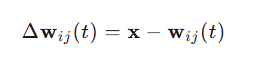The learning rate θ(t) is usually a function that decreases over time, for example: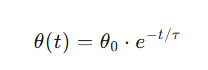

where θ₀ is the initial learning rate, and τ is the time constant.

(5) Neighborhood Adjustment

In SOM, weight updates are not limited to the BMU itself but also include the neurons in its neighborhood. The range of the neighborhood is usually a function that decreases over time. For example, we can use a Gaussian neighborhood function:

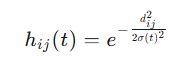
where d_ij is the distance between neuron i and neuron j, σ(t) is the neighborhood width, which is also typically a function that decreases over time:

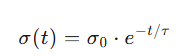
In this way, SOM gradually maps the input data to low-dimensional space during the training process while preserving the topological structure of the data.

(6) Repeat

Repeat the above steps until the network converges or reaches the preset number of training iterations. Typically, SOM requires multiple iterations of training to ensure that the network can fully learn the structure of the data.

3 Algorithm Applications

SOM has been widely applied in many fields due to its unique advantages. In the field of speech recognition, SOM can map the features of speech signals onto a two-dimensional plane, enabling the recognition and classification of different speech patterns through clustering analysis on the plane. In the field of image processing, SOM can segment images into different regions by mapping and clustering the features of image pixels, extracting feature information from each region, and providing a basis for image recognition and classification. In the field of data mining, SOM is often used for market segmentation and data clustering. For example, in market analysis, SOM can be used for customer segmentation, discovering the characteristics of different customer groups by mapping customer purchasing behavior data, thus supporting targeted marketing. In the field of bioinformatics, SOM is particularly widely used. For instance, in protein structure prediction, SOM can be used for clustering and classification of protein sequences, discovering similarities and differences between proteins by mapping protein amino acid sequences, thus providing clues for protein structure prediction.

In the field of traditional Chinese medicine, SOM can be used for analysis of traditional Chinese medicine prescriptions, syndrome diagnosis, and research on drug compatibility. For example, a research team from Beijing University of Chinese Medicine utilized the Analytic Hierarchy Process (AHP) – Self-Organizing Map (SOM) clustering – Ideal Solution Approximation Ranking Algorithm (TOPSIS) and the Traditional Chinese Medicine Inheritance Assistance Platform (V2.5) to conduct data mining research on the formulation of traditional Chinese medicine for treating perimenopausal depression, and combined with traditional Chinese medicine theory, to explore new formulations for treating perimenopausal depression (see the research process in Figure 1).SOM can also assist in distinguishing traditional Chinese medicine symptoms and perform syndrome clustering, converting clinical four diagnostic data (observation, listening, inquiry, and pulse-taking) into high-dimensional feature vectors, and through SOM dimensionality reduction, performing unsupervised clustering of patients’ symptom data, helping traditional Chinese medicine practitioners identify the group characteristics of different syndromes (such as Qi deficiency, blood stasis, etc.), and so on.

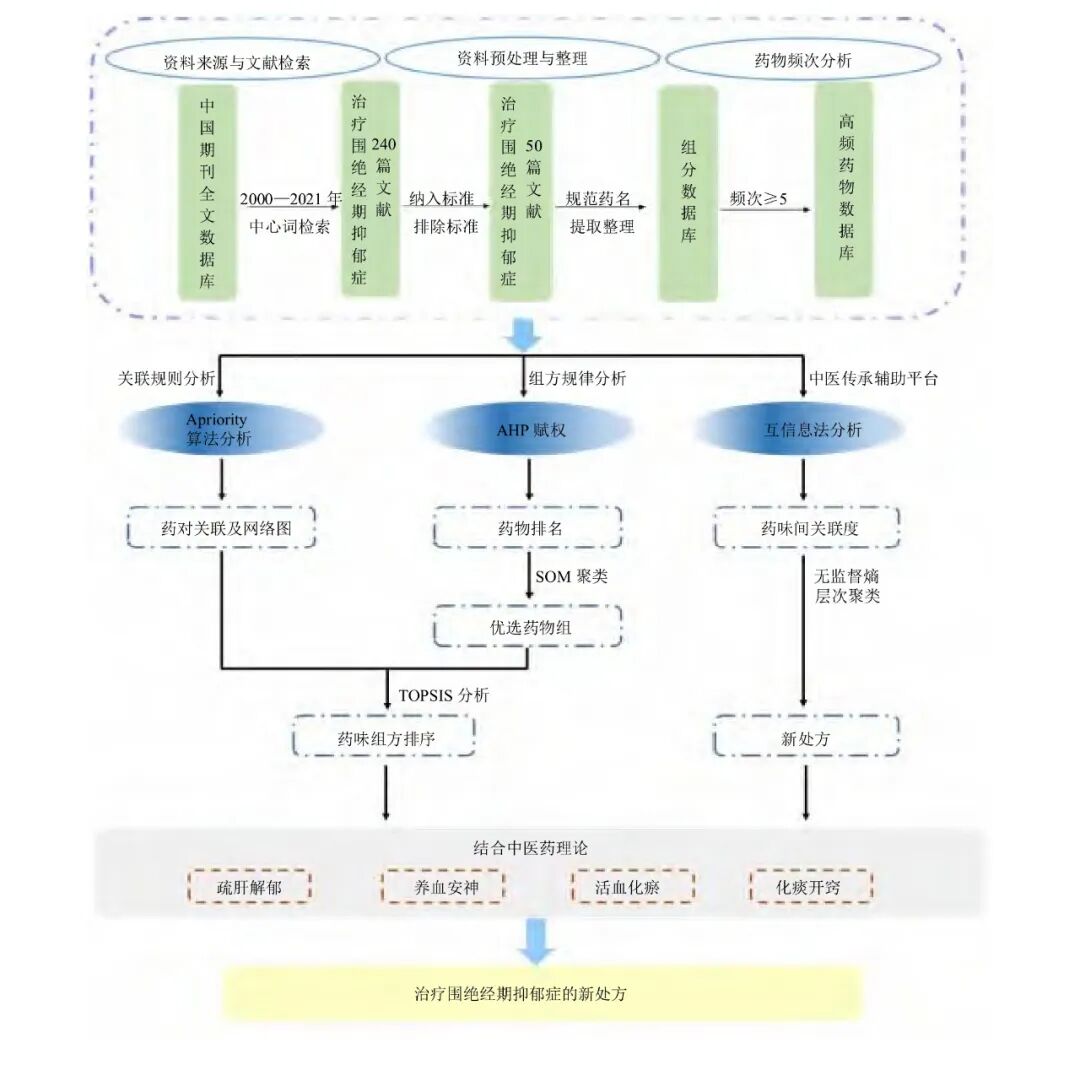Figure1 Design Process of New Formulations for Treating Perimenopausal Depression4 Conclusion

Self-Organizing Maps (SOM) as an important unsupervised learning algorithm, occupies a significant position in the fields of data science and artificial intelligence due to its unique working principles and wide range of applications. However, SOM also has some limitations. For example, the training process of SOM requires multiple iterations, resulting in high computational complexity. Additionally, SOM is sensitive to the selection of parameters such as learning rate and neighborhood range, requiring careful adjustment. To address this, improvements such as adaptive learning rates and dynamic neighborhood adjustments can significantly enhance the performance of SOM. In future research, SOM can play a greater role in more fields.

References:

[1]Self-Organizing Map (SOM) – CSDN Blog. Accessed on April 23, 2025.

https://blog.csdn.net/xhtchina/article/details/129912847.

[2] AI Learning Guide: Machine Learning – Introduction to Self-Organizing Maps (SOM) – CSDN Blog. Accessed on April 23, 2025.

https://blog.csdn.net/zhaopeng_yu/article/details/139869713.

Related posts

Leave a Comment Cancel reply