Projection Pursuit Model Based on Sparrow Algorithm

Abstract: Projection pursuit (PP) is an emerging statistical method for processing and analyzing high-dimensional data. Its basic idea is to project high-dimensional data into a low-dimensional subspace and find projections that can reflect the structure or features of the original high-dimensional data in that subspace, thereby achieving the goal of studying and analyzing high-dimensional data. It has significant advantages in overcoming the “curse of dimensionality” and addressing issues such as small samples and ultra-high dimensions. In practical applications, the selection of the optimal projection direction a for the projection pursuit model has a critical impact on the evaluation accuracy and results of the model. This paper utilizes the Sparrow Algorithm to optimize the parameters for the optimal projection direction a.

1. Sparrow Algorithm

For the basic principles of the Sparrow Algorithm, please refer to my blog: https://blog.csdn.net/u011835903/article/details/108830958

2. Projection Pursuit Model

The basic principle of the projection pursuit model is to project high-dimensional data into a low-dimensional subspace through some combination, reflecting the original high-dimensional data structure or features by minimizing the projection index, and analyzing the data structure in the low-dimensional space to achieve the goal of studying and analyzing high-dimensional data. The brief algorithm process is as follows:

Step 1: Data preprocessing. Normalize the evaluation dataset.

Step 2: Construct the projection index function. The projection pursuit method combines m-dimensional data into a one-dimensional projection value for the projection direction: In this formula, y is the ith evaluation index value of the jth group; w is the unit vector.

Step 3: Optimize the projection index function. When the projection index function reaches its maximum value, the corresponding direction is the optimal projection direction that best reflects the data features. Therefore, the problem of searching for the optimal projection direction is transformed into a nonlinear optimization problem, with the objective function and constraints as follows: where:

In this formula: σ and ρ are the standard deviation and local density of the projection values; μ is the mean of the sequence; r is the window radius for local density; d is the distance between samples; H is the unit step function, where H(x) equals 1 when x is greater than 0, and equals 0 when x is less than or equal to 0; N is the total number of evaluation samples.

3. Sparrow Algorithm Combined with Projection Pursuit

From section 2, we know that the parameter a is the object we want to optimize, so we set the dimension of the sparrow to be the number of sample groups. The fitness function is the objective function of projection pursuit.

4. Test Results

A set of case data between [0, 1] is set as follows:

% Import data, each column is an index, each row is sample data, calculate the projection evaluation value for each sample
data =[0.71   0.00   0.37   0.01   0.15   0.00   0.37 
0.14   0.59   0.00   1.08   1.00   0.59   0.97 
0.57   0.43   0.11   0.98   0.01   0.73   0.83 
1.00   0.40   0.69   0.80   0.28   1.00   0.40 
0.73   0.66   1.00   0.00   0.88   0.90   0.53 
0.00   0.74   0.29   0.12   0.75   0.06   0.00 
0.84   0.86   0.86   0.61   0.97   0.64   0.50 
0.11   1.00   0.37   0.08   0.49   0.50   0.73 
0.27   0.09   0.49   0.39   0.94   0.86   0.40 
0.70   0.36   0.49   0.58   0.18   0.45   1.00 ];

The sparrow parameters are set as follows:

SearchAgents_no=30; % Population size
Max_iteration = 2000; % Maximum number of iterations
dim = size(data,2);
lb = 0.01; % Lower bound
ub = 1; % Upper bound
fobj = @(a) fun(data,a);
[Best_score,Best_pos,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); % Start optimization

The projection pursuit results are as follows:

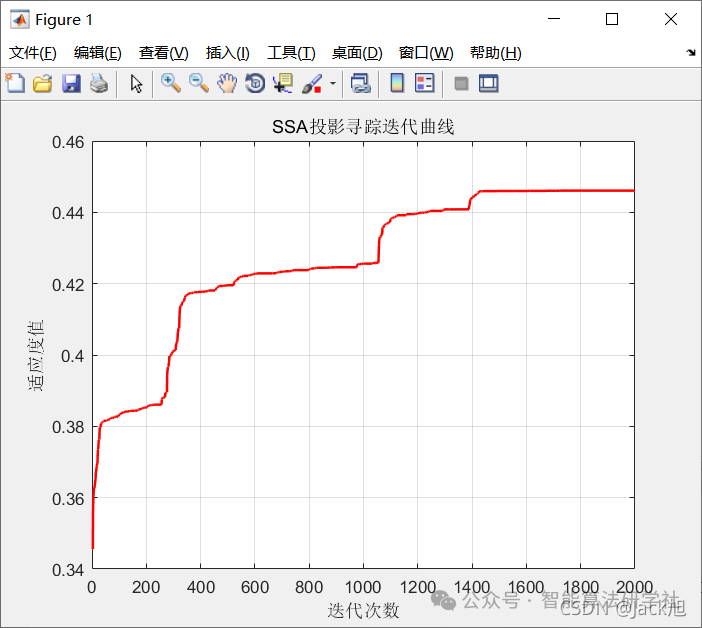
The optimal projection vector a is: 0.2358 0.3284 0.3934 0.4779 0.0556 0.5114 0.4345

The projection values are:

0.486867427615660 1.52175142407054 1.52174671413937 1.72168202129490 1.52174833709580 0.486864069973941 1.70884617442894 1.13825810216718 1.13825881537161 1.42787940606387

5. References

[1] Cui Dongwen. Flock Optimization Algorithm – Projection Pursuit Drought and Flood Disaster Assessment Model [J]. Advances in Water Resources and Hydropower Science and Technology, 2016, 36(02): 16-23+41.

6. Matlab Code

Click “Read the original text” to get it!