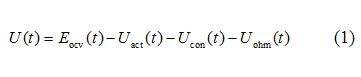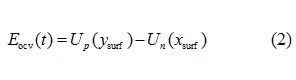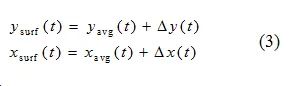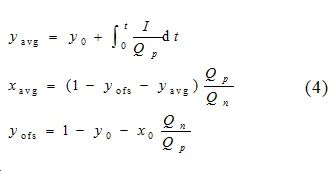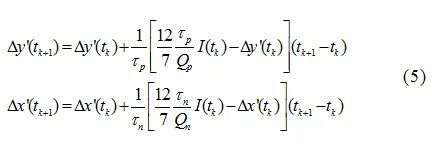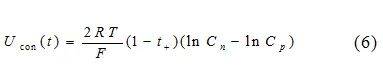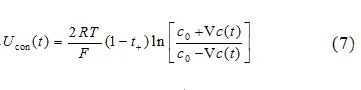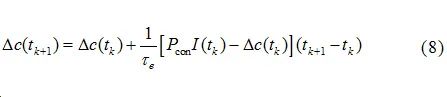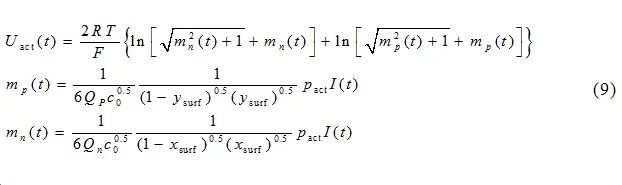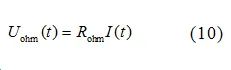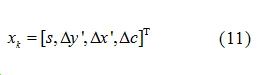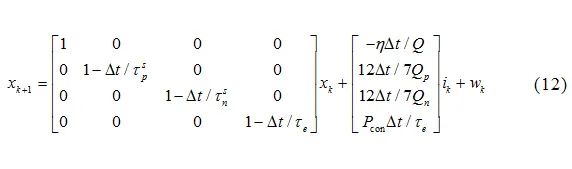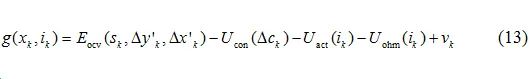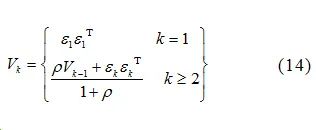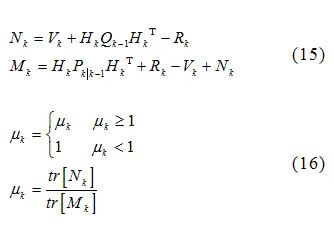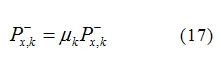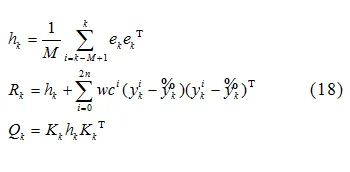Source: Power Technology Magazine
An accurate battery model is crucial for electric vehicle battery management systems, as it ensures accurate estimation of the battery’s state of charge (SOC).
The electrochemical model is a mechanistic model that describes the internal electrochemical reaction conditions of the battery, and extensive research has been conducted both domestically and internationally on electrochemical models. The pseudo-two-dimensional model (P2D), based on porous electrode theory and concentration theory, is a classic electrochemical model that provides a detailed description of the internal reactions of the battery, resulting in high computational accuracy. However, the simulation process of the P2D model is time-consuming, making it inefficient for practical engineering applications[1]. The single particle model simplifies the electrochemical model by representing the entire electrode with a spherical particle, which has a simple structure and fast computation. However, it ignores the liquid phase diffusion process, leading to significant errors under high rate currents. Literature[2] improves the single particle model by using a parabolic approximation method to simplify the description of liquid phase diffusion, enhancing the model’s accuracy under high current conditions, but the simulations were only validated numerically without experimental analysis. Literature[3] builds upon this model, conducting dynamic condition experiments for parameter identification and validating accuracy through experiments. However, the designed experiments are relatively complex, and the parameters are identified one by one, which can lead to cumulative errors due to the influence of previously identified parameters.
Genetic algorithms are a method for global optimization of variables. Literature[4] utilizes genetic algorithms for parameter identification of electrochemical models, achieving good results, but the study did not consider the changes in parameters during the discharge process. Common methods for estimating battery SOC include open-circuit voltage method, ampere-hour integration method, and Kalman filtering method, among which the Kalman filtering method is a model-based unbiased estimator of SOC that effectively reduces errors and maintains accuracy even under significant current changes. This paper employs the extended single particle (ESP) model, utilizing genetic algorithms for parameter identification, considering the variation of parameters at different SOC levels, and performing multiple phased identifications. Charging and discharging experiments validate the accuracy of the model and parameter identification results. Based on the ESP model and Kalman filtering algorithm, an improved adaptive strong tracking Sigma point Kalman filtering algorithm is established to estimate SOC.

Lithium-Ion Battery ESP Model Establishment
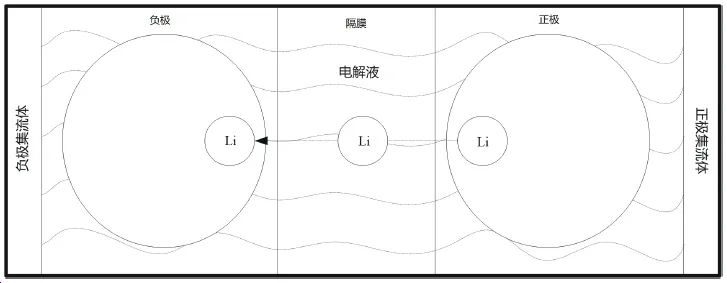
The lithium-ion battery ESP model is a simplified electrochemical model that combines the pseudo-two-dimensional model and the single particle model. The ESP model represents the positive and negative electrodes with a spherical particle, as illustrated in Figure 1.
Figure 1: Schematic of the Single Particle Model
In this model, the expression for the battery terminal voltage[3] is:
Eocv(t) represents the open-circuit voltage of the battery, determined by the open-circuit potentials of the positive electrodeUp and negative electrodeUn; thus, the expression for open-circuit voltage is:
Where:ysurf is the lithium concentration at the surface of the positive particle;xsurf is the lithium concentration at the surface of the negative particle.Up and Un have different functional expressions based on the materials used for the battery electrodes. The open-circuit potential curves for the positive and negative electrodes used in this paper are obtained by fitting experimental data[5].
The changes in lithium concentration at the positive and negative particle surfaces belong to the solid-phase diffusion process. In the P2D model, the governing equation is a partial differential equation, approximated by a three-parameter parabola to represent the lithium concentration within the solid particlesCs, while introducing the concept of average lithium concentration within the particles[6]. The surface lithium concentration can be described as:
Where:yavg is the average lithium ion concentration within the positive particle;xavg is the average lithium ion concentration within the negative particle. The governing equation is:
Where:y0 is the initial lithium ion concentration at the positive electrode;x0 is the initial lithium ion concentration at the negative electrode;I is the current, positive for discharge and negative for charge;Qp and Qn are the capacities of the positive and negative electrodes;yofs is the offset lithium concentration at the positive and negative electrodes.
Where:τp is the solid-phase diffusion time constant for the positive electrode;τn is the solid-phase diffusion time constant for the negative electrode.
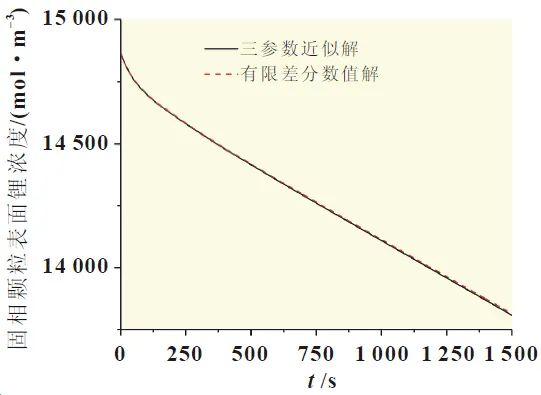
To verify the accuracy of the above simplifications, taking the negative electrode as an example, lithium ion parameters from literature[7] are selected, and the approximate calculation results of the surface lithium concentration of solid particles are compared with the numerical solutions obtained using the finite difference method for the original equation, as shown in Figure 2. Under a constant 1 C discharge, the approximate solution of the surface lithium concentration of solid particles has high precision.
Figure 2: Surface Lithium Concentration of Negative Solid Particles at 1C Discharge
As the electrochemical reactions within the battery continue, the movement of lithium ions in the electrolyte generates a potentialUcon, known as concentration polarization potential. This is primarily formed by the diffusion of lithium ions in the liquid phase, and the calculation formula is:
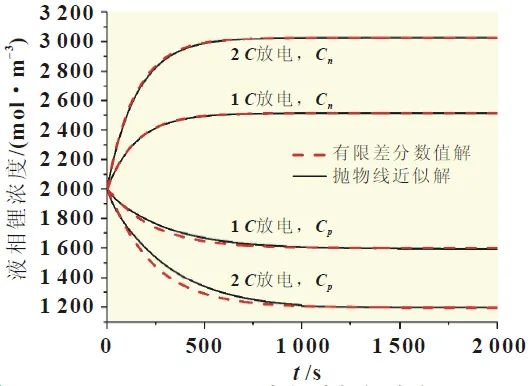
Where:R is the gas constant;T is the temperature;F is Faraday’s constant;t+ is the ion transport number;Cp and Cn are the liquid phase lithium concentrations at the positive and negative electrodes, respectively. The parabolic approximation method is used for simplified calculations of liquid phase diffusion[8]. Selecting lithium battery parameters from literature[8], the approximate calculations ofCp and Cn are compared with the numerical solutions obtained by the finite difference method for the original equation to verify the accuracy of the approximate results, as shown in Figure 3.
Figure 3: Liquid Phase Lithium Concentration at Positive and Negative Electrodes
Further simplifying Equation (6), the parameters of the positive and negative electrodes are combined, represented by the average value[8]. Therefore, the concentration polarization overpotential can be expressed as:
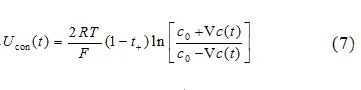
Where:c0 is the initial liquid phase lithium concentration;Δc(t) is the change in average liquid phase lithium concentration. The governing equation is:
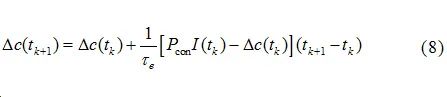
Where:τe is the liquid phase diffusion time constant;Pcon is the liquid phase diffusion coefficient.
According to the Butler-Volmer kinetic equation, the reaction polarization overpotential can be expressed as:
Where:Uact(t) is the reaction polarization overpotential;Pact is the reaction polarization coefficient.
Ohmic polarization overpotential is expressed as:
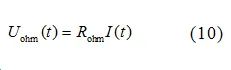

Parameter Identification and Simulation Verification
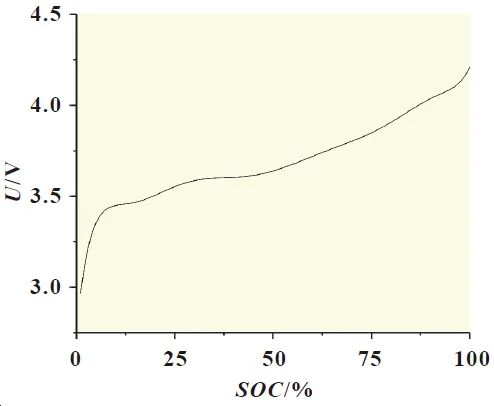
The ESP model has a total of 11 unknown parameters, among whichc0 can be provided by the battery manufacturer, while the remaining 10 parameters need to be identified. This paper conducts parameter identification in two steps. The first step involves identifying the 4 basic parameters related to open-circuit voltagey0, x0, Qp, and Qn, which can be obtained from the open-circuit potential curve. The experimentally obtained open-circuit potential curve is shown in Figure 4. Based on Equation (2), the 4 parameters related to open-circuit voltage can be obtained through fitting[3].
Figure 4: Open-Circuit Potential Curve
The second step involves identifying the remaining 6 parameters. By referring to the online identification methods in equivalent circuit models, the remaining parameters are categorized by different SOC stages, and genetic algorithms are used for multiple identifications. In this paper, the genetic algorithm generates new individuals by directly selecting the globally optimal individual for crossover and mutation with itself, simplifying the process of selecting parent individuals in traditional genetic algorithms, thereby improving the computational speed of the algorithm.
The identification program consists of two parts: the main program is the improved genetic algorithm program, and the subprogram is the fitness function calculation program. The fitness function value used in this paper is represented by the average error between the simulated output voltage of the model and the experimental voltage[5]. The smaller the fitness function value, the closer the simulated output voltage with the current parameters is to the experimental voltage, indicating better parameters.
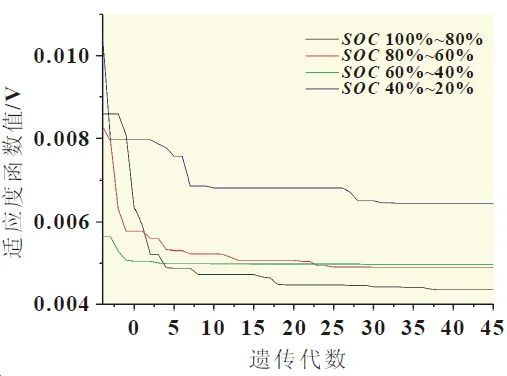
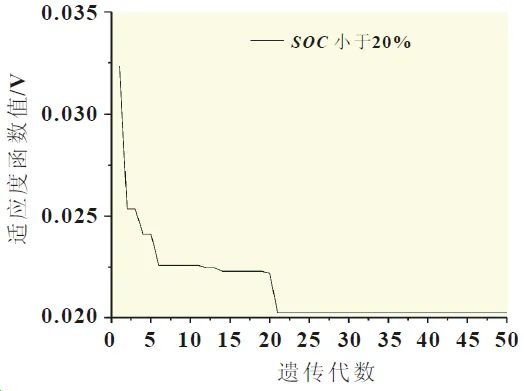
The identification program can be summarized as follows: (1) Determine the number of variables and other basic quantities, set the search range for each variable based on experience, run the main program to generate the first generation population, and input the population individuals into the subprogram to calculate the fitness function values of the current population individuals to select the optimal individuals and record them; (2) The main program selects the current globally optimal individual for crossover and mutation with itself to produce the next generation of the new population; (3) This process is repeated, and after a certain number of generations, the fitness function value gradually decreases, indicating that the optimal solutions for the variables have been found. The results of the identification program at each stage are shown in Figure 5.
(a) Calculation Results when SOC is Above 20%
(b) Calculation Results when SOC is Below 20%
Figure 5: Parameter Identification Calculation Results
As seen in Figure 5, after 50 generations of genetic iterations, the optimal individual of the population stabilizes. The parameter results at this time are the optimal solutions obtained through global search. To gain a more comprehensive understanding of the ESP model and the accuracy of the identified parameters, data with SOC below 20% were collected and parameters were identified. From the fitness function values, it can be observed that as SOC decreases, the accuracy of the identified parameters declines, especially when SOC is below 20%, where the error in the identified parameters is larger than in the previous stages. This may be due to the exacerbation of the non-linear characteristics of the battery at the end of discharge, leading to a decrease in model accuracy.
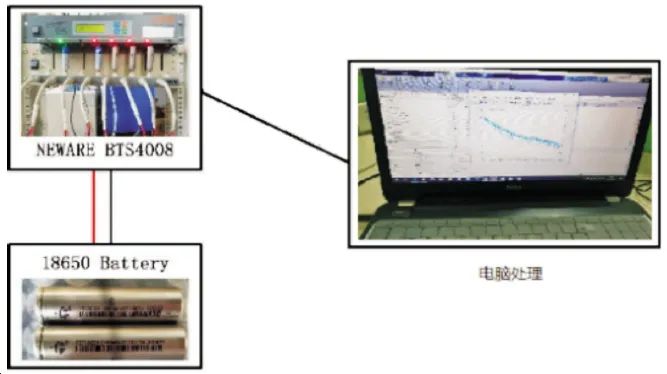
DST is a dynamic test condition designed in the US ABC Electric Vehicle Battery Testing Manual, simplified from the actual operating conditions of electric vehicles in urban environments, reflecting the dynamic performance of the battery under instantaneous large current shocks and rapid switching between charging and discharging. To better understand the accuracy of the obtained parameters, the DST condition current is used as input data, and the simulated output voltage is compared with the experimental values. As shown in Figure 6, the experimental equipment used was the New Wei Battery Testing System, and the battery used was an 18650 ternary lithium battery with a maximum cutoff voltage of 4.2 V and an operating voltage of 3.6 V.
Figure 6: Experimental Equipment Diagram
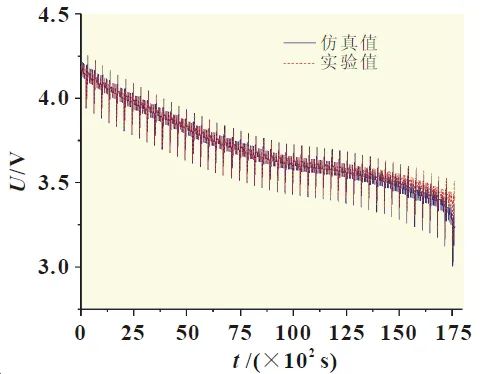
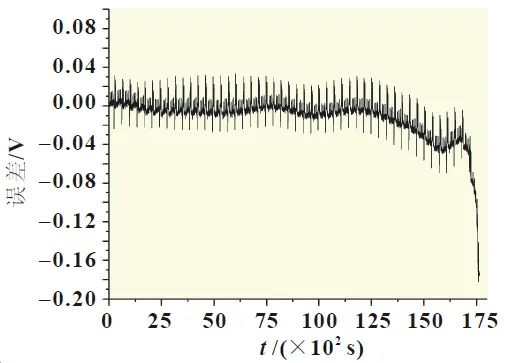
Under the DST discharge condition, the simulated terminal voltage, experimental values, and errors are shown in Figure 7. After applying periodic DST condition currents, the voltage across the battery exhibits significant periodic dynamic changes. The ESP model accurately reflects this phenomenon; during the period from 0 to 15,000 seconds, the model’s accuracy is best, with a maximum error of about 0.03 V, and most errors do not exceed 0.02 V; after 15,000 seconds, the model’s accuracy begins to decline, at which point the battery’s SOC is approximately below 20%. Particularly after 17,000 seconds, the error increases significantly, with a maximum error reaching 0.18 V, which is due to the non-linear characteristics of the battery at the end of discharge causing the model to no longer accurately describe the battery state, consistent with the phenomena observed in the previous parameter identification.
(a) Simulated Terminal Voltage and Experimental Values
Figure 7: DST Condition Discharge Data

Battery State of Charge Estimation
This paper establishes an adaptive strong tracking Sigma point Kalman filtering algorithm (ASTSPKF) based on the Sigma point Kalman filter (SPKF) by combining it with a strong tracking filter and introducing an adaptive covariance matching method for real-time estimation of noise covariance.
The system’s state variables are set as follows:
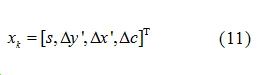
Where:s represents SOC, and the control equation for s is determined by the ampere-hour integration method, while the control equations for the other three variables are determined by Equations (5) and (8). The system state equation is[9]:
Where: Δt is the system sampling time;η is the coulombic efficiency;wk is the system observation noise;ik is the system input. The system measurement equation is:
Where:vk is the system measurement noise, and the specific expression of the measurement equation is determined by Equation (1).
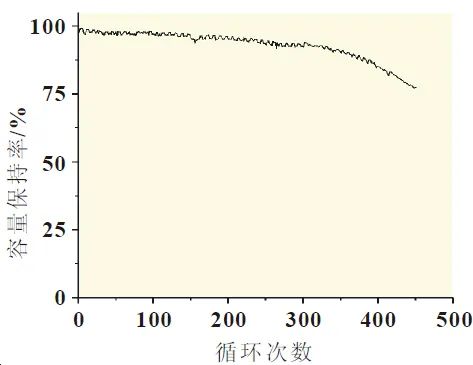
For the coulombic efficiency η, it is generally taken as 1 in standard calculations. In this paper, an aging coefficient λ is introduced through cyclic discharge experiments, which is multiplied by η to correct the model state equation. The aging coefficient is fitted using a polynomial, and the experimental curve used for fitting is shown in Figure 8.
Figure 8: Battery Cycling Curve
SOC estimation algorithm implementation specific steps are as follows:
(1) Initialization, set the initial state vector X0 and covariance P0; (2) Generate the Sigma points at time k−1 based on the unscented transform (UT) and the state vector at time k−1, calculate xi (i=0, …, 8); (3) Time update, update the state vector one step Xi, k|k−1 through weight calculation, obtaining the system’s prior estimate and prior estimate error covariance; (4) Strong tracking filtering, realized by adding a diminishing factor to the system’s prior estimate covariance matrix to achieve the strong tracking characteristic of the filter, the diminishing factor μk calculation steps are[10]:
Where:k is the time;εk represents the residual sequence, which is the difference between the measurement data at time k and the measurement data at time k−1; Vk is the covariance matrix of the residual sequence;ρ is the forgetting factor, generally taken as 0.95.
Where:Hk is the measurement matrix;Qk−1 is the system process noise;Rk is the system measurement noise. The calculation formula for the prior estimate error covariance at this time should be:
(5) Measurement update, obtain the mean and covariance of the measurement prediction values through weighted unscented transformation; (6) Correct the system state estimate based on the sum, calculate the joint prior covariance, then calculate the Kalman filtering gain Kk, and correct the system state Xk and covariance Pk using Kk and the voltage measurement values.
Introduce adaptive methods to update the system noise in real time. The calculation of system noise under adaptive methods is:
Where:M is the size of the variance window;ek is the error between the estimated value and the measurement value at time k;n is the dimension of the variable;wc is the covariance weight of the Sigma sampling points;Kk is the Kalman gain at time k. The remaining basic formulas omitted in the Sigma point Kalman filtering process can be referenced in literature[10].
The ASTSPKF algorithm flowchart is shown in Figure 9.
Figure 9: ASTSPKF Algorithm Flow
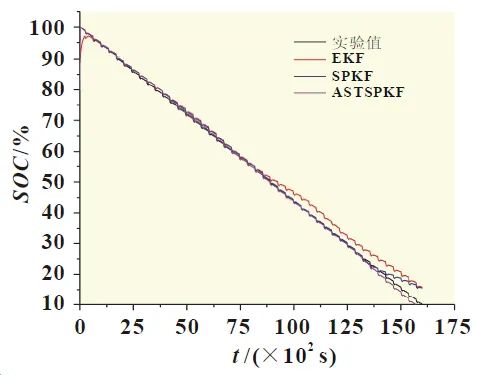
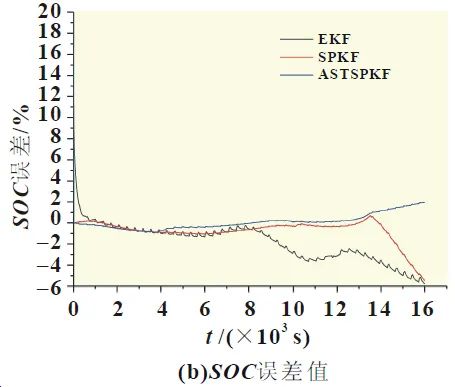
Using the DST condition current as input data, the SOC estimation simulation results are obtained and compared with experimental values, as shown in Figure 10. EKF indicates the SOC calculated using the extended Kalman filtering algorithm; SPKF indicates the SOC calculated using the Sigma point Kalman filtering algorithm; ASTSPKF indicates the SOC calculated using the adaptive strong tracking Sigma point Kalman filtering algorithm, aiming to study the correction ability of each Kalman filtering algorithm on the estimated values, with the initial SOC set to 0.8.
(a) SOC Simulation Results and Experimental Values
Figure 10: SOC Simulation Results and Experimental Values under DST Conditions
As seen in Figure 10, after using the Kalman filtering algorithm, the SOC estimates return to the normal range within a short time, with EKF taking the longest time, while the other two algorithms complete corrections within seconds. This is due to Kalman filtering providing feedback corrections to the estimated values through the Kalman gain. In terms of estimation, all three algorithms can track the SOC values, especially when SOC is above 45%, where the estimation errors of each algorithm are similar, all within 2%; as SOC decreases, the EKF estimates first exhibit significant fluctuations, and when SOC is below 20%, the accuracy of SPKF estimates also begins to decline. ASTSPKF shows the best estimation performance, with a maximum error of 2.3%, and most errors within 1%.
The lowest estimation accuracy of EKF is due to its linearization of the system using first-order Taylor expansion, which is generally only suitable for weakly non-linear systems. SPKF achieves updates of system states and error covariances through UT transformation, achieving a precision that can reach fourth-order accuracy of Taylor series, thus its estimation accuracy is next. Based on SPKF, the introduction of a strong tracking filter can reduce the weight of previous measurement values in calculations, enhancing the weight of new measurement values, improving tracking ability on estimated values, and the introduction of noise adaptive filtering can reduce filtering failures caused by inaccurate fixed noise settings, further improving accuracy, hence ASTSPKF achieves the highest precision. However, the methods used in this paper are model-based SOC estimations, and the advantages and disadvantages of the algorithms used can affect the estimation accuracy to a certain extent. Ultimately, as the model error increases, the SOC estimates inevitably exhibit increased errors. Overall, the ASTSPKF algorithm established in this paper can accurately estimate SOC based on the ESP model.

Conclusion
This paper conducts parameter identification based on the extended single particle model, combined with an improved genetic algorithm, based on battery discharge experiments, then simulates programming and compares with operational experiments to validate accuracy. The ASTSPKF algorithm is employed to estimate SOC based on the established model, and results indicate that the strong tracking filter and adaptive filtering methods enhance the estimation tracking capability of the Kalman filtering algorithm, and to some extent reduce the impact of model accuracy on the estimated values, but the accuracy of the estimates ultimately decreases as model errors increase.
References:
[1] DOYLE M, FULLER T F, NEWMANJ. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertioncell[J]. Journal of the Electrochemical Society, 1993,140(6):1526-1533.
[2] LUO W, LYU C, WANG L,et al. A new extension of physics-based single particle model for higher charge-dischargerates[J]. Journal of Power Sources, 2013, 241: 295-310.
[3] Zheng Jun. Parameter acquisition and aging analysis of lithium-ion batteries based on improved single particle model[D]. Harbin: Harbin Institute of Technology, 2015.
[4] Xu Xing, Wang Wei, Chen Long, et al. Parameter identification of lithium-ion battery electrochemical model based on GA[J]. Automobile Engineering, 2017, 39(7): 813-821.
[5] Ma Kehua. Parameter acquisition and variable parameter model of lithium-ion batteries[D]. Harbin: Harbin Institute of Technology, 2014.
[6] TING S, CHAO L, WEILINL, et al. The validation of approximate model for lithiumion solid phasediffusion under operating conditions[C]// 2012 7th International PowerElectronics and Motion Control Conference (IPEMC 2012). China: IEEE, 2012: 177-181.
[7] Sun Ting. Research on lithium-ion battery model simulation and parameter identification[D]. Harbin: Harbin Institute of Technology, 2012.
[8] LUO W, LYU C, WANG L,et al. An approximate solution for electrolyte concentration distribution inphysics-based lithium-ion cell models[J]. Microelectronics Reliability, 2013,53(6): 797-804.
[9] Liu Xuan. Research on charging strategy of lithium-ion battery pack based on improved single particle model[D]. Harbin: Harbin Institute of Technology, 2016.
[10] LI D, OUYANG J, LI H,et al. State of charge estimation for LiMn2O4 powerbattery based on strong tracking sigma point Kalman filter[J]. Journal of PowerSources, 2015, 279: 439-449.
Authors: Wu Bo, Xie Feng, Lu Peihang, Xu Jinli
Affiliation: School of Mechanical and Electrical Engineering, Wuhan University of Technology

Scan to add the group owner and indicate unit + name
Join the exclusive battery industry chain WeChat group of Battery China Network
Battery China Network Related Business Contact
Media Promotion Consultation
Contact: Ms. Wu
Phone: (86)18611555116 (same WeChat number)
Email: [email protected]
Submission Consultation
Contact: Mr. Yan
Phone: (86)18515816697 (same WeChat number)
Email: [email protected]
Research Report Consultation
Contact: Mr. Zhou
Phone: (86)18910499049 (same WeChat number)
Email: [email protected]
Industry Conference Consultation
Contact: Mr. Zhou
Phone: (86)18910499049 (same WeChat number)
Email: [email protected]
Contact: Mr. Wu
Phone: (86)13269999859 (same WeChat number)
Email: [email protected]