The core of solid-state physics is band theory, which classifies the crystalline world into two categories: “insulators” and “conductors”. Then, to fill in the gaps for semiconductor applications at room temperature, the concept of “semiconductors” was added. This is now common knowledge taught in high schools, marking the establishment of band theory.^_^.
Of course, band theory is great; within its framework, many new physics can be incorporated, from perturbation theory to magnetism, electron correlations, and spin-orbit coupling (SOC). This layered approach has achieved great success. In this sense, solid-state physics or condensed matter physics has endured and benefited a wide audience, with the concepts, images, and related physics of bands being a model for materials science.
Today, beyond correlated physics, band theory is moving towards the necessity of including SOC, demonstrating its increasingly important role in condensed matter physics, especially in quantum materials. Specifically, several rough impressions can be highlighted:
Strong Spin-Orbit Coupling (SOC)
(1) Strength: SOC is related to atomic number; the heavier the ion, the stronger the SOC, which is common knowledge. Therefore, as research on transition metal compounds shifts from 3d to 4d and 5d, the most notable new physics observed is the mixing of SOC, although orbital expansion is also significant. This complexity of correlated physics is further complicated by the inclusion of SOC, making the condensed matter of 4d/5d compounds even more intricate. To this day, this remains a state of “high mountains and flowing water, difficult to find a kindred spirit”.
(2) Magnetism: Although it is known that the origin of magnetic anisotropy is SOC, understanding it phenomenologically is more intuitive. Spin interactions transition from the Heisenberg’s spin dot product to the spin cross product, introducing pseudovectors physically, and new elements such as anisotropy, surface Rashba, DM interactions, and spin frustration emerge. Here, SOC is the physics of spin cross products. Because of the cross product, the Hamiltonian for magnetism suddenly becomes complex. For example, the seemingly dizzying LLG equation system, due to the appearance of energy terms with two or three consecutive cross products, can drive one mad. Therefore, it is needless to say that the many years of neglect in Ising’s treatment of multiferroic physics can hardly be discussed without SOC.
(3) When condensed matter transitions from symmetry breaking to topological quantum states, the core physics is also SOC.Ising conjectured that spin cross products are the “phenomenological” roots of overlap and transformation in band space, thus SOC can essentially be equated with topological nontriviality. Amen!
The above three points are complex, with many variants and areas requiring deep exploration. Each point is merely a simplification for outsiders’ understanding. For now, let’s look at some simpler derivations. After consulting Professor Lu Chengliang from Huazhong University of Science and Technology, Ising initially understood that SOC has a well-known effect on band structure, which is the Jeff =1/2 state, known as the effective spin 1/2 state. When examining the energy levels of transition metal insulators, crystal fields lead to the splitting of t2g and eg orbitals, and if SOC is added, it may induce an Jeff= 1/2 and/or Jeff = 3/2 state in the energy levels. Here, Jeff = 1/2 has special significance: (1) Magnetic physics becomes simpler; those electrons with slightly lower energy levels can be temporarily disregarded, focusing only on the Jeff = 1/2 spin state closest to the Fermi level.(2) The 1/2 spin is, of course, closer to quantum, thus allowing quantum spin physics to come alive in magnetic systems that should be treated as classical large spins.(3) Due to the introduction of cross products by SOC, and because of the 1/2, the spin frustration effect also becomes significant. More could be listed, but that exceeds Ising’s knowledge limits.
Alright, this physical derivation essentially limits our focus to 4d/5d systems. Their atoms are heavy, SOC is strong, and the d orbitals of these ions are quite extended, leading to a relatively weaker correlation strength compared to 3d systems, thus forming a three-dimensional space of “Heisenberg interaction J – correlation strength U – SOC strength”. Alas, no more talk; the complexity and richness of this 4d/5d system, even strong scholars like Professor Gang Cao from the University of Colorado would be “worn out for her”, hence his cool physique.^_^.

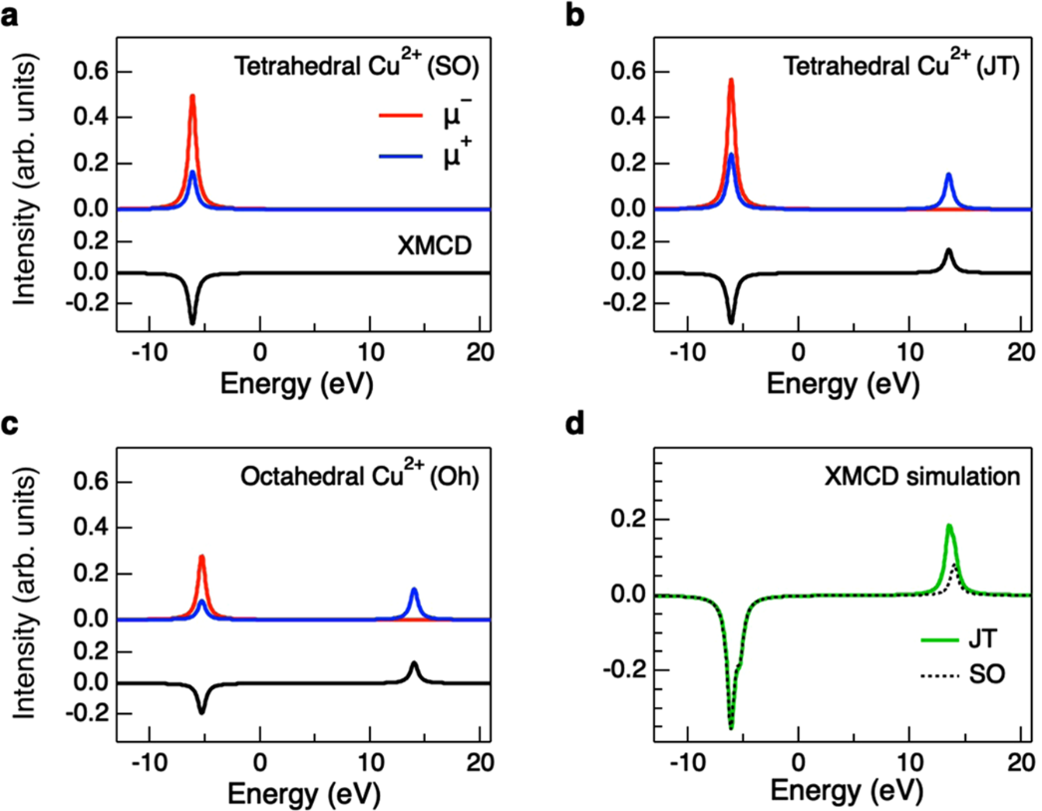
Schematic illustration on the t2 splitting of tetrahedral Cu2+ due to the Jahn-Teller effect (left) and spin-orbit coupling (right).
OK, are there exceptions? Or more specifically, is it absolutely impossible to achieve strong SOC in 3d compounds? There are some recent studies that seem to show hope, exciting us to ponder and gain new knowledge and achieve new utilities.
The situation arises from some 3d Co2+ and Cu2+ oxides. These ions are located at octahedral or tetrahedral coordination centers, forming a layered honeycomb crystal structure that closely resembles the anisotropic and bond-dependent exchange coupling depicted in the Kitaev model, making them potential candidates for quantum spin liquids. As expected, analyzing the energy level structure of these systems seems to indicate the presence of the Jeff = 1/2 characteristic, suggesting that strong SOC might also exist in 3d systems! Otherwise, how could this Jeff = 1/2 ground state form?
A specific material leading to the Jeff = 1/2 physics in the 3d system is CuAl2O4, where Cu2+ occupies the A site. Theoretical calculations predict that this system is a spin-orbital-entangled Jeff = 1/2 Mott insulator, although Ising believes that Cu2+ itself is an S = 1/2 ion. Perhaps because there were only computational results without empirical evidence, such a “against common sense” result was ultimately published in PRB rather than PRL. Subsequently, some structural analyses confirmed that this system does not exhibit significant structural distortion or lattice symmetry breaking.
Thus, the physical origin of Jeff = 1/2 becomes unclear, leading many to wonder: is this Jeff = 1/2 truly a product of SOC?
How to answer this Yes or No? Professor Huang Di-Jing’s team from the Hsinchu Synchrotron Radiation Center, along with colleagues from Tsinghua University and National Yang Ming Chiao Tung University in Hsinchu, as well as collaborative teams from Japan’s NIMS, Waseda University, and Russia, utilized their synchrotron radiation center’s resonant inelastic X-ray scattering (RIXS) to address this issue. Among them, A. Fujimori, C. T. Chen, and S. V. Streltsov are all well-known scholars.
Synchrotron radiation + RIXS, besides extracting crystal structure information, can also accurately measure and fit crystal field data and the strength of SOC, with high sensitivity to anomalous spin excitations. As for the underlying mechanisms, specialized knowledge is required, and Ising does not understand much, so I will not “sell melons” here.
The results obtained by Professor Huang’s team were indeed somewhat unexpected. The main insights can be summarized in two simple sentences: In CuAl2O4, the tetrahedral structure (with Cu2+ at its center) exhibits strong local Jahn-Teller distortion, while the so-called SOC strength is not significant. It is precisely this distortion that leads to the appearance of the Jeff = 1/2 state, correcting our “illusion”—that there truly exists strong SOC in this CuAl2O4.
Indeed, SOC in the 3d system is not absent; it exists and can contribute significantly, just like in multiferroic compounds. Of course, because it is not strong enough, the second type of multiferroics is still on the long march. Professor Huang Di-Jing’s work did not produce any giant effect, nor did it reveal any unprecedented original innovation; it merely corrected some of our “excessive expectations”. However, such work addresses cutting-edge scientific questions, employing unique techniques to tackle difficult issues, clarify facts, and sort out problems. This should be one of the research styles appreciated by npj QM. In the future, we can further explore this ambition; isn’t that our mission and destiny as physicists?!
Unwavering conclusion: Ising is an outsider; if misunderstood, please forgive. Those interested can visit the original text. Original link:
Resonant inelastic X-ray scattering as a probe of Jeff = 1/2 state in 3d transition-metal oxide
H. Y. Huang, A. Singh, C. I. Wu, J. D. Xie, J. Okamoto, A. A. Belik, E. Kurmaev, A. Fujimori, C. T. Chen, S. V. Streltsov & D. J. Huang
npj Quantum Materials volume 7, Article number: 33 (2022)
https://www.nature.com/articles/s41535-022-00430-0
卜算子·人间四月
物自曙华生,绿向清明借
瘦水阑声落影依,乍暖犹寒夜
停步欲端详,俯目凌波谢
历遍人间躁动新,四月风情惹

Note:
(1) Editor Ising, affiliated with the School of Physics at Nanjing University, also serves as an editor for npj Quantum Materials.
(2) The image at the bottom shows the scene of Xuanwu Lake at the transition from spring to summer in April (20200412), featuring various meteorological elements, similar to how this Jeff = 1/2 state can arise from different meteorological conditions. The small poem also carries this meaning.
(3) The cover image illustrates an important application of these Jeff = 1/2 systems: quantum spin liquids. From http://www.sci-news.com/physics/quantum-spin-liquid-new-quantum-state-matter-03754.html. The first image regarding spin-orbit coupling comes from https://opli.net/media/10225/spin-orbit-coupling-of-atom-qubits-dec-img.jpg.
Selected Articles
Gate-Controlled Two-Dimensional Quantum States
CsV3Sb5– Revealing the Depths
HfO2‘s Journey and Markings
Non-Point “Measurement” Topology, “Magneto-Optical” Ruthenium Chloride
Topology Causes Dust, Heroes with Magnetism
Quantum Oscillation Smooths the Lake
Two-Dimensional Magnons Blooming
Caged Birds Also Have Spring
Exploring Thunder in the Shadow
Countless Sceneries Hang by a Thread
Welcome to subscribe to npj Quantum Materials‘s Email Alerts
Click https://idp.nature.com/register/natureuser to complete your free subscription
