Key Elements and Module Combination Paths for Elementary Math Reasoning Activities

Key Elements and Module Combination Paths for Elementary Math Reasoning Activities

Song Yuyang

Abstract: The awareness or ability of reasoning is one of the main manifestations of students’ mathematical thinking in the compulsory education stage. Conjecturing, reasoning, and exemplifying are not only important elements of the performance level of reasoning awareness but also core activities in the reasoning learning process. The core activity design elements and module combination paths mainly include the types, elements, and driving forces of conjecture-specific activities; the goal progression, discourse system, and performance dimensions of reasoning-specific activities; the materials, methods, and organization of exemplifying-specific activities; the module combination paths and paradigms of conjecturing, reasoning, and exemplifying activities; and five major strategies for multiple reasoning learning paths based on teaching differences in a single lesson.

Keywords:“Compulsory Education Math Curriculum Standards (2022 Edition)”Reasoning AwarenessConjectureReasoningExemplification

The awareness or ability of reasoning is one of the main manifestations of mathematical thinking in the compulsory education stage. Reasoning awareness can be seen as the initial stage of reasoning ability, and the development of reasoning awareness can promote students’ preliminary formation of mathematical thinking methods, laying an experiential foundation for the development of reasoning ability. The reasoning awareness in the “Compulsory Education Math Curriculum Standards (2022 Edition)” mainly manifests in three types of activities: first, conjecturing, which is “knowing that one can start from some facts and propositions, and deduce other propositions or conclusions based on rules” and “being able to conjecture or discover some preliminary conclusions through simple induction or analogy”; second, exemplifying, which is “being able to conjecture or discover some preliminary conclusions through simple induction or analogy”; and third, reasoning, which is “providing reasonable explanations for one’s own and others’ problem-solving processes”. Conjecturing, reasoning, and exemplifying are not only important elements of the performance level of reasoning awareness but also core activities in the reasoning learning process. Conjecturing is the key and core of reasonable reasoning, a specific method and necessary link of reasonable reasoning. The proposal of conjectures summarizes the reasoning thinking process and refines the content of reasoning thinking, providing opportunities for mathematical discoveries and exercising mathematical thinking. “Conjecture-Verification” is the basic path of reasonable reasoning, where verification refers to the process of explaining and confirming conclusions based on mathematical facts, using mathematical language in a justified and logical manner, which is a comprehensive application of reasoning and exemplification. Here, the basis of mathematical facts is exemplification, and logical expression and explanation are reasoning activities.

The development of elementary math reasoning awareness requires strengthening practical research on conjecturing, reasoning, and exemplifying, categorizing activity types, processes, organizational forms, and applicable scopes, designing activities and module combinations in conjunction with lesson examples, forming paradigms for specialized and comprehensive activity designs, and refining operational design strategies.

Types, Elements, and Driving Strategies of Conjecture-Specific Activities

1. Types and Elements of Conjecture Activities

Based on the classification of reasonable reasoning, conjecture activities are divided into three types: inductive conjectures, analogical conjectures, and intuitive conjectures; based on the content direction of conjectures, conjectures can also be divided into those directed towards exploring conclusions, methods, and processes. As shown in Figure 1, there are mainly two routes for conjecture activities.

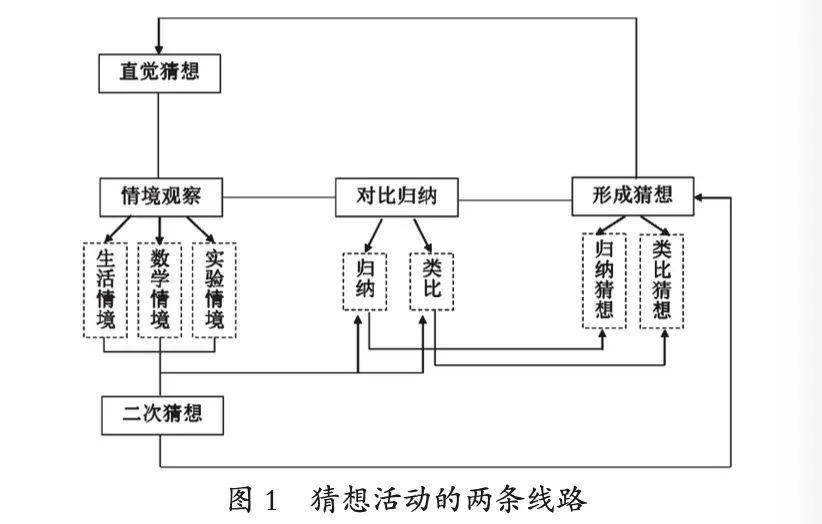
Route 1: Situational Observation—Comparative Induction—Forming a Conjecture; Route 2: Intuitive Conjecture—Situational Observation—Secondary Conjecture. Here, situational observation is a necessary activity for both activity routes, which includes three types of situational observations: life situational observation, mathematical situational observation, and experimental situational observation. Under situational stimuli, students engage in comparative induction, which includes both induction and analogy activities. Situations and problems are two key elements in the design of conjecture activities; the situation is the starting point of conjecture, supporting conjectures through situational stimuli; problems play a crucial guiding role in the direction of conjectures, forming conjectures. Therefore, the design of conjecture activities mainly focuses on situation design and problem design, forming corresponding situational and problem-driven strategies.

2. Situational Driving Strategies

Situational driving strategies refer to helping students propose conjectures through situational drives, summarizing the reasoning thinking process and refining the content of reasoning thinking, providing opportunities for mathematical discoveries and exercising mathematical thinking. Situational driving includes life situational drives, mathematical situational drives, and experimental situational drives, each supported by life experiences, knowledge associations, and experimental operations.

Life situational drives start from the characteristics of textbook content and the age characteristics of students, designing vivid, interesting, and intuitive life situations that activate students’ existing life experiences to generate mathematical conjectures. For example, in the conjecture activity of the “boat rental problem,” students activate their “saving money” experience in the life situation of renting a boat to make conjectures about the optimal solution.

Mathematical situational drives create mathematical situations using the rules, laws, and properties in the textbook, supporting conjectures through comparative observations, examples, and finding connections. For example, in the conjecture activity of the “99 or 999 multiplied by a one-digit number” rule, the first group of calculations is provided to organize students to explore the rule and apply it to write the answers to the subsequent two questions: “99×1=99, 99×2=198, 99×3=297, 99×4=396… 99×7=99×8= “; then the second group of calculations is provided: “999×1=999×2=999×3=999×4= “, asking students to conjecture the answers to the second group of calculations based on the rules of the first group of calculations and verify them.

Experimental situational drives visually and intuitively present the knowledge exploration process and results through experimental operations, prompting students to make reasonable conjectures. For instance, the derivation of the cone volume formula can use experimental situational drives for conjecturing: (1) Recall and associate: How was the cylinder volume formula derived? What is the relationship between the cylinder and the rectangular prism before and after transformation? Present a rectangular prism, a square prism, and a cylinder, and discuss: When studying the volume of the cone, which shape would you choose for research? (2) Experimental conjecture (I): Use the “water pouring method” experiment where the cone pours water into the cylinder to conjecture the volume relationship between the cone and the cylinder; (3) Experimental conjecture (II): Use the “water displacement method” experiment where the cylinder and cone are immersed in a rectangular water tank to conjecture the volume relationship between the cone and the cylinder.

3. Problem-Driven Strategies

Problem-driven strategies focus on helping students clarify the background and causes of conclusion generation through problem drives, provoking student inquiry and forming conjectures. Problem-driven strategies mainly include conclusion-directed problem drives, process-directed problem drives, and method-directed problem drives.

Conclusion-directed problem drives refer to emphasizing knowledge results in problem design, making conclusions clear, starting with the end, allowing students to make purposeful conjectures. In learning the “basic properties of proportions,” students first recall the basic properties of proportions and then present four proportions: 2:1=3:1.5, 0.2:2.5=8:100, organizing students to observe calculations and discuss: What is the relationship between the inner and outer terms of the proportion? Under the guidance of this conclusion-directed problem, students form the conjecture: In proportions, the product of the two outer terms equals the product of the two inner terms.

Process-directed problem drives focus on the specific methods and processes to obtain results, designing a series of process-oriented thinking problems to gradually help students form conjectures. When exploring the rule of “two-digit numbers multiplied by 11,” students can observe calculations and answers, guiding them through a series of questions to observe, think, and propose conjectures. Present the calculations: 31×11, 41×11, 62×11, 53×11, and ask students to guess what patterns might exist in the products of two-digit numbers multiplied by 11, and why such patterns exist, thereby forming a complete conjecture about “two-digit numbers multiplied by 11”.

Method-directed problem drives utilize the connections between prior knowledge to facilitate transfer, using problems to guide and transfer applications to form conjectures. For example, when studying the characteristics of multiples of a number, students first identify the pattern of multiples of 10, organizing them to observe and discuss, forming the conjecture: The unit digit of multiples of 10 is always 0, and validating this with examples; next, they transfer the method to find the characteristics of multiples of 5, leading students to conclude: The unit digit of multiples of 5 is either 0 or 5; finally, organize students to review how they conjectured the features of multiples of 10 and 5, guiding them to conjecture the characteristics of multiples of 2, 3, 4, and 6. This process demonstrates the transfer and application of the conjecturing methods for the characteristics of multiples of 10 and 5.

Goals Progression, Discourse System, and Performance Dimensions of Reasoning-Specific Activities

1. Establishing Goals Progression for Reasoning-Specific Activities

Elementary math reasoning-specific activities need to establish a goals progression of “be able to speak—be good at speaking—be able to debate” based on the characteristics of the learning stage. That is, in the first stage, the requirement is to “speak completely” and “speak accurately”; in the second stage, the requirement is to “speak simply and clearly” and “express in an organized manner”; in the third stage, the requirement is to “explain and illustrate one’s viewpoints based on evidence” and “question and refute others’ ideas”.

2. Improving the Discourse System for Reasoning-Specific Activities

Improving the commonly used discourse system is an important aspect of reasoning-specific activities. The commonly used discourse system for reasoning generally consists of four parts: logical language vocabulary, common reasoning sentence patterns, symbolic language, and visual representation. Logical language vocabulary includes sequence relation conjunctions like “first, second, third,” comparative relation conjunctions like “also,” and progressive relation conjunctions like “or” and “at the same time”; common reasoning sentence patterns include syllogisms like “because…, and also…, therefore…”; symbolic language includes expressions like “38<40, 40×5=200, 38×5<200”; visual representation includes geometric intuition, intuitive judgment reasoning, and transformation between texts and images. For example, in the “comparison” section, it is important to clarify the reasoning comparison process, which requires support from discourse systems such as “because 92>90, and also because 90×8=720, therefore 92×8>700”.

3. Characterizing the Performance Dimensions of Reasoning-Specific Activities

“Reasoning,” “writing reasoning,” and “debating reasoning” are the three performance dimensions of reasoning-specific activities, requiring comprehensive characterization. Reasoning activities should focus on the choice of “positive reasoning and negative denial” paths. Positive reasoning is suitable for correct propositions, using standardized sentence patterns such as “because… and also… therefore…”; “first… second… third… last…” to make complete and logical statements, gradually forming good reasoning skills. Negative denial is suitable for judgment-type propositions, overturning the meaning of the proposition statement through a counterexample. For the knowledge point “2 is a prime number,” many propositions can be designed, such as “all primes are odd numbers, all composites are even numbers”; “the sum of two different primes must be even”; etc. These types of questions can use examples and negative reasoning to deny the validity of the propositions.

Writing reasoning activities refer to recording the reasoning process in a complete manner using written explanations, usually expressed using the three-part reasoning discourse system of “because… and also… therefore…”. Debating reasoning activities should grasp the nodes of debate, leveraging the advantages of debate at points of knowledge confusion and method optimization. When students have disagreements about understanding knowledge or choosing problem-solving methods, they can organize debates around points of knowledge confusion and method optimization, achieving a deep understanding of knowledge through debate and developing higher-order thinking. When debating concepts, it is important to capture the essence of the concept; when debating methods, the focus is on showcasing the advantages of each method and creating a collision of ideas, leading one side to be convinced by the other’s viewpoint.

Materials, Methods, and Organization of Exemplification-Specific Activities

In the exemplification process, various versions of textbook examples and exercises can be compared to enrich the types and quantities of material evidence, providing students with diverse exemplification materials. For example, in the lesson on the “multiplication distribution law,” the People’s Education Edition, Zhejiang Education Edition, and Beijing Normal University Edition each have their strengths in the choice of exemplification materials, allowing for comparative analysis and reasonable selection to carry out reasoning exemplification activities. In terms of the quantity of exemplification, the Zhejiang Education Edition derives four equations from four examples, then guides students to imitate and exemplify before proceeding to summarize symbolically, reflecting the process of incomplete inductive reasoning. In terms of the richness of exemplification types, the People’s Education Edition includes implicit multiplication distribution laws in mental multiplication; the Beijing Normal University Edition emphasizes geometric intuition, with examples in figures, exercises, and accompanying practice that discover multiplication distribution laws, also interspersing explanations of multiplication meanings using several instances, demonstrating the richness of exemplification materials.

Based on the characteristics of exemplification content, various exemplification methods can be selected. Exemplification methods mainly include listing multiple positive examples for incomplete inductive reasoning, listing a counterexample to deny a conclusion, and conducting scientific argumentation based on a single example. Inductive reasoning activities should go through the process of “conjecturing—verifying—drawing conclusions”. After conjecturing, individual examples can first be presented; once the types and methods of exemplification are clarified, each student can present two or three examples, which are then summarized to draw conclusions from incomplete inductive reasoning, followed by the process of finding counterexamples to cultivate a scientific attitude towards exemplification. After drawing conclusions from incomplete inductive reasoning, scientific argumentation can be used to explain the origins, achieving a perfect combination of inductive and deductive reasoning. For example, after drawing conclusions about the characteristics of multiples of 2, 3, and 5 using incomplete inductive reasoning, organize activities to explain the origins: since both 2 and 5 are factors of 10, excluding the unit digit, the remaining number is a multiple of ten, so it must be a multiple of 2 or 5; for the characteristics of multiples of 3, small stick diagrams can be used to illustrate that the digits in each position represent the number of sticks remaining after taking multiples of 3.

The organization of exemplification-specific activities should fully integrate various activities such as student presentations, exploratory assignments, and writing math papers to enrich the types of reasoning exploration. The organization of presentation activities can combine daily training with competitive displays; the organization of exploratory assignments can combine independent assignments with exhibition activities; writing math papers can combine independent writing with peer review and publication. Through various types of organizational methods, students’ diverse reasoning activities can be showcased and promoted based on solid training. Presentation content can be divided into homework presentations and specialized presentations. Homework presentations focus on the difficulties and key points in classroom and homework assignments, using in-class presentations and video recording for daily training, engaging in interactive evaluations of presentation outcomes, helping students accumulate presentation experience, gradually forming presentation steps and models. Specialized presentations can involve specifically selecting certain types of problems for students to engage in presentation activities, such as conceptual understanding, algorithm explanation, and measurement themes. The organization of presentations should be diverse, employing a progressive approach of “daily training—school-level evaluation—district-level display,” allowing students to accumulate experience in daily training, stimulating interest in presentations through evaluations and displays, establishing presentation role models, and forming presentation patterns. Writing math papers should go through the stages of “finding topics—designing reasoning—writing documents,” with each stage closely tied to reasoning elements. After students complete independent writing, they should engage in peer-to-peer and teacher-student exchanges for improvement, and outstanding works can participate in math paper competitions or be submitted for publication in public journals, fully mobilizing students’ enthusiasm.

Students will experience diverse exemplification materials, methods, and activities from different perspectives, helping them accumulate richer exemplification experiences and promoting the development of reasoning awareness.

Module Combination Paths and Paradigms for Conjecturing, Reasoning, and Exemplifying Activities

The design of comprehensive reasoning activities can combine conjecturing, reasoning, and exemplifying activity modules based on different types of reasoning, developing various learning paths and providing comprehensive activity paradigms.

1. Inductive Reasoning Comprehensive Activity Module Combination

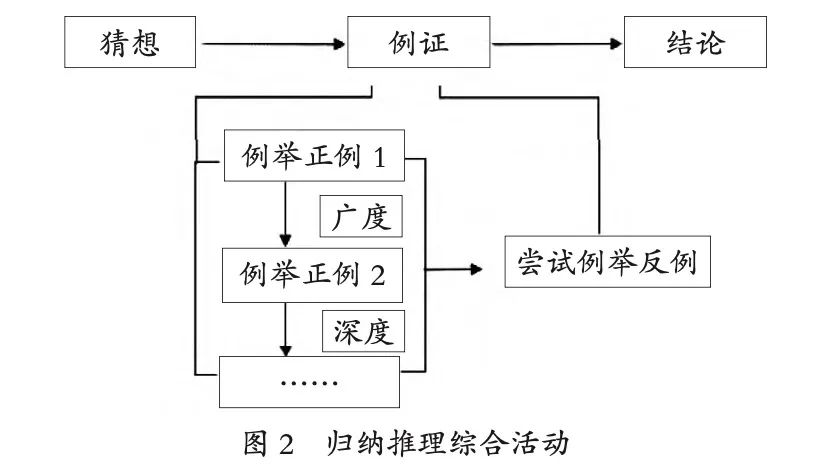
Inductive reasoning comprehensive activities mainly include three modules: conjecturing, exemplifying, and concluding. Among them, exemplification is the central link, consisting of positive and negative exemplification. As shown in Figure 2, first, use positive examples for verification, focusing on the breadth and depth of examples; then, attempt to list counterexamples to draw conclusions.

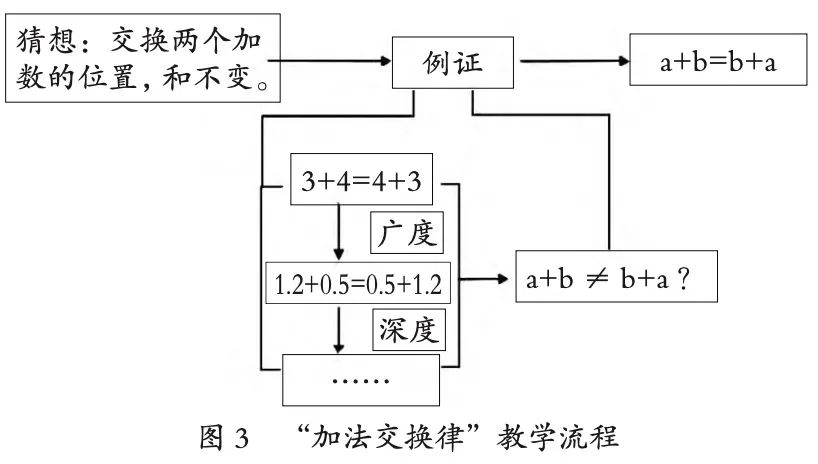
For example, in the lesson on the “commutative law of addition,” the process of the inductive reasoning comprehensive activity is shown in Figure 3. Step 1: Trigger conjecture. First, based on existing materials, trigger the conjecture: swapping the positions of two addends does not change the sum. Step 2: Exemplification explanation. Attempt to provide positive examples, presenting integer addition, decimal addition, and fraction addition, reflecting breadth and depth; then attempt to provide a counterexample where swapping the addends leads to an unequal sum, which cannot be found. Step 3: Confirm conclusion. Inductively conclude that a+b=b+a, revealing the commutative law of addition.

2. Analogical Reasoning Comprehensive Activity Module Combination

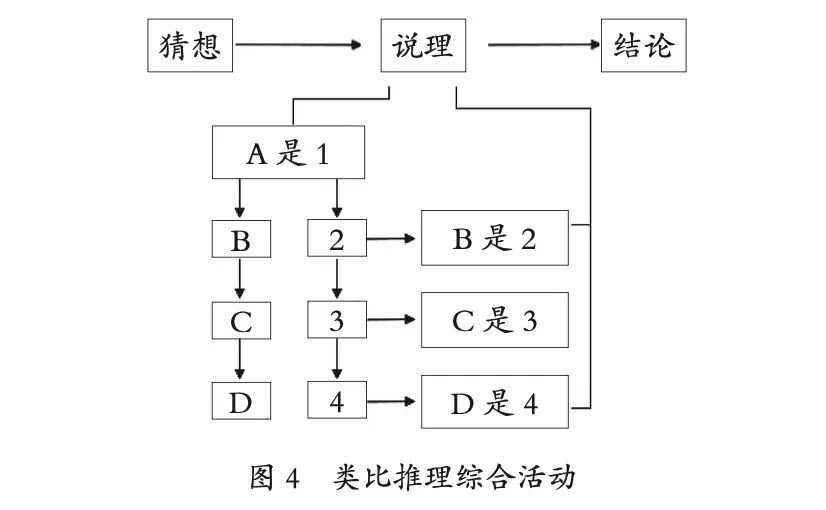
Analogical reasoning comprehensive activities mainly include three modules: conjecturing, reasoning, and concluding. Among them, reasoning is the central link, mainly conducted through analogical explanations. As shown in Figure 4, based on the conclusion that A is 1, find a similar B, and find a similar 1, which is 2, leading to the conclusion that B is 2; similarly, further find a similar C and 2, which is 3, leading to the conclusion that C is 3, and thus forming a conclusion based on the analogical results.

For example, in the lesson on “sum of interior angles of polygons,” the process of analogical reasoning comprehensive activity is shown in Figure 5. Step 1: Trigger conjecture. Based on existing materials, trigger the conjecture regarding the sum of the interior angles of polygons. Step 2: Reasoning induction. Based on the interior angle sum of triangles being 180°, quadrilaterals being 360°, and pentagons being 540°, combine graphical segmentation to inductively summarize the pattern. Step 3: Confirm conclusion.

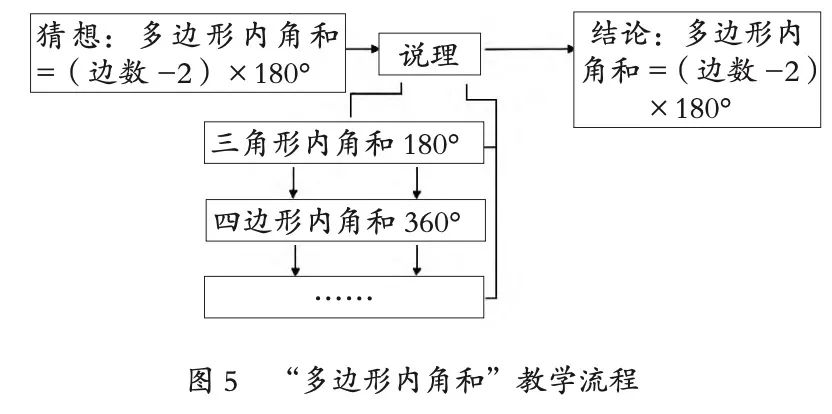
3. Deductive Reasoning Comprehensive Activity Module Combination

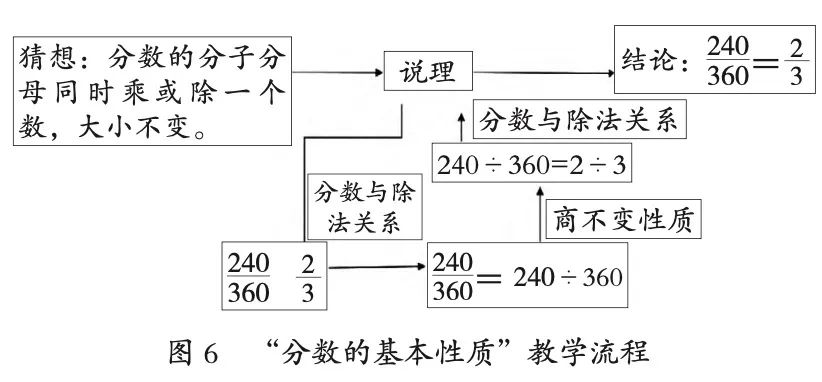
Deductive reasoning comprehensive activities mainly include three modules: conjecturing, reasoning, and concluding. Among them, reasoning is the central link, mainly deriving new conclusions based on known information and existing mathematical facts (properties, theorems, meanings, etc.). In the reasoning process, if one reasoning cannot arrive at the final conclusion, continue reasoning based on properties, theorems, and meanings until a final conclusion is formed. For example, in the lesson on “basic properties of fractions,” the process of deductive reasoning comprehensive activity is shown in Figure 6. Step 1: Propose conjecture. First, based on existing information, propose a conjecture. Step 2: Reasoning exemplification. First, relate fractions to division, transforming 360 into 240÷360; then through the property of unchanged quotient, transform 240÷360 into 2÷3; finally, relate fractions to division to draw conclusions. Step 3: Confirm conclusion. Summarize to derive the basic properties of fractions.

Multiple Reasoning Learning Paths Based on Teaching Differences

Based on differences in reasoning types, content structures, and cognitive levels, around the same lesson or reasoning activity, various combinations of conjecturing, reasoning, and exemplifying activity modules can be explored from different angles to promote the integration and progress of reasonable and deductive reasoning.

1. Multiple Styles Based on Differences in Reasoning Types

The same teaching content can be designed with different learning paths based on different reasoning types. Reasonable reasoning can adopt a learning path of “operational observation—forming conjectures—exemplification reasoning—confirming conclusions”. For example, in the lesson on “basic properties of fractions,” the learning path for reasonable reasoning is: (1) Draw it. Present equal fractions, using shading in a square to represent the meaning of fractions. (2) Compare it. Based on the size of the shaded area, discuss what relationships exist among these three fractions. (3) Write it. Can more equal fractions be written? (4) Speak it. What kinds of fractions are equal? Deductive reasoning can adopt a learning path of “connecting associations—forming conjectures—exemplification reasoning—confirming conclusions.” Similarly, in the lesson on “basic properties of fractions,” the learning path for deductive reasoning is: (1) Activate the question. Are there equal fractions? Write it down. (2) Boldly speculate. Guess what kinds of fractions maintain the same size. (3) Exemplification reasoning. These fractions have different units; how to prove they are equal? (4) Confirm conclusions. Discuss the rules just studied. Although both reasonable and deductive reasoning can arrive at the same conclusion, the reasoning processes, methods, and thinking styles perceived by students are different.

2. Multiple Styles Based on Content Structure Differences

Based on differences in the structure of different knowledge content and the structure differences in handling the same content, multiple styles such as single-type, iterative, and extension-type can be constructed. Single-type structures are suitable for content with less interconnection, with the reasoning activity framework being “conjecturing—verifying”; for example, “mental calculations of whole tens and hundreds multiplied by one-digit numbers” falls under this reasoning activity framework. Iterative structures are suitable for more difficult knowledge content, progressing in layers, with the reasoning activity framework being “conjecturing—verifying—conjecturing—verifying…” Iterative reasoning structures apply to relatively complex teaching content, including two categories: one is the iteration of different conjecture forms, such as the reasoning framework for “sum of interior angles of triangles,” which plants the seeds for subsequent “sum of interior angles of polygons”. The other is the iteration of multiple conjecture forms, where students cannot obtain the final mathematical conjecture in one go, such as the “basic properties of proportions,” which can be conjectured by comparing equal fractions, ratios, and divisions, first speculating on their similarities and differences, reasoning through transformations; then conjecturing the basic properties of proportions, and subsequently proving based on interrelationships, iterating continuously. Extension-type reasoning activity frameworks are structured as “conjecturing—verifying—extending conjectures,” which is a typical analogical reasoning, suitable for deriving one conclusion to another similar conclusion, serving as an important form for generating knowledge connections and promoting autonomous learning among students. For example, “commutative law” and “characteristics of multiples of 9” can both adopt this structure for learning.

3. Multiple Styles Based on Cognitive Level Differences

Students’ existing cognitive level differences significantly impact reasoning activities. Based on students’ varying degrees of understanding of reasoning conclusions, multiple learning paths can be formed, such as discovery-based and verification-based. Discovery-based is suitable when most students are unaware of the research conclusions, with a path of “experiment—conjecturing—reasoning—conclusion,” focusing on discovering patterns. Verification-based is suitable when most students already know the conclusions, with a path of “conjecturing—experimenting—reasoning—conclusion,” focusing on verifying patterns. For example, in the lesson on the “volume of rectangular prisms,” suitable learning paths can be selected based on students’ understanding of the volume formula. In the discovery-based learning path, through experimental operations, students observe the relationships between the number of unit cubes arranged and the dimensions of the rectangular prism, using incomplete inductive reasoning to derive the volume formula; in the verification-based learning path, through experimental operations, they verify the known volume formula. Although the learning paths differ, both can promote the development of students’ reasoning awareness.

References

• [1] Ministry of Education of the People’s Republic of China. Compulsory Education Math Curriculum Standards (2022 Edition) [S]. Beijing: Beijing Normal University Press, 2022:9-13.

• [2] Song Yuyang. “Conjecturing,” “Reasoning,” “Exemplifying” Activity Design: Significance, Connotation, and Dimensions [J]. Jiangxi Education, 2020(35):16-20.

• [3] Zhang Dan. The Connotation of Reasoning Ability and Teaching Suggestions [J]. Elementary Teaching: Math Edition, 2018(05):9-12.

• [4] Cao Peiying. Crossing the Gap, Getting Out of Misunderstandings: Interpretation and Practical Research of Core Terms in the “Math Curriculum Standards” [M]. Shanghai Education Press, 2017:123-147.