Recently, a piece of news that originated from foreign media and was widely spread by domestic media has caused a stir in the mathematics community: the Riemann Hypothesis has been proven. Meanwhile, the blockchain community is also buzzing, suggesting that encryption algorithms may be compromised.
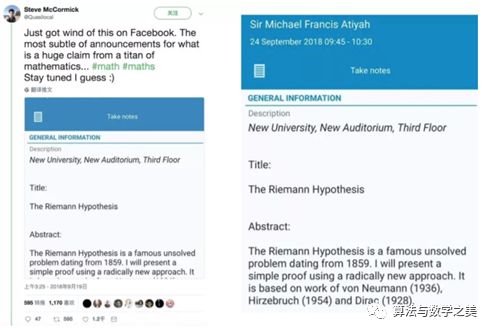
Fields Medal and Abel Prize winner, Sir Michael Atiyah (April 22, 1929 -), former President of the Royal Society, claims to have proven the Riemann Hypothesis and will present at the Heidelberg Laureate Forum on September 24. It is known that Atiyah’s main research area is geometry, and he is regarded as one of the greatest mathematicians of our time.

Michael Atiyah (1924-)
The status of the Riemann Hypothesis in the mathematics community is undeniable. Proposed by mathematician Riemann in 1859, it is considered one of the most important and eagerly awaited problems in contemporary mathematics, having troubled humanity for a century and a half.
What is the Riemann Hypothesis?
Prime numbers are natural numbers greater than 1 that cannot be divided by any other natural numbers except for 1 and themselves, such as 2, 3, 5, etc. Mathematicians have long proven that there are infinitely many prime numbers, but what patterns do these primes follow on the number line, or is there really an exact pattern?
Riemann extended Euler’s function related to prime number distribution, the zeta function, to apply to the entire complex plane. He conjectured that all non-trivial zeros of the extended Riemann zeta function lie on the line where the real part equals 1/2.
Prominent mathematician Lu Changhai summarized it this way (abridged version):
Roughly speaking, it is a conjecture about a complex variable function known as the Riemann zeta (ζ) function (a function where both the variable and the function value can take values in the complex domain). Like many other functions, the Riemann ζ function takes the value of zero at certain points, which are called the zeros of the Riemann ζ function. Among those zeros, some are particularly important and are called the non-trivial zeros of the Riemann ζ function. The Riemann Hypothesis conjectures that all those non-trivial zeros are distributed along a special line known as the “critical line”.
Detailed version:
As early as 1737, the great mathematician Euler discovered the connection between the distribution of prime numbers and the Zeta function, providing and proving the Euler product formula, making the Zeta function a classical method for studying prime number problems.
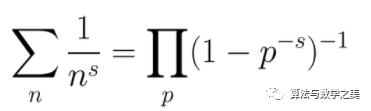
Euler’s product formula, where p is a prime number and n is a natural number
The Riemann Hypothesis (Riemann Hypothesis) was first proposed by great mathematician Riemann in 1859, discussing the non-trivial solution problem of the Riemann Zeta function.
The Riemann Hypothesis is a conjecture about the distribution of zeros of the Riemann Zeta function. The Riemann Zeta function looks like this:
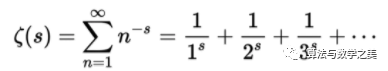
The Riemann Zeta function has two types of zeros: one type is the zeros located on the real number axis, known as trivial zeros, while the other type is the zeros located in other regions of the complex plane, known as non-trivial zeros. Mathematicians have already proven that all these non-trivial zeros lie within the complex plane where the real part ranges from 0 to 1, while Riemann boldly conjectured that all these non-trivial zeros lie on a straight line where the real part is 1/2. This is the Riemann Hypothesis!
For more information about the Riemann Hypothesis, please refer to:
New Developments in Riemann Hypothesis Proof
The Soul of Primes—Riemann and His Great Conjecture
What is the Connection Between Riemann Hypothesis and Goldbach’s Conjecture?
The Seven Great Mathematical Problems of the World and Hilbert’s 23 Problems
As of now, many mathematical propositions in academic papers are based on the assumption that the Riemann Hypothesis (or its generalization) holds. If the Riemann Hypothesis is confirmed or proven, these mathematical propositions will be elevated to the status of theorems; conversely, if it is disproven, it means that over a thousand mathematical propositions will not hold.
Therefore, based on this research significance, the mathematics community is particularly attentive to Michael Atiyah’s presentation on September 24. Besides the research significance, the Riemann Hypothesis can reveal the statistical laws of prime distribution, which has a certain connection with encryption algorithms that rely on prime numbers, triggering some blockchain self-media and cryptocurrency enthusiasts’ excitement.
Research indicates that the distribution of prime numbers has always been difficult to capture, and Riemann pointed out in his paper that the distribution of prime numbers is entirely contained within a special function (the Riemann function), which forms the basis of the Riemann Hypothesis regarding the distribution of primes. Currently, the encryption algorithms used in the blockchain field are somewhat related to the distribution trajectory of primes.
Some believe that if the Riemann Hypothesis is proven, it could potentially impact the logic of encryption algorithms, such as how encryption algorithms and hash functions interact, possibly even compromising encryption algorithms, thus affecting the cryptocurrency sector.
To address this topic, several experts in encryption algorithms and cryptography were interviewed. Based on their views, the general consensus can be summarized as:Even if the Riemann Hypothesis is proven, it has nothing to do with blockchain encryption algorithms.
A representative from a well-known technology media outlet stated, from a theoretical perspective, that “the encryption algorithms that rely on prime numbers” are basically RSA. Although RSA has some applications in general industrial encryption, such as the elliptic curve encryption modified for Bitcoin, other cryptocurrencies rarely use RSA, so it is not closely related to the Riemann Hypothesis.
From an application perspective, “the proposition of the Riemann Hypothesis is complete; as long as it is considered true, it can be used without waiting for it to be ‘proven true’. Moreover, I have never heard of the Riemann theorem playing an important role in any attack methods for any field.”
Another engineer working on consensus algorithms for public chains stated that for most blockchain technologies, the hash algorithms used are unrelated to primes, and the asymmetric algorithm used is ECC, which is based on the discrete logarithm problem over elliptic curves and also unrelated to primes.
“To take a step back, if one must say there is a connection, it might only be with a project that does ‘prime currency’. This project modifies Bitcoin’s mining algorithm to search for primes, with no other special aspects. Hence, some in the cryptocurrency community are speculating,” this individual remarked, “the Riemann Hypothesis may impact prime prediction, but before the Riemann Hypothesis is proven, everyone agrees on the content of this conjecture, so it can still be used to search for primes.”
Overall, the opinions of these two individuals align. The proving of the Riemann Hypothesis would contribute more to the field of mathematics. In engineering terms, unless the Riemann Hypothesis is disproven, the impact will not be significant!
So, what is the real impact of the Riemann Hypothesis?
Of course, the Riemann Hypothesis is indeed very profound; it has a history of over a century and a half since its inception. During this time, many renowned mathematicians have made strenuous efforts to solve it, yet no one has succeeded. However, if we measure merely by depth, then several other famous mathematical conjectures are equally formidable. For instance, Fermat’s conjecture took over three and a half centuries to be proven; Goldbach’s conjecture was proposed over a century earlier than the Riemann Hypothesis, yet like the Riemann Hypothesis, it remains unproven to this day. These records undoubtedly represent significant challenges!
So, what makes the Riemann Hypothesis the most important mathematical conjecture?
The primary reason is its intricate connections with other mathematical propositions.Statistics show that there are already over a thousand mathematical propositions in today’s mathematical literature that are based on the validity of the Riemann Hypothesis (or its generalizations). This indicates that once the Riemann Hypothesis and its generalizations are proven, the impact on mathematics will be tremendous; all those over a thousand mathematical propositions could be elevated to the status of theorems; conversely, if the Riemann Hypothesis is disproven, then almost inevitably, some of those over a thousand mathematical propositions will also become invalid.
Secondly, the Riemann Hypothesis is closely related to the distribution of primes in number theory. Number theory is a very important traditional branch of mathematics, referred to by the German mathematician Gauss as the “queen of mathematics.” The distribution of primes is a crucial traditional topic in number theory, which has always attracted the interest of numerous mathematicians. This deep-rooted “noble lineage” also increases the Riemann Hypothesis’s status and importance among mathematicians.
Furthermore, an important criterion for the significance of a mathematical conjecture is whether it can generate results that contribute to other areas of mathematics during the study of the conjecture.Using this standard, the Riemann Hypothesis is also extremely important. In fact, one of the early results achieved by mathematicians in studying the Riemann Hypothesis directly led to the proof of an important proposition regarding the distribution of primes—the Prime Theorem—which itself was also an important conjecture with over a hundred years of history before being proven.
Lastly, and perhaps most surprisingly, isthe importance of the Riemann Hypothesis even extends beyond pure mathematics and “intrudes” into the realm of physics. In the early 1970s, it was discovered that certain studies related to the Riemann Hypothesis had significant correlations with some very complex physical phenomena. The reasons for this correlation remain a mystery even today. However, its very existence undoubtedly further enhances the importance of the Riemann Hypothesis.
With so many reasons, the Riemann Hypothesis is rightly called the most important mathematical conjecture.
∑ Edited by | Gemini
Source | Compiled from the internet

Algorithm Mathematics Beauty WeChat public account welcomes contributions
The articles involve mathematics, physics, algorithms, computer science, programming, and related fields. Upon acceptance, we will offer remuneration.
Submission email: [email protected]