Click the above“blue text” to follow us!

Ordinary differential equations are relationships composed of independent variables, unknown functions, and derivatives (or differentials) of functions, closely related to physics, astronomy, and the rapidly evolving fields of science and technology. Newton used differential equations as a tool while studying celestial mechanics and classical mechanics, theoretically deriving the laws of planetary motion.
In reflecting the relationships between quantities in the motion processes of the objective reality world, there exist numerous mathematical models that satisfy the relationships of ordinary differential equations, such as population growth, infectious disease spread, and chemical workshop ventilation, all reflecting the important role of ordinary differential equations in mathematical modeling. Therefore, learning the basic statements of Matlab for solving ordinary differential equations is essential for establishing and solving our mathematical models. This article mainly introduces two forms of function solving: symbolic solving and numerical solving.
1.MatlabSymbolicSolving FunctionThe function used isdsolve
Specific format:
(1)a=dsolve(‘ordinary differentialequation’)
The output result is the solution of the ordinary differential equation;
(2)a=dsolve(‘equation’,‘condition1’,‘condition2’,…,‘x’)
Used to solve ordinary differential equations that satisfy several initial conditions, where the independent variable isx;
(3)A=dsolve(‘equation1’,‘equation2’,…,‘condition1’,‘condition2’,…)Used to solve multiple differential equations and output the results in a structured format.
Things to note when calling the function:
InMatlab, D represents differentiation of the variable in the differential equation, D2, D3 represent the second and third derivatives, respectively, and so on.
Example:D3z means taking the third derivative of the variable z.
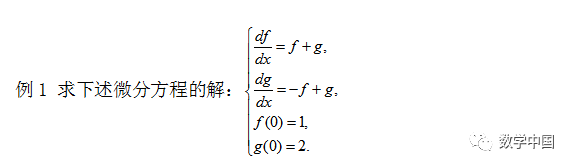
Solution:
The Matlab command is:

2.Matlab Numerical Solving Function
General format:[x,y]=solver(filename,xspan,y0,[option])
Where,x and y are the node vectors and corresponding numerical solutions;filename is the function name of the differential equation, which must return a column vector;
xspan is the solving interval, specifically in the form of [x0,xf];
y0 is the given initial value;
option is an optional parameter to change solving characteristics;
solver is the function for obtaining numerical solutions of ordinary differential equations, with various forms, and the table below lists some commonly used functions and their corresponding numerical methods, which can be selected as needed.
|
Solving Function |
Numerical Method Used |
|
ode23 |
2-3 order Runge-Kutta method |
|
ode45 |
4-5 order Runge-Kutta method |
|
ode113 |
Adams method, accuracy can reach up to |
|
ode23t |
Trapezoidal method |
|
ode15s |
Backward numerical differentiation method, medium accuracy |
|
ode23s |
2nd order Rosebrock method, low accuracy |
|
ode23tb |
Trapezoidal method, low accuracy |
Example 2: Solve the following initial value problem numerically
The exact solution is
Solution:
1.Create function filefun1.m
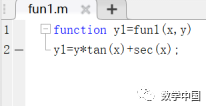
2.Solve the differential equation, the Matlab command is:

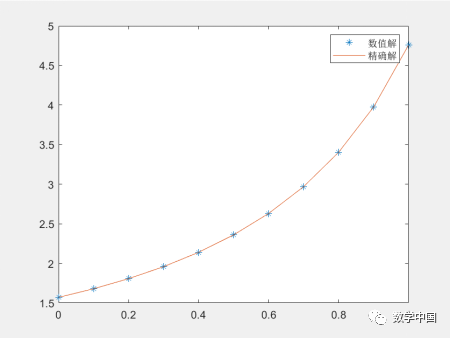
3.Plot to compare the numerical solution and the exact solution
END
Editor / Liu Guanting
Review / Wang Man Zhen
Recheck / Sun Tianming
Click below
Follow us
