Click the blue text to follow us
Today, we bring you an advanced practical assignment from Liu Ke, a student from the Telecommunications Class 21101 at the School of Mathematics: Matlab Matrix Indexing Methods and Examples.

💭Project Name: Matlab Matrix Indexing Methods and Examples
💭Course Name: Digital Image Processing
💭Completer: Liu Ke, Telecommunications Class 21101
💭Instructor: Li Xiaoqin
Introduction
When exploring the profound world of digital image processing, we must mention its foundation: matrix indexing. Digital image processing, as one of the key technologies in modern computer vision and information processing, encompasses the entire process from image acquisition to image analysis and deeply utilizes the concept of matrix indexing during image processing.
Imagine that a digital image is actually composed of countless tiny pixel points. Each pixel carries a part of the image’s information, which could be color, brightness, or contrast. In computers, these pixel points are organized into a two-dimensional matrix structure, where the position of each pixel corresponds to a specific index in the matrix. The introduction of this matrix structure allows us to process and analyze images in a more mathematical and systematic way. Through matrix indexing, we can accurately locate any pixel point in the image and perform operations on it. Simply put, if the matrix is a cinema, then the matrix index is the seat number, allowing each viewer to find their seat. Similarly, through matrix indexing, we can find the position of each element. Whether it is simple grayscale adjustment, noise elimination, or complex feature extraction and object detection, it relies on the precise positioning and processing of pixel points.
Therefore, it can be said that the core of element positioning and processing in digital image processing is matrix indexing. Matrix indexing not only provides us with an efficient and accurate operational tool but also allows us to understand and process digital images from a deeper and more comprehensive perspective. Next, let’s look at two examples.
One-Dimensional Vector Indexing
Let’s look at an example of one-dimensional vector indexing. The code is as follows:
vector = [2, 5, 6, 8, 9];
element_3 = vector(3);
vector(1) = 10;
last_element = vector(end);
sub_vector = vector(2:3);
A=vector(1 :2 :end);
B=[1 4 5];
C=vector(B);
Can you tell the output of the above commands?
Let’s run it and see the result.
Matlab Code
% Output results
disp('Modified vector elements:');
disp(vector);
disp('Third element:');
disp(element_3);
disp('Last element:');
disp(last_element);
disp('Second and third elements:');
disp(sub_vector);
disp('Every other element');
disp(A);
disp('One vector as the index of another vector');
disp(C);Running Results

Did you get it right?
Next, let’s understand the explanation of each line of code through the following annotated image.

Two-Dimensional Matrix Indexing
Similarly, let’s look at an example of two-dimensional matrix indexing. The code is as follows:
A = [1 2 3 4;5 6 7 8;9 10 11 12];
element = A(2, 3);
row = A(2, :);
col = A(:, 3);
rows = A([1, 3], [2 2]);
B=A(2:end,end:-2:1);
E=logical([1 0 0 0;0 0 0 1;0 0 0 1]);
L=A(E);
Can you tell the output of the above commands?
Let’s run it and see the result.
Matlab Code
% Output results
disp('Two-dimensional matrix:');
disp(A);
disp('Specific element:');
disp(element);
disp('Row 2:');
disp(row);
disp('Column 3:');
disp(col);
disp('Vector as matrix index');
disp(rows);
disp('Non-continuous indexed elements');
disp(B);
disp('Logical index');
disp(L);Running Results

Did you get it right?
Next, let’s understand the explanation of each line of code through the following annotated image.

We have demonstrated the basic usage of Matlab matrix indexing and its ability to solve practical problems through two simple Matlab program examples. If you do not understand these Matlab matrix indexing methods and results, this article provides a detailed explanation of these two examples.
One-Dimensional Vector Indexing Methods
① Direct Indexing: Creating an array with dimensions 1xN (1 row and N columns) is called a row vector. The elements of the row vector are enclosed in square brackets and separated by spaces or commas, for example
>>A=[2 4 6 8 10];
A =
2 4 6 8 10
Using the transpose symbol (.’) can convert a row vector into a column vector. For example: B equals the transpose of A, and B becomes a column vector.
>>B=A.’
B =
2
4
6
8
10
② Single Element Indexing: Directly use the index value (integer) to access or modify a single element in the vector.
A = [2 4 6 8 10]; % Create a one-dimensional vector
element = A(3); % Access the 3rd element, which is 6
A(3) = 10; % Modify the 3rd element to 10
③ End Keyword: In a one-dimensional vector, end also represents the last element of the vector.
A = [2 4 6 8 10];
last_element = A(end); % Access the last element of the vector, which is 10
④ Vector Indexing: Use the colon operator (:) to create a sub-vector.
A = [2 4 6 8 10];
sub_vector = A(2:4); % Select the 2nd to the 4th elements, which are [4 6 8]
The colon can sometimes be used to index all elements in the vector, for example A(:) indexes all elements of vector A and generates a column vector.
>>A(:)
ans =
2
4
6
8
10
Similarly, A(1:end) generates a row vector consisting of all elements.
The above is Matlab’s indexing for a segment of continuous elements. Matlab’s indexing for data is not limited to continuous elements; it also supports non-continuous element indexing, which involves indexing steps. For example, A(1:2:end) means starting from the first element, with a step size of 2, until the last element stops.
>>A(1 :2 :end)
ans=
2 6 10
Of course, the step size can also be negative. For example, A(end:-2:1) means indexing from the last element, with a step size of -2, until the first element stops.
>>A(end:-2:1)
ans=
10 6 2
Additionally, one vector can also be used as an index for another vector. For example, define a vector B=[1 4 5]. Using the defined vector B as an index for A is equivalent to retrieving the 1st, 4th, and 5th elements from vector A.
>>B=[1 4 5]
>>A(B)
ans=
2 8 10
Two-Dimensional Matrix Indexing Methods
Before introducing two-dimensional matrix indexing methods, let’s first understand the meaning of a two-dimensional matrix:
In the Matlab environment, a matrix can be conveniently represented by a column enclosed in square brackets and separated by semicolons.
>>A=[1 2 3 4;5 6 7 8;9 10 11 12]
A=
1 2 3 4
5 6 7 8
9 10 11 12
Directly listing matrix elements is a basic method of defining matrices. Next, we introduce six common matrix generation functions that can be particularly convenient for matrix initialization.
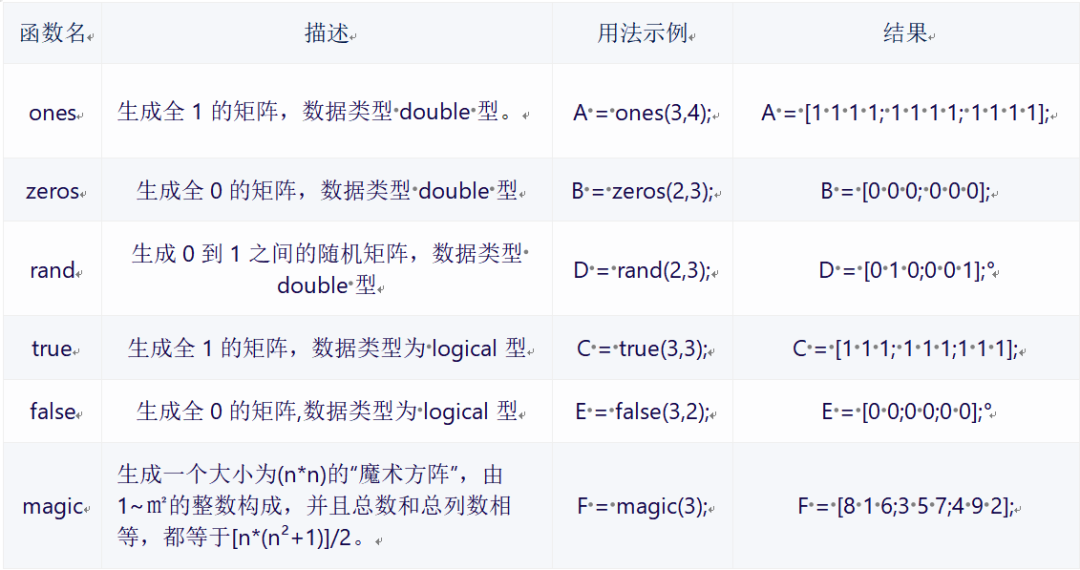
Now, let’s formally introduce two-dimensional matrix indexing methods. Similar to one-dimensional vectors, two-dimensional matrices require two indexes: one to determine the row position of the element and another to determine the column position of the element.
① Single Element Indexing: Use two index values (integers), where the first represents the row and the second represents the column, to access or modify a single element in the matrix.
For example, the command A(3,4) defines the element in the 3rd row and 4th column of the matrix.
>>A(3,4)
ans=
12
② Vector Indexing: Use the colon operator (:) to select an entire row or an entire column in the matrix. You can also use two colon operators to select a block of elements in the matrix (i.e., a rectangular area). For example:
>>A(1,:)
ans=
1 2 3 4
Similarly, A(:,1) extracts the first column elements of all rows.
>>B=A(1:2,:) % This means to extract only the first and second row elements.
B=
1 2 3 4
5 6 7 8
Similarly, B=A(:,1:2) means extracting the first and second column elements of matrix A and copying them to matrix B.
③ End Keyword: When unsure about the specific row or column in the matrix, use end to represent the last row or last column of the matrix. For example:
>>A(end,end) % This means to pick the last row and last column element of matrix A.
12
④ Negative Indexing: Matlab does not support negative indexing to directly access matrix elements. However, you can calculate the positive index to access matrix elements. For example, to access the second-to-last row, you can use end-1 to complete it.
>>A(end-1,end-1)
ans=
7
Similarly, A(2:end,end:-2:1) extracts a block of data consisting of non-continuous elements, indicating starting from the last column with a step size of 2 until stopping at the first column, producing a 2×2 matrix.
>>A(2:end,end:-2:1)
ans=
8 6
12 10
⑤ Logical Indexing: Use a logical array to select elements in the matrix. The size of the logical array must match the original matrix. You can define a logical array using the logical function. The logical array serves as the matrix index, meaning the positions where the logical array is 1 are the index positions, retrieving the elements at those positions in the logical array.
For example:
>>E=logical([1 0 0 0;0 0 0 1;0 0 0 1])
E=
1 0 0 0
0 0 1 0
0 0 0 1
>>A(E)
ans=
1
7
12
⑥ Vector as Matrix Indexing: Use a vector as an index for the matrix to access multiple elements in the matrix. For example, B=A([1 3],[2 4]) means extracting the elements from the first row second column, first row fourth column, third row second column, and third row fourth column of the matrix.
>>B=A([1 3],[2 4])
B=
2 4
10 12
Notes
When using matrix indexing, it is important to pay attention to the legality and validity of the indexes. Indexes that exceed the matrix range will lead to errors or abnormal results. Therefore, when writing code, ensure the correctness of the indexes.
In summary, Matlab’s matrix indexing methods are a powerful and flexible tool that makes matrix operations simple and efficient. By mastering matrix indexing methods, you can perform data processing and analysis tasks more efficiently. By skillfully mastering these indexing techniques, we can more effectively utilize Matlab for data processing and analysis in the future.
Edited by | Li Ting

Scan to Follow Us
We will regularly push content on basic knowledge of digital image processing, introductory image processing algorithms, and implementation of image processing cases.