What is a confusion matrix?
It is a table used to evaluate the model’s error locations in classification problems.
The rows represent the actual categories that the results should belong to, while the columns represent the predictions we made. Using this table, we can easily identify which predictions are incorrect.
Creating a Confusion Matrix
A confusion matrix can be created using predictions from logistic regression.
Now, we will use NumPy to generate the actual values and predicted values:
import numpyNext, we need to generate numbers for the “actual” values and “predicted” values.
actual = numpy.random.binomial(1, 0.9, size = 1000)
predicted = numpy.random.binomial(1, 0.9, size = 1000)To create the confusion matrix, we need to import metrics from the sklearn module.
from sklearn import metricsOnce we import metrics, we can use the confusion matrix function on the actual and predicted values.
confusion_matrix = metrics.confusion_matrix(actual, predicted)To create a more interpretable visual display, we need to convert the table into a confusion matrix display.
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])Visual display requires us to import pyplot from matplotlib.
import matplotlib.pyplot as pltFinally, to display the chart, we can use the plot() and show() functions from pyplot.
cm_display.plot()
plt.show()Example:
import sys
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import numpy
from sklearn import metrics
actual = numpy.random.binomial(1,.9,size = 1000)
predicted = numpy.random.binomial(1,.9,size = 1000)
confusion_matrix = metrics.confusion_matrix(actual, predicted)
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])
cm_display.plot()
plt.show()Result: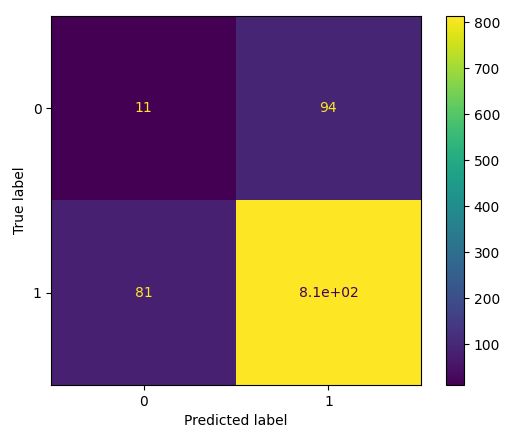
Result Explanation
The created confusion matrix contains four different quadrants:
-
True Negatives (Top Left Quadrant)
-
False Positives (Top Right Quadrant)
-
False Negatives (Bottom Left Quadrant)
-
True Positives (Bottom Right Quadrant)
“True” indicates accurate predictions, while “False” indicates errors or incorrect predictions.
After creating the confusion matrix, we can calculate various metrics to quantify the model’s quality. First, let’s look at accuracy.
Creating Metrics
The matrix provides many useful metrics to help us evaluate the classification model.
Different metrics include: accuracy, precision, sensitivity (recall), specificity, and F1 score, as described below.
Accuracy
Accuracy measures the frequency of correct predictions by the model.
How to calculate
(True Positives + True Negatives) / Total Predictions
Accuracy = metrics.accuracy_score(actual, predicted)Precision
What proportion of the predicted positive cases are actually true positive cases?
How to calculate
True Positives / (True Positives + False Positives)
Accuracy does not assess the correct predictions of negative cases:
Precision = metrics.precision_score(actual, predicted)Sensitivity (Recall)
What proportion of all positive cases are predicted as positive?
Sensitivity (sometimes referred to as recall) measures the accuracy of the model’s positive predictions.
This means it considers true positives and false negatives (i.e., positives incorrectly predicted as negatives).
How to calculate
True Positives / (True Positives + False Negatives)
Sensitivity provides a good understanding of the accuracy of the model predicting something as positive:
Sensitivity_recall = metrics.recall_score(actual, predicted)Specificity
How well does the model predict negative results?
Specificity is similar to sensitivity but measures from the perspective of negative results.
How to calculate
True Negatives / (True Negatives + False Positives)
Since it is exactly the opposite of recall, we use the recall_score function with the opposite position label:
Specificity = metrics.recall_score(actual, predicted, pos_label=0)F1 Score
The F1 score is the “harmonic mean” of precision and sensitivity.
It considers both false positives and false negatives, making it suitable for imbalanced datasets.
How to calculate
2 * ((Precision * Sensitivity) / (Precision + Sensitivity))
This score does not consider true negative values:
F1_score = metrics.f1_score(actual, predicted)Example:
import numpy
from sklearn import metrics
actual = numpy.random.binomial(1,.9,size = 1000)
predicted = numpy.random.binomial(1,.9,size = 1000)
Accuracy = metrics.accuracy_score(actual, predicted)
Precision = metrics.precision_score(actual, predicted)
Sensitivity_recall = metrics.recall_score(actual, predicted)
Specificity = metrics.recall_score(actual, predicted, pos_label=0)
F1_score = metrics.f1_score(actual, predicted)
#metrics:print({"Accuracy":Accuracy,"Precision":Precision,"Sensitivity_recall":Sensitivity_recall,"Specificity":Specificity,"F1_score":F1_score})Result:{‘Accuracy’: 0.8, ‘Precision’: 0.8863892013498312, ‘Sensitivity_recall’: 0.8883878241262683, ‘Specificity’: 0.10619469026548672, ‘F1_score’: 0.8873873873873874}