ClickBlue TextFollow Us
Abstract:
The symmetric and asymmetric cryptographic systems each have their own advantages and disadvantages.Exploring a hybrid cryptographic system that combines both, retaining their advantages while maximizing the elimination of their disadvantages, is of great significance for the efficiency and security of modern network communication.Using asymmetric encryption to protect symmetric key is a feasible solution.Under this scheme, attackers cannot bypass the decryption of the asymmetric key to directly attack the ciphertext of the symmetric encryption.The proposal and demonstration of this scheme indicate that various cryptographic systems can be used in combination to complement each other and reinforce their strengths.
The data encryption algorithm was developed by IBM in the early 1970s as a block cipher. Due to its mathematically provable security strength (characterized by diffusion and confusion), and ease of hardware implementation, it has gradually moved from theory to practical application and is widely used in the communication and financial industries. In 1977, it became the officially recognized data encryption standard (Data Encryption Standard, DES) by the U.S. government. However, the DES algorithm still does not solve all the common defects of symmetric encryption algorithms: the distribution of symmetric keys requires additional secure channels. At the same time, with the increase in computer processing speeds, the resistance of the DES algorithm to brute-force attacks has gradually weakened. By the 1990s, when there was explosive growth in internet encrypted traffic, the mainstream data encryption algorithm in network communication was the asymmetric encryption system represented by RSA. This asymmetric encryption algorithm features easy key distribution (not occupying additional channels) and strong resistance to brute-force attacks. The widespread application of asymmetric encryption systems is an inevitable result of technological advancement and the increasing demand for information security.
Today, symmetric encryption algorithms are still applied in many fields such as communication and economics, and have not been eliminated due to technological advancements. The reason for this is that symmetric and asymmetric encryption are not two opposing and mutually exclusive cryptographic systems; they each have their own advantages and disadvantages. Clearly recognizing their complementarity is key to constructing a relatively complete cryptographic system. Although the public key cryptographic system has the advantages of easy key distribution and difficulty in being attacked by brute force, these advantages come at the cost of efficiency. Compared to symmetric algorithms, asymmetric algorithms require more time during encryption and decryption. This makes asymmetric algorithms unsuitable in some scenarios that require immediate response, such as edge computing. This indicates that to achieve higher security strength while not significantly reducing algorithm efficiency, it is essential to organically combine the two cryptographic systems.
This paper selects the symmetric encryption algorithm DES, which has milestone significance in modern cryptography, as the research object, and introduces the idea of asymmetric cryptography to improve it. The proposed improved algorithm retains the original advantages of the DES algorithm while also possessing all the advantages of asymmetric algorithms, making it a cryptographic algorithm adapted for data security protection in modern network communication.
01
DES Algorithm
DES is a block cipher where plaintext is grouped into 64 bits, and the key is also 64 bits. After removing 8 bits for parity, the actual key is 56 bits, resulting in 256 possible key combinations. During encryption, the same key is used to encrypt each group of plaintext sequentially, yielding ciphertext of the same length as the plaintext. Since the key and algorithm remain unchanged during the encryption of each equal-length plaintext group, DES is particularly suitable for implementation in embedded hardware [5]. Before encryption, the plaintext is mapped to initial ciphertext using a permutation function IP. The DES encryption algorithm consists of 16 rounds of iterative encryption, with each round using a key derived from the original key through left rotation, known as a subkey K [6]. Before each iteration, the ciphertext obtained from the previous iteration (if it is the first iteration, the object of encryption is the initial ciphertext) is divided into a left half L (bits 1-32) and a right half R (bits 33-64). R is encrypted with the current subkey using the encryption function f.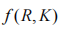
, and after performing an XOR operation with L, the next iteration’s right half R’ is obtained. The next iteration’s left half L’ is assigned from R, which is identical to R. After completing 16 rounds of iteration, the resulting ciphertext is mapped to the final ciphertext using a permutation function.
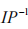The decryption algorithm is the same as the encryption algorithm, using the same key, but the order of the subkeys used in each round of iteration is reversed compared to encryption.
The DES algorithm, after 16 rounds of iteration, has been proven to have sufficient resistance against statistical and linear analysis attacks. Thus, the only way to crack the ciphertext of 16 rounds of DES is through brute force, i.e., trying all 256 possible keys through exhaustive search, which was considered an impossible task when the DES algorithm was first proposed. However, with the increase in computer processing speeds and the maturity of parallel computing technology, the security of DES has been significantly weakened.
02
Improvement of DES Algorithm
The principle of improving the DES algorithm is to use RSA to protect the DES key while adding shuffling and interference processing to the plaintext before encryption.
2.1 Overall Design of the Improvement Scheme
The DES algorithm’s key is a symmetric key and must be transmitted through a secure channel. To allow it to be transmitted over public channels such as the internet, it must be protected using a public key cryptographic system. The most commonly used public key algorithm is RSA; therefore, we can “package” the DES key in an RSA-encrypted “header” and then attach this header to the front of the DES ciphertext, forming a ciphertext package (Encrypted Data Packet), which is then sent to the recipient. “Packaging” mainly refers to encrypting the DES key with the recipient’s public key. Upon receiving the ciphertext package, the recipient first decrypts the header with their private key, retrieves the DES key, and then uses it to decrypt the data portion of the ciphertext package (i.e., the DES ciphertext) to obtain the plaintext.
If the information in the header only contains the DES key, it does not significantly enhance attack resistance; it merely resolves the issue of distributing keys over public channels. Attackers can still use brute force against the data portion of the ciphertext package. To increase the difficulty of brute-force attacks, the header of the ciphertext package must include some information that helps raise the difficulty of brute-force cracking without significantly affecting the RSA decryption efficiency of the header. The two main strategies that can be adopted are: (1) Pre-shuffling the plaintext to confuse the original order; (2) Inserting invalid information before DES encryption, such that attackers must remove this invalid information to obtain valid ciphertext groups and attempt brute-force cracking on these groups.
2.2 Detailed Description of the Improved Algorithm
The improved algorithm includes the structure of the ciphertext package, preprocessing of the plaintext, and the encryption process, as well as the structure of the header of the ciphertext package.
2.2.1 Overall Structure of the Ciphertext Package
The ciphertext package consists of a header and ciphertext. Since the header is RSA-encrypted ciphertext, this paper refers to it as the “RSA header.” The plaintext is encrypted using the key set in the RSA header to generate the ciphertext portion. Due to the insertion of invalid information, the lengths of the ciphertext and plaintext portions are not equal, greatly increasing the difficulty of cracking. The “key set” not only includes the DES key but also contains keys used at various stages of the encryption or decryption process, of which DES encryption or decryption is just one stage. To facilitate the recipient in separating the header, the length of the RSA header is fixed and can only be decrypted using the recipient’s private key.
2.2.2 Preprocessing of the Original Plaintext
Before encryption, the original plaintext P needs to be preprocessed, and the detailed process is described below.
(1) Grouping. The grouping length is consistent with that of DES encryption (64 bits), and the last group is padded with 0s if it is less than 64 bits.
(2) Segmentation. A segment is a higher-level unit than a group, containing 64 groups, and the last segment is padded with 0s if it is less than 64 groups.
The preprocessed plaintext is denoted as P0, yielding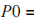
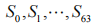, where
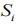is the i-th segment of P0,
(
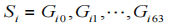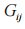is the j-th group of the segment),
(
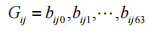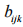is the k-th bit in the group).
The entire encryption process requires three rounds of encryption, denoted as U, J, D, and each ciphertext after encryption is denoted as A, B, C, respectively. Figure 1 illustrates the input/output relationship between the three rounds of encryption.
Figure 1 Encryption Process
2.2.3 Structure of the Ciphertext Package Header
The RSA header includes three key fields and some auxiliary fields (as shown in Figure 2). The key fields store three keys corresponding to the three stages of the encryption process U, J, C. The auxiliary fields mainly store control and verification information. The names, lengths, and purposes of these fields are described below.
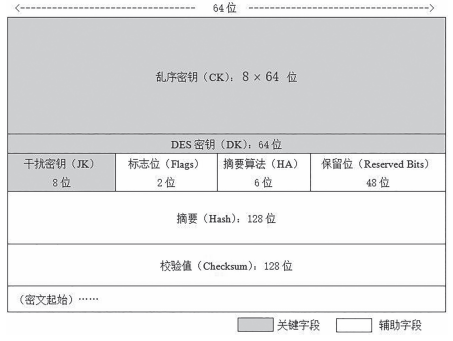
Figure 2 Layout Structure of RSA Header
(1) Confusing Key (CK). The role of the confusing key is to rearrange each segment of plaintext (Reshuffle). Its length is 64 bytes, with the highest bit always being 0, the lowest bit being the parity bit, and the middle 6 bits converted to a decimal number representing an encryption parameter,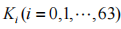
where i is the byte index. The shuffling encryption algorithm is
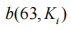, indicating that the i-th group of ciphertext is formed by the bits of the j-th group of plaintext.
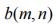is the n-th bit of the m-th group, satisfying
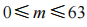(2) Jamming Key (JK). The role of the jamming key is to insert invalid information into each group of ciphertext A to increase the difficulty of cracking. Its length is 8 bits, with the first 6 bits indicating the position of the inserted value in the group
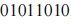, and the last two bits are the value to be inserted. For example, if the jamming key is
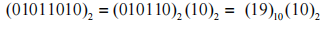, it can be seen that the decimal value of the first 6 bits of the jamming key is 19, hence J=19, and the binary 10 will be inserted in front of the 19th bit of the target group. The jamming key is only applied to the first group of ciphertext A; thereafter, it will change dynamically. The jamming key applied to the second group of ciphertext A will be generated from the first group of plaintext. The method involves placing an 8-bit empty byte (window) at the starting position of the first group of plaintext (i.e., bit 0), where the highest bit of the window corresponds to bit 0 of the group, and the byte displayed in the window will be the jamming key for the second group. Similarly, the window will be placed at bit 1 of the second group to obtain the jamming key for the third group. By shifting the window right one bit each time, the jamming key for the next group can be obtained. If the window crosses the right boundary of the group, the bits that cross will cycle back to the beginning of the group. This method of insertion has a flaw; the length of the ciphertext group is fixed at 66 bits (due to the fixed 2-bit insertion), making it easy for attackers to separate valid groups from the ciphertext and then crack the valid groups. To make the length of the inserted groups variable, the length of the insertion will be changed, specifically starting from the second group, causing the last two bits of the jamming key to change from “content of insertion” to “length of insertion.” The content of the insertion will be taken from the window, and the length of the segment to be inserted will be indicated by the last two bits. Similarly, when taking the insertion, the background group will be treated as a circular connection.
(3) DES Key (DK). The DES key has the same role, form, application method, and classic DES encryption key as before, occupying 64 bits in the RSA header, and it acts on the result of the jamming encryption B to produce ciphertext C.
(4) Flags. The flags occupy 2 bits, indicating whether jamming encryption and shuffling encryption were used during the encryption process.
(5) Hash Algorithm (HA). The hash algorithm occupies 6 bits and is applied to a specific part of the RSA header to yield the value of the hash field. The specific part refers to the part of the RSA header from the start to the flag bit (including the flag bit), referred to as the “upper segment” in this paper. This field can represent up to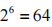
hash algorithms, including commonly used MD5 Message-Digest Algorithm (MD5), Secure Hash Algorithm (SHA), and others.
(6) Reserved Bits. Unused bits reserved for optimization of the algorithm.
(7) Hash. The hash is the hash value obtained by applying the “hash algorithm” specified in the RSA header to the upper segment, with a length of 128 bits.
(8) Checksum. The checksum is the verification value of the ciphertext portion, using the hash algorithm specified by the “hash algorithm” field, with a length of 128 bits.
2.2.4 Encryption and Decryption Process
The encryption process is described as follows.
(1) Preprocess the original plaintext P to obtain P0.
(2) Randomly generate three keys, CK, JK, DK.
(3) Apply CK to P0 to obtain A.
(4) Apply JK to A to obtain B.
(5) Apply DK to B to obtain C.
(6) Fill in the fields of the RSA header.
(7) Calculate and fill in the hash and checksum fields.
(8) Encrypt the plaintext of the RSA header using the recipient’s public key to obtain the header of the ciphertext package.
(9) Connect the header of the ciphertext package and ciphertext C to form a complete ciphertext package.
The decryption process is the reverse of the encryption process, and attention should be paid to the following points.
(1) It is easy to separate the header of the ciphertext package since its length is fixed at 896 bits.
(2) When decrypting the header of the ciphertext package, the recipient’s private key must be used.
(3) When applying JK to B (to remove invalid information), it starts from the first group rather than the last group. That is, the first group is restored using JK, and then the jamming key for the second group is obtained by cyclically shifting the 8-bit window to restore the second group, and so forth.
(4) There is no inverse algorithm for preprocessing, so it does not need to be executed during decryption.
03
Analysis of Attack Resistance of the Improved DES Algorithm
The improved DES algorithm proposed in this paper does not rely on a single symmetric key; rather, it is composed of a key set consisting of three independent keys CK, JK, DK, which are protected by RSA encryption. Even if an attacker attempts to brute-force crack the key set CK, JK, DK, the number of possible key combinations they face is: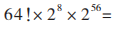
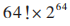, which has sufficient strength to resist brute-force attacks achievable with current computational technology.
Regarding defense against statistical analysis attacks, the diffusion confusion achieved by DES encryption effectively counters statistical attacks. This is one of the advantages of the classic DES algorithm, and the algorithm presented in this paper fully retains this advantage.
For defenses against mathematical analysis methods such as differential and linear analysis, the use of multiple keys inevitably leads to a significant increase in the number of analysis parameters, making mathematical analysis more challenging. Additionally, the staged encryption process makes it difficult to use a single mathematical analysis method to crack this algorithm. This indicates that symmetric and asymmetric cryptographic systems can be used in combination in practice, complementing each other and reinforcing their strengths.
04
Conclusion
This paper proposes an improved algorithm based on the classic DES encryption algorithm. The design concept is to use asymmetric cryptography to protect the DES key, creating a “key shell” that forms a community of defense against cracking along with the ciphertext; simultaneously, it adds shuffling and jamming encryption based on DES encryption, with keys also protected by the key shell, making it impossible for attackers to perform brute-force cracking on the ciphertext without breaking the key shell first. However, the software and hardware implementation methods and performance of this algorithm still require further evaluation and testing, which relates to the range and scenarios in which it can be practically applied.
Editor:Chen Shijiu
Review: Shang Mijun
Call for Papers
Click to Purchase “2020-2021 China Commercial Cryptography Industry Development Report”
Source: Information Security and Communication Confidentiality Magazine
Note: All content is sourced from the internet, and copyright belongs to the author. If there is any infringement, please contact us, and we will handle it as soon as possible.
