For a faster version, see the C language implementation of FFT and IFFT source code, which does not rely on a specific platform.
The porting is very simple, does not rely on other libraries, and allows custom point counts.
The algorithm is based on the usage instructions of the FFT algorithm and the C language implementation source code — Original author: Ji Shuaihu.
Source Code
FFT.c
/*********************************************************************Fast Fourier Transform C program package function introduction: This package is a general Fast Fourier Transform C language function, highly portable, the following parts do not depend on hardware. This package uses a union to represent a complex number, the input is a complex number in natural order (the input real number can set the imaginary part of the complex number to 0), and the output is the complex number in natural order after FFT transformation. This package can call the create_sin_tab() function to create a sine function table during initialization, and later can use the lookup method to calculate the time-consuming sin and cos operations, speeding up the computable speed. Compared to Ver1.1, Ver1.2 only established 1/4 of the sine wave sample values when creating the sine table, saving FFT_N/4 storage space. Usage instructions: To use this function, simply change the macro definition of FFT_N to realize the change in point count. FFT_N should be a power of 2, and if this condition is not met, zeros should be padded at the end. If using the lookup method to calculate sin and cos values, the create_sin_tab() function should be called before calling the FFT function to create the sine table function call: FFT(Compx); Author: Ji Shuaihu Time: 2010-2-20 Version: Ver1.2 References:**********************************************************************/#include <math.h>#include "FFT.h"
struct compx Compx[FFT_N] = {0}; //FFT input and output: stored starting from Compx[0], defined according to size
double SIN_TAB[FFT_N / 4 + 1]; //Define storage space for sine table
/*******************************************************************Function prototype: struct compx EE(struct compx b1,struct compx b2) Function function: Multiply two complex numbers Input parameters: Two complex numbers a,b defined by union Output parameters: The product of a and b, output in union form*******************************************************************/struct compx EE(struct compx a, struct compx b){ struct compx c; c.real = a.real*b.real - a.imag*b.imag; c.imag = a.real*b.imag + a.imag*b.real; return(c);}
/******************************************************************Function prototype: void create_sin_tab(double *sin_t) Function function: Create a sine sampling table, the number of sampling points is the same as the number of points for Fourier transform Input parameters: *sin_t pointer to the array storing the sine table Output parameters: None******************************************************************/void create_sin_tab(double *sin_t){ int i; for (i = 0; i <= FFT_N / 4; i++) sin_t[i] = sin(2 * PI*i / FFT_N);}
/******************************************************************Function prototype: void sin_tab(double pi) Function function: Calculate the sine value of a number using the lookup method Input parameters: pi The radian value to calculate the sine, range 0--2*PI, needs conversion if not satisfied Output parameters: The sine value of the input value pi******************************************************************/double sin_tab(double pi){ int n; double a = 0; n = (int)(pi*FFT_N / 2 / PI);
if (n >= 0 && n <= FFT_N / 4) a = SIN_TAB[n]; else if (n>FFT_N / 4 && n<FFT_N / 2) { n -= FFT_N / 4; a = SIN_TAB[FFT_N / 4 - n]; } else if (n >= FFT_N / 2 && n<3 * FFT_N / 4) { n -= FFT_N / 2; a = -SIN_TAB[n]; } else if (n >= 3 * FFT_N / 4 && n<3 * FFT_N) { n = FFT_N - n; a = -SIN_TAB[n]; }
return a;}
/******************************************************************Function prototype: void cos_tab(double pi) Function function: Calculate the cosine value of a number using the lookup method Input parameters: pi The radian value to calculate the cosine, range 0--2*PI, needs conversion if not satisfied Output parameters: The cosine value of the input value pi******************************************************************/double cos_tab(double pi){ double a, pi2; pi2 = pi + PI / 2; if (pi2>2 * PI) pi2 -= 2 * PI; a = sin_tab(pi2); return a;}
/*****************************************************************Function prototype: void FFT(struct compx *xin) Function function: Perform Fast Fourier Transform (FFT) on the input complex array Input parameters: *xin pointer to the first address of the complex structure array, struct type Output parameters: None*****************************************************************/void FFT(struct compx *xin){ register int f, m, nv2, nm1, i, k, l, j = 0; struct compx u, w, t;
vn2 = FFT_N / 2; //Bit reversal operation, i.e., change natural order to bit-reversed order, using the Radix algorithm nm1 = FFT_N - 1; for (i = 0; i < nm1; ++i) { if (i < j) //If i<j, perform bit reversal { t = xin[j]; xin[j] = xin[i]; xin[i] = t; } k = nv2; //Calculate the next bit-reversed order of j while (k <= j) //If k<=j, indicates the highest bit of j is 1 { j = j - k; //Change the highest bit to 0 k = k / 2; //k/2, compare the next highest bit, and so on, compare one by one until a bit is 0 } j = j + k; //Change 0 to 1 }
{ int le, lei, ip; //FFT operation core, complete FFT operation using butterfly operation f = FFT_N; for (l = 1; (f = f / 2) != 1; ++l); //Calculate the value of l, i.e., calculate the number of butterfly stages for (m = 1; m <= l; m++) // Control the number of butterfly stages { //m indicates the m-th butterfly, l is the total number of butterfly stages l=log(2)N le = 2 << (m - 1); //le butterfly distance, i.e., the distance between the m-th butterfly points lei = le / 2; //The distance between the two points participating in the operation in the same butterfly u.real = 1.0; //u is the butterfly operation coefficient, initial value is 1 u.imag = 0.0; w.real = cos_tab(PI / lei); //w is the coefficient ratio, i.e., the current coefficient divided by the previous coefficient w.imag = -sin_tab(PI / lei); for (j = 0; j <= lei - 1; j++) //Control calculation of different types of butterflies, i.e., calculate butterflies with different coefficients { for (i = j; i <= FFT_N - 1; i = i + le) //Control the same butterfly operation, i.e., calculate butterflies with the same coefficient { ip = i + lei; //i, ip respectively indicate the two nodes participating in the butterfly operation t = EE(xin[ip], u); //Butterfly operation, see formula xin[ip].real = xin[i].real - t.real; xin[ip].imag = xin[i].imag - t.imag; xin[i].real = xin[i].real + t.real; xin[i].imag = xin[i].imag + t.imag; } u = EE(u, w); //Change coefficient for the next butterfly operation } } }}
/*****************************************************************Function prototype: void Get_Result(struct compx *xin, double sample_frequency) Function function: Calculate the modulus of the transformed result, stored in the real part of the complex number, frequency stored in the imaginary part of the complex number, valid data is the first FFT_N/2 numbers Input parameters: *xin pointer to the first address of the complex structure array, struct type, sample_frequency: Sampling frequency Output parameters: None*****************************************************************/void Get_Result(struct compx *xin, double sample_frequency){ int i = 0; for (i = 0; i < FFT_N / 2; ++i) { //Calculate the modulus of the transformed result, stored in the real part of the complex number xin[i].real = sqrt(xin[i].real*xin[i].real + xin[i].imag*xin[i].imag) / (FFT_N >> (i != 0)); xin[i].imag = i * sample_frequency / FFT_N; }}
/*****************************************************************Function prototype: void Refresh_Data(struct compx *xin, double wave_data) Function function: Update data Input parameters: *xin pointer to the first address of the complex structure array, struct type, id: label, wave_data: value of a point Output parameters: None*****************************************************************/void Refresh_Data(struct compx *xin, int id, double wave_data){ xin[id].real = wave_data; xin[id].imag = 0;}FFT.h
#ifndef FFT_H
#define FFT_H
#define FFT_N 16 //Define the number of points for Fourier transform
#define PI 3.14159265358979323846264338327950288419717 //Define the value of pi
struct compx { double real, imag; }; //Define a complex number structure
extern struct compx Compx[]; //FFT input and output: stored starting from Compx[0], defined according to size
extern double SIN_TAB[]; //Sine signal table
extern void Refresh_Data(struct compx *xin, int id, double wave_data);
extern void create_sin_tab(double *sin_t);
extern void FFT(struct compx *xin);
extern void Get_Result(struct compx *xin, double sample_frequency);
#endif
Usage Method
In FFT.h, modify FFT_N to 16, define the number of points for Fourier transform. Since the FFT transformation is normalized, the entire result table is symmetric except for the DC component at 0Hz. If the number of points is 16, we only need to look at the first 8 points. Therefore, the number of points for Fourier transform can be determined according to your pixel count in the long direction of the screen. For example, a 128×64 screen can consider using 256 points for FFT. Here I am using an 8×8 LED dot matrix screen to display, so I use 16 points for FFT.
Before computation, the create_sin_tab(SIN_TAB) function should be called to establish the sine signal table. After that, the lookup method will be used to calculate the sine value, speeding up the computation.
After using Refresh_Data(Compx, i, wave_data) to fill in the data,
call FFT(Compx) to complete the transformation.
Use Get_Result(Compx, Sample_Frequency) to calculate the modulus of the transformed result, stored in the real part of the complex number, the frequency stored in the imaginary part, valid data is the first FFT_N/2 numbers.
#define Sample_Frequency 800 //Sampling frequency 800Hz #define Frequency 100 //Test signal 100Hz
for (i = 0; i < FFT_N; ++i) //Use Refresh_Data(Compx, i, wave_data) to fill in data, here establish a 100Hz square wave test signal { if (sin(2 * PI * Frequency * i / Sample_Frequency) > 0) Refresh_Data(Compx, i, 1); else if (sin(2 * PI * Frequency * i / Sample_Frequency) < 0) Refresh_Data(Compx, i, -1); else Refresh_Data(Compx, i, 0); }
create_sin_tab(SIN_TAB); //Establish the sine signal table, after that will use the lookup method to calculate the sine value, speeding up computation FFT(Compx); //Fast Fourier Transform Get_Result(Compx, Sample_Frequency); //Calculate the modulus of the transformed result, stored in the real part of the complex number, frequency stored in the imaginary part, valid data is the first FFT_N/2 numbersEffect

Method to Calculate Frequency:
The sampling frequency is 800Hz, with a total of 16 points, thus one grid = 800Hz / 16 = 50 Hz.
As shown in the figure, there are peaks in the third and seventh grids, corresponding to frequencies of 2 x 50Hz = 100Hz and 6 x 50Hz = 300Hz. This result has been calculated by the Get_Result function and stored in the imaginary part of the original array.
Performance
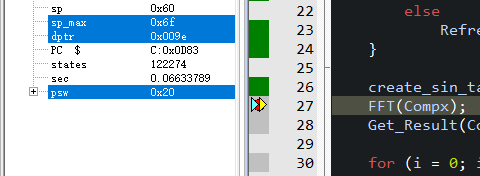
Crystal oscillation frequency 11.0592MHz 6T mode (22.1184MHz 12T)
Under simulation, it takes approximately 0.13222819 – 0.06633789 = 0.0658903 (s)
This means that it takes 65.8903 ms for a 16-point FFT transformation on a 51 microcontroller with a crystal frequency of 11.0592MHz 6T.

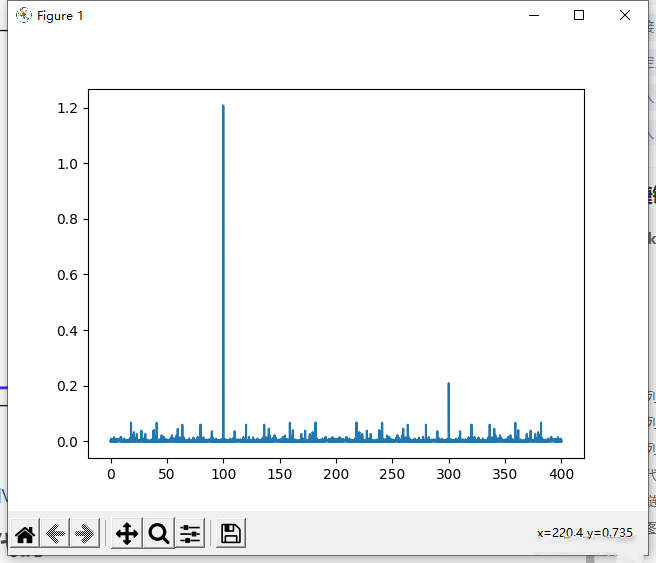
Using the same program, the results of using Vs 2015 to run 65536 points:
Results of using Python to calculate 800 points:
Source: The most detailed tutorial on implementing Fast Fourier Transform (FFT) using Python (scipy and numpy) — LoveMIss-Y
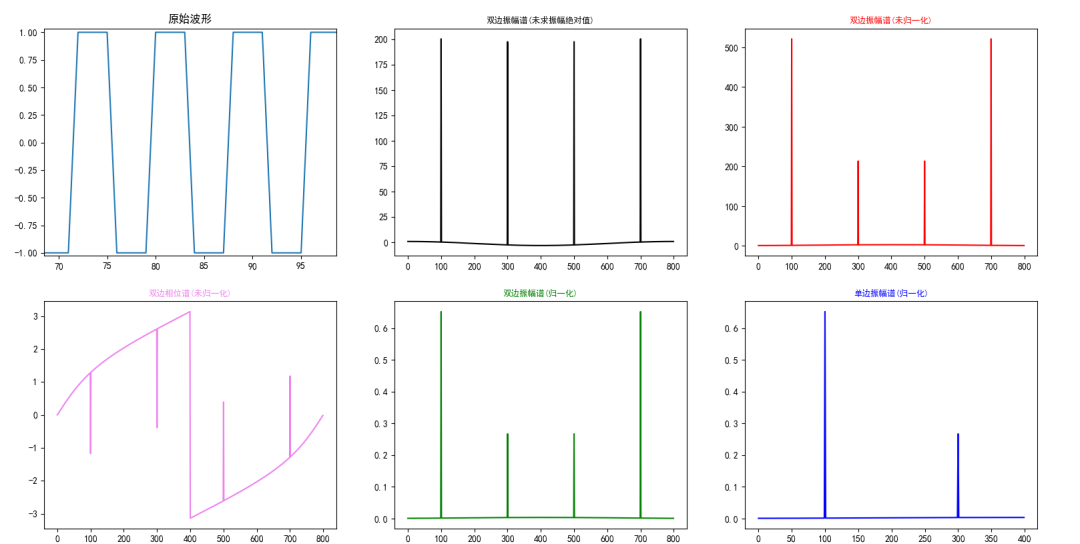
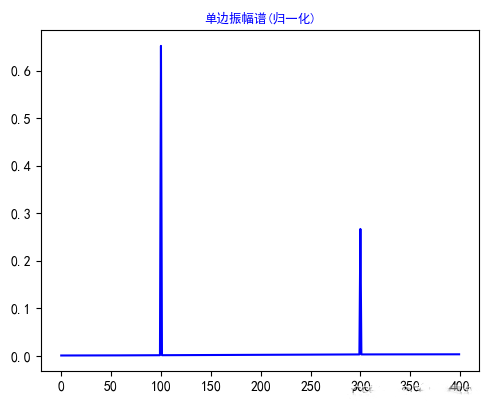
Other Code Parts
For the dot matrix screen part code, see [51 Microcontroller Quick Start Guide] 2.4: IO Expansion (Serial to Parallel) and LED Dot Matrix Screen.
main.c
#include <REGX52.H>#include "intrins.h"#include "stdint.h"#include "FFT.h"#include <math.h>#include "HC74595.h"
void main(void){ uint8_t i, j; double Largest = 0;
#define Sample_Frequency 800 //Sampling frequency 800Hz #define Frequency 100 //Test signal 100Hz
for (i = 0; i < FFT_N; ++i) //Use Refresh_Data(Compx, i, wave_data) to fill in data, here establish a 100Hz square wave signal { if (sin(2 * PI * Frequency * i / Sample_Frequency) > 0) Refresh_Data(Compx, i, 1); else if (sin(2 * PI * Frequency * i / Sample_Frequency) < 0) Refresh_Data(Compx, i, -1); else Refresh_Data(Compx, i, 0); }
create_sin_tab(SIN_TAB); //Establish the sine signal table, after that will use the lookup method to calculate the sine value, speeding up computation FFT(Compx); //Fast Fourier Transform Get_Result(Compx, Sample_Frequency); //Calculate the modulus of the transformed result, stored in the real part of the complex number, frequency stored in the imaginary part, valid data is the first FFT_N/2 numbers
for (i = 0; i < FFT_N / 2; ++i) //Process the calculation results into images { if(Compx[i].real > Largest) Largest = Compx[i].real; } for(i = 0; i < 8; ++i) { for(j = 0; j < (uint8_t)((Compx[i].real / Largest) * 8 + 0.5); ++j) Mat[8 - j - 1][i] = 1; }
while(1) { imshow(Mat); //Display image }}Copyright statement: This article is the original article of CSDN blogger “Yuan Suan Oxyberyllium”, following the CC 4.0 BY-SA copyright agreement, please reprint with the original source link and this statement. Original link: https://blog.csdn.net/weixin_44457994/article/details/121238658
[Download] Multisim Simulation 100 Examples.rar
