

Click the blue text above to follow us



1 Vehicle Routing Problem


In equations (9)~(12), ti is the time the delivery vehicle arrives at demand point i; cij is the transportation cost from demand point i to demand point j; wi and pi are the waiting cost and penalty cost per unit time for the delivery vehicle arriving early or late at demand point i, respectively. In this mathematical model, each demand point has a delivery vehicle, and each demand point can only be served by one logistics delivery vehicle; at the same time, the sum of the demand at the demand points on the same delivery route should not exceed the maximum load of the logistics delivery vehicle.
1. Introduction
With the rapid development of economic globalization and e-commerce, logistics delivery has become increasingly important in daily life and business activities. The Vehicle Routing Problem (VPR) is a core issue in logistics delivery, and its research is significant for improving logistics efficiency and reducing costs. This article will introduce the method and implementation of solving the VPR problem based on the Simulated Annealing (SA) algorithm.
2. Overview of the Vehicle Routing Problem (VPR)
The VPR is a classic combinatorial optimization problem that primarily studies how to optimize vehicle routes to minimize total transportation costs or reduce total transportation time. In the VPR, each vehicle has one or more routes, with several nodes (customers or delivery points) on each route, and the distances between nodes and the demand at each node are known. The goal is to find the optimal path that minimizes the total transportation cost or the total transportation time for all vehicles.
The mathematical model of the VPR typically includes an objective function, constraints, and variables. The objective function usually aims to minimize total transportation costs or total transportation time, while constraints include vehicle capacity limits, time window limits, and vehicle route length limits. Variables include the demand at each node, distances between nodes, and vehicle routes.
3. Introduction to the Simulated Annealing Algorithm (SA)
The Simulated Annealing algorithm is a random optimization algorithm based on the Monte Carlo iterative solving strategy, drawing on the similarity between the annealing process of solid materials in physics and general combinatorial optimization problems. The algorithm utilizes the Metropolis algorithm and appropriately controls the cooling process to achieve simulated annealing, thereby solving global optimization problems.
The core idea of the Simulated Annealing algorithm is to perform a random walk in the search space (i.e., randomly select points) and then use the Metropolis sampling criterion to gradually converge the random walk to a local optimal solution. The temperature is a crucial control parameter in the Metropolis algorithm, which can be considered to control the speed of the random process moving towards local or global optimal solutions.
4. Implementation of Solving the VPR Problem Based on Simulated Annealing Algorithm
-
Problem Definition:
-
Input: Distance matrix between nodes, demand at each node, vehicle capacity limits, time window limits, etc.
-
Output: Optimal vehicle path that minimizes total transportation costs or total transportation time.
Algorithm Steps:
-
Initialization: Set initial temperature T, cooling rate, number of iterations, etc., and generate an initial solution (i.e., initial vehicle path).
-
Iteration Process: At the current temperature, perform neighborhood search on the current solution to generate a new solution. Use the Metropolis criterion to determine whether to accept the new solution. Repeat this process until the number of iterations at the current temperature is reached.
-
Cooling: Reduce the temperature T according to the cooling rate, repeating the iteration process until the temperature reaches the termination condition.
-
Output Optimal Solution: The current solution at the termination of the algorithm is the approximate optimal solution obtained.
Key Technologies:
-
Neighborhood Search Strategy: Operations such as swapping, reversing, and inserting to generate new solutions.
-
Metropolis Criterion: Determines whether to accept a new solution based on the difference in objective function values between the current and new solutions and the temperature T.
-
Cooling Strategy: Controls the cooling process of temperature T to ensure the algorithm converges to the global optimal solution.
5. Implementation Results and Analysis
By implementing the VPR problem solution based on the Simulated Annealing algorithm in MATLAB, the running results are displayed. The results are analyzed to evaluate the performance and effectiveness of the algorithm. Comparisons can be made between running results under different parameter settings to optimize algorithm parameters and improve solution quality.
6. Conclusion and Outlook
This article introduced the method and implementation of solving the Vehicle Routing Problem (VPR) based on the Simulated Annealing algorithm. Through MATLAB code implementation and result analysis, the effectiveness and feasibility of the algorithm were verified. Future research could further explore the optimization and improvement of the algorithm and its application in more complex logistics delivery scenarios.



2 Running Results
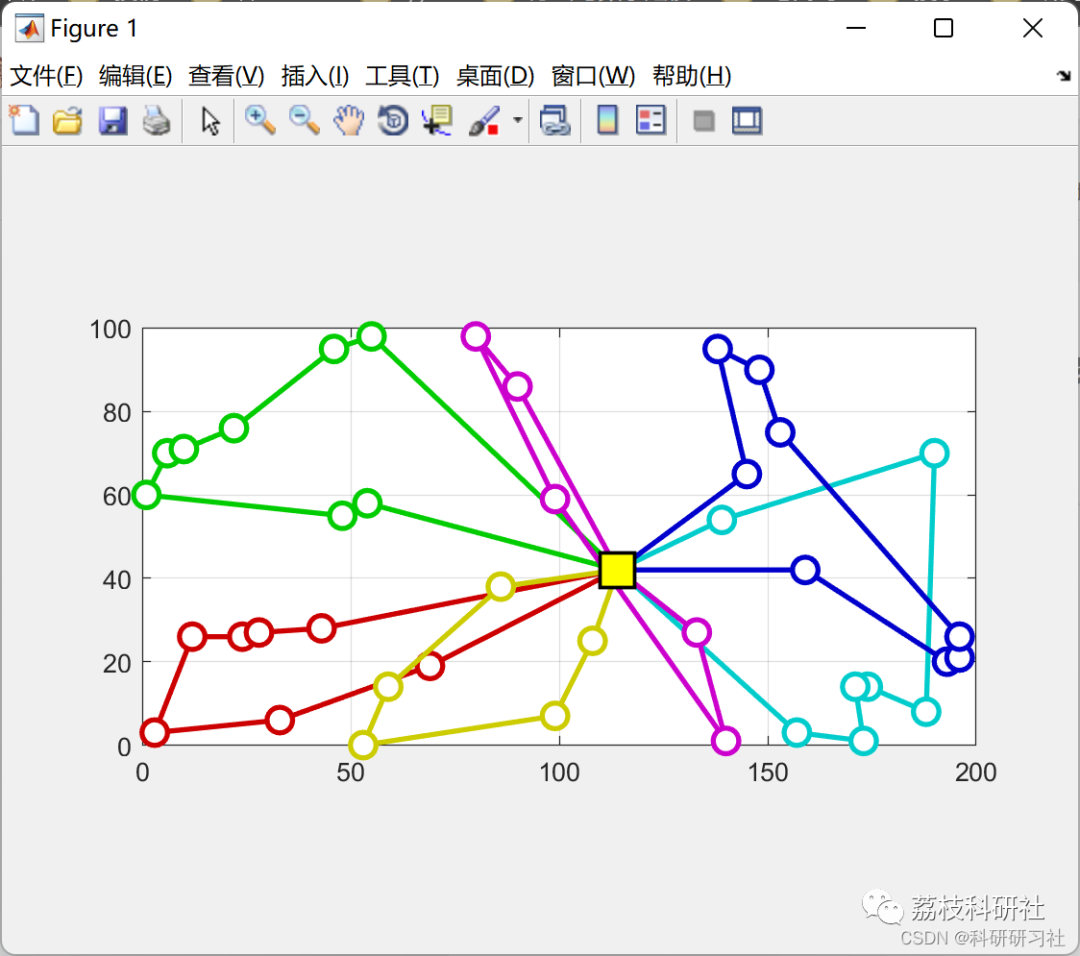
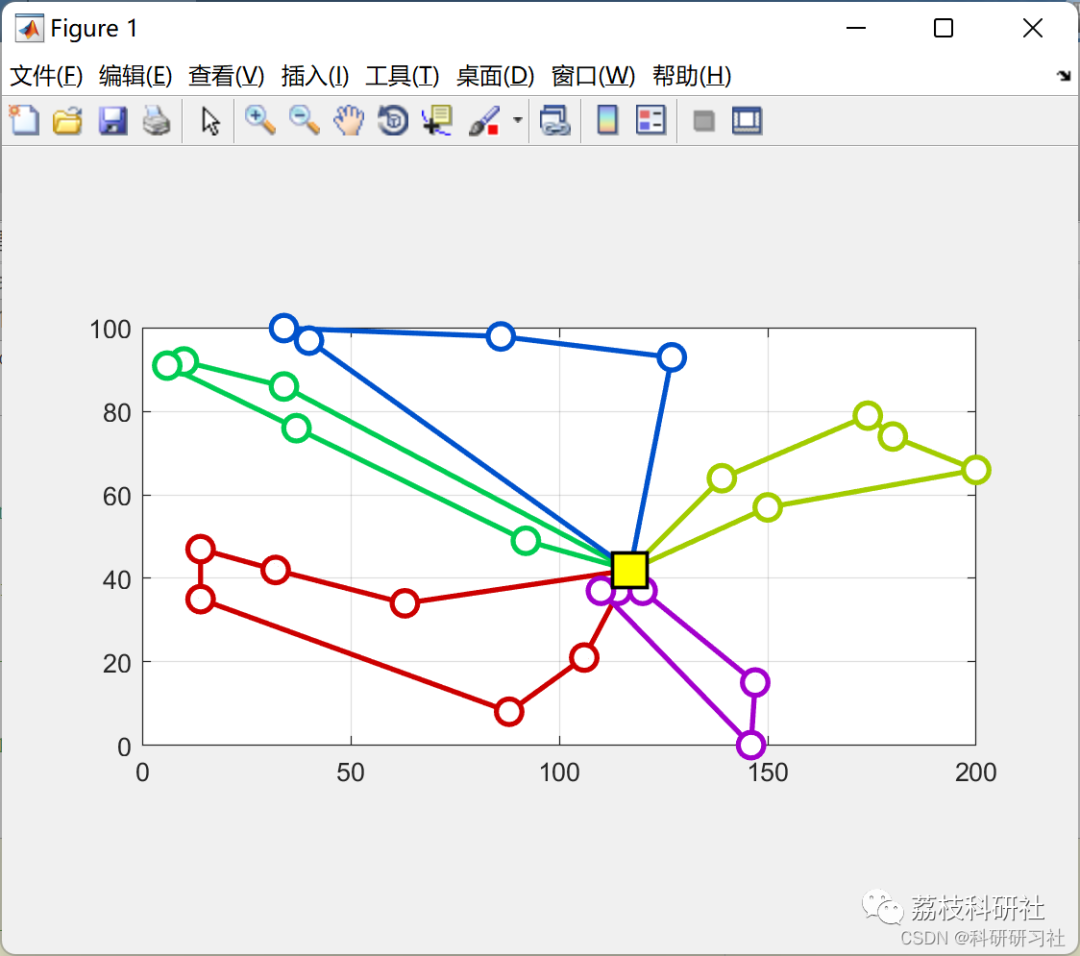
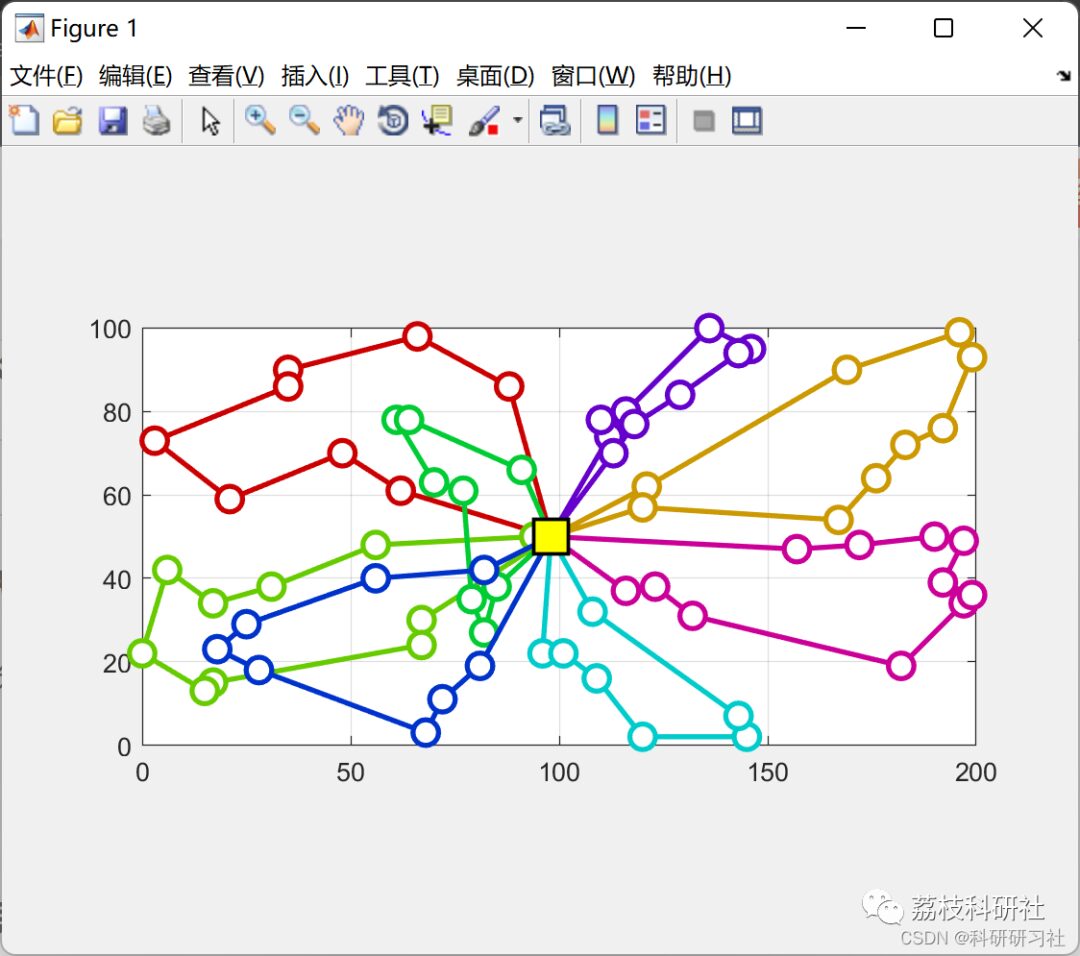
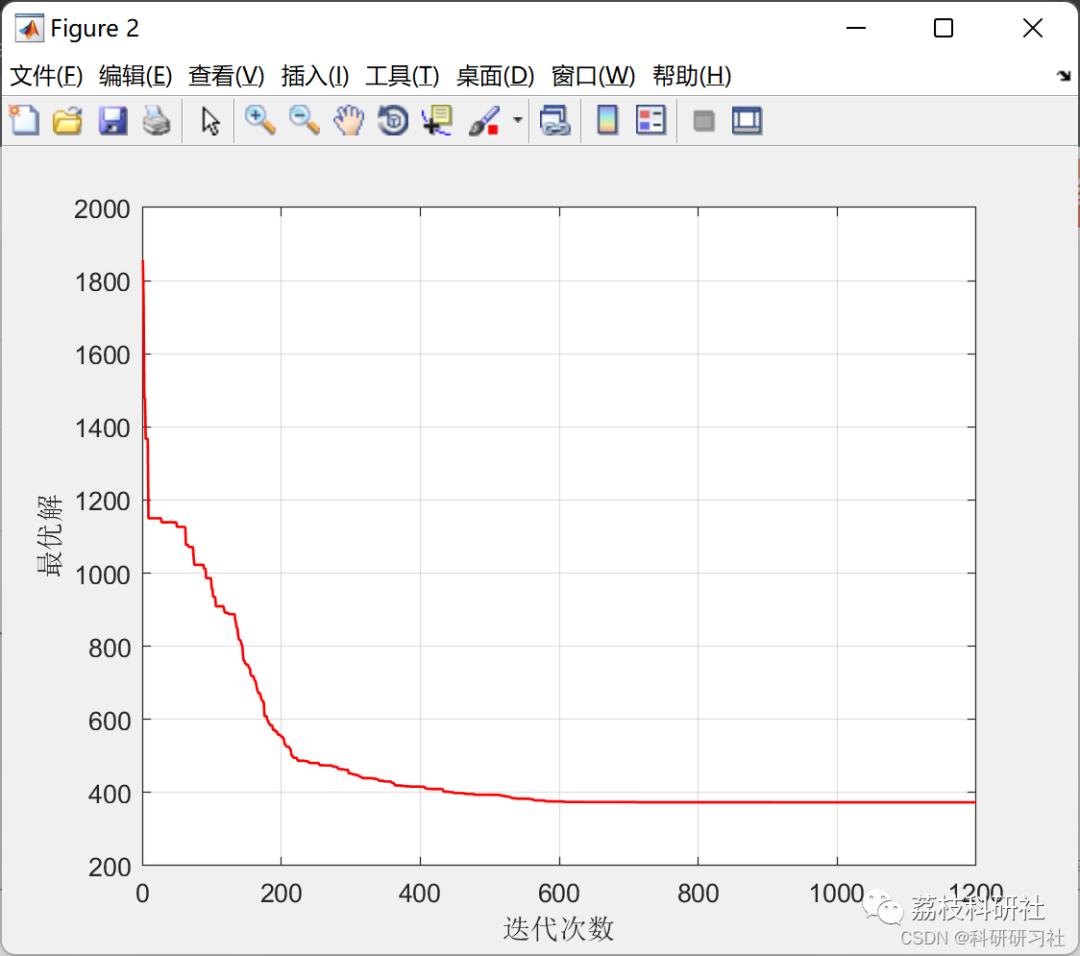
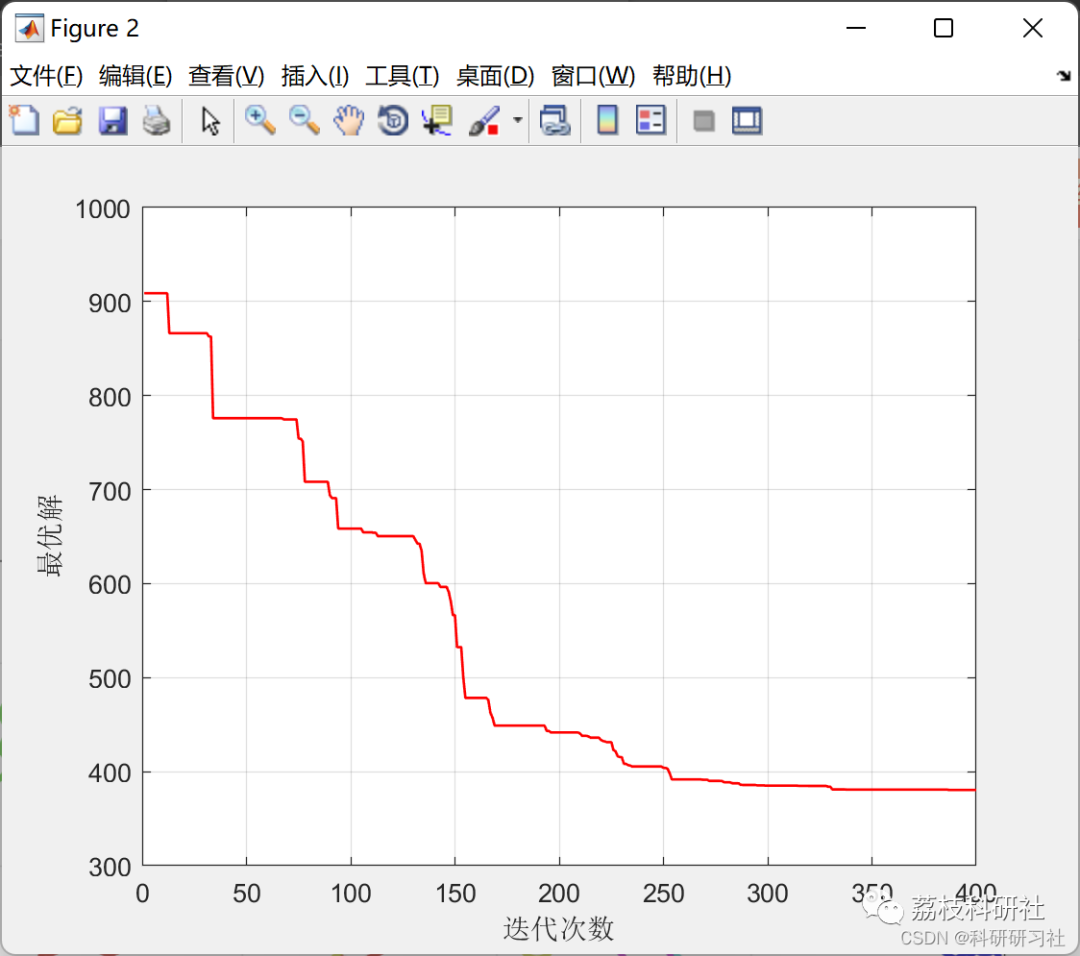


3 References
[1] Wu Huijun. Research on Vehicle Delivery Logistics Path Optimization Based on Grey Wolf Algorithm [J]. Journal of Anyang Normal University, 2021(2):36-40
[2] Tang Yan, Zhang Jinjun. Logistics Vehicle Delivery Path Planning Based on Improved Whale Optimization Algorithm [J]. Journal of Longdong University, 2021, 32(5):6-10



4 MATLAB Code