Breaking News! Breaking News!
The electronics technology and craft now have a video channel!
Welcome everyone to scan the code to check us out ☞
Only by persisting in learning can we continue to grow!
Resistors are quite common in our work, and we should not underestimate these inconspicuous components, as they hold a lot of knowledge.
Surface Mount Resistors (SMD Resistors), also known as chip fixed resistors, are resistors designed for surface mounting.
These SMD resistors are typically much smaller than traditional resistors, thus occupying significantly less space on the circuit board.

The SMD part of surface mount resistors refers to surface-mounted devices that can be directly installed onto PCB circuit boards using “Surface Mount Technology” (SMT).
The invention of surface mount technology has not only reduced the size of components but also significantly shortened the manufacturing time of circuits.
SMD resistors are typically used only in professionally manufactured PCBs.
For most DIY circuits, the more classic “through-hole” technology resistors are used.
The reason for using through-hole resistors is that they are easier to install and do not require specialized equipment like SMD resistors.
SMD Resistor Calculator
If you want to quickly find the value of your SMD resistor, you can use an SMD resistor calculator.
SMD Resistor Codes
When you see an SMD resistor, the first thing you will notice is that they do not use the color band system like “through-hole” resistors.
The reason is that there is not enough space on the smaller SMD resistor packages to print color band codes.
To address this, three new coding systems have been proposed, two of which are defined according to the IEC 60062:2016 standard: a four-digit system and a three-digit system.
The third is the “EIA-96” numbering system designated by the Electronic Industries Alliance, which ceased operation in 2011.
Below, we will introduce how to utilize these systems step by step.
Three-Digit SMD Resistor Code System
In this system, the first two digits define the resistance value. In this numbering system, the third digit also represents the multiplier for resistance values greater than 10 ohms.
When an SMD resistor is below 10 ohms, the letter “R” is used to define the position of the decimal point. For example, an 8R3 SMD resistor defines a resistance value of “8.3” ohms.
Unlike the color code system, the multiplier in this numbering system represents the power of ten. For example, a 273 resistor represents 27×10^3.
Example of Calculating a Three-Digit SMD Code
In this example, assume there are four SMD resistors with three-digit codes: one 901, one 3R4, one 313, and one R34.
Example 1 – 901
For the first SMD resistor 901, take the first two digits as the base value of the resistor. The first two digits give us a base value of “90”.
Then, multiply this base by 10 raised to the power of the last digit in the code.
R = 90 x 10^1
R = 900
Thus, we can calculate that the resistance of our first SMD resistor is 900 ohms.
Example 2 – 3R4
Now for the second resistor 3R4, no multiplication is needed.
All that needs to be done is to write down the value and place the decimal point as indicated by the “R” in the code.
R = 3R4
R = 3.4
So, we can determine that the resistance of the second resistor is 3.4 ohms.
Example 3 – 313
For the third resistor (313), we need to handle it like the first example.
First, take the first two digits, so the base resistance value of the SMD resistor is 31.
Then, take the last digit as the power of ten. Now we need to multiply 31 by 10 raised to the power of 3.
R = 31 x 10 ^ 3
R = 31,000
We can calculate that the actual resistance of this resistor is 31,000 ohms or 31K ohms.
Example 4 – R34
Now for the fourth and final resistor (R34).
This SMD resistor is similar to our second example, but the position of the decimal point is moved to the front.
R = R34
R = .34
Using this, we can quickly determine that the resistance of this SMD resistor is 0.34 ohms.
Summary
- All three digits are pure numbers, the first two remain unchanged, and the last digit indicates the number of zeros;
For example: 901=900 313=31000
- In the three digits with an “R”, the position of “R” indicates the position of the decimal point.
Four-Digit SMD Resistor Code System
The four-digit SMD resistor code system is similar to the three-digit system, with the only difference being the addition of one digit.
In the four-digit SMD resistor code system, the first three digits represent the base resistance value. The fourth digit represents the power of ten.
Example of Calculating Four-Digit SMD Code
We will illustrate this with two different resistors.
The resistors are 4402 and 95R21 SMD resistors.
Example 1 – 4402
First, we need to take the first three digits from the written value of the resistor, noting that the base resistance value is 440 ohms.
From this same value, we can derive the multiplier from the last digit of the resistance value, which is 2.
Then, we need to multiply our base value of 440 by 10 raised to the power of 2.
R = 440 * 10^2
R = 44,000
We can calculate that the value of the SMD resistor is 44,000 ohms.
Example 2 – 95R21
The second example of a four-digit SMD resistor value is 95R21.
Since the value contains the letter “R”, we immediately know that we do not need to perform multiplication.
All we need to do is replace the “R” with a decimal point to find the actual resistance value of the sampled resistor.
R = 95R21
R = 95.21
Thus, we find that the resistance value is 95.21 ohms.
Summary
Similar to the three-digit SMD resistor code system.
EIA-96 System
The third and final system used to calculate the resistance value of SMD resistors is the EIA-96 system. It uses a three-digit system where the first two digits represent a value from the E96 series of resistors.
We have a table that shows the corresponding value for each code among the 96 possible codes in the E96 series. You can find this table below.
In the EIA-96 system, the third digit is always a letter representing the multiplier. You can use the table below to match the letter with the multiplier value.
EIA-96 Multiplier Table
We can use this table to quickly calculate the multiplier for SMD resistors using the EIA-96 system.
All we need to do is look up the last letter and multiply the value by the corresponding multiplier.
| Code | Multiplier |
|---|---|
| Z | 0.001 |
| Y / R | 0.01 |
| X / S | 0.1 |
| A | 1 |
| B / H | 10 |
| C | 100 |
| D | 1,000 |
| E | 10,000 |
| F | 100,000 |
EIA-96 Code Value Table
Since the EIA-96 numbering system relies on the values of the E96 series, we must use a table like this to find the actual base resistance value.
Use the table below to look up the first two digits of our EIA-96 SMD resistor to find its base resistance value.
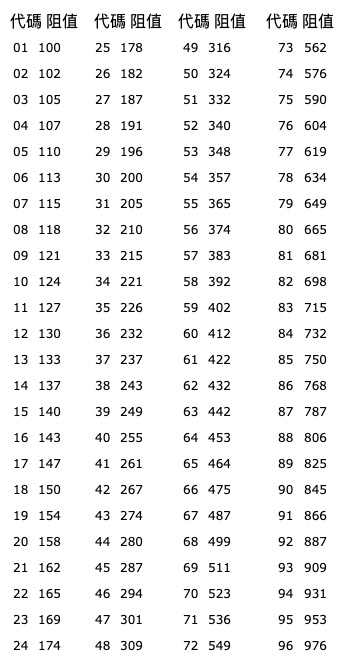
Examples of Calculating EIA-96 SMD Resistors
Calculating the resistance value of EIA-96 SMD resistors is slightly more complex than for three or four-digit resistors.
To help everyone understand how to calculate the resistance value of SMD resistors based on EIA-96, we will demonstrate three different resistor examples.
These EIA-96 resistance value examples are 33A, 11Y, and 67C.
Example 1 – 33A
The first resistor example to study is the 33A EIA-96 SMD resistor.
The first step is to calculate the base resistance value. To do this, we must take the first two digits of the resistor.
In this example, the value is 33. Looking up this code in the table above, we can calculate that its resistance value is 215.
Next, we need to calculate the multiplier. Again, looking up the value of A in the multiplication table, we find that the multiplier is 1.
Since the multiplier is 1, the resistance value of the 33A EIA-96 SMD resistor is simply 215.
Example 2 – 11Y
The second example’s resistor is slightly more complex because it uses a multiplier, not just multiplying the value by 1.
This second example’s SMD resistor value is 11Y.
First, we need to calculate the value of the first two digits.
Looking up in the table, we see that 11 corresponds to a base resistance of 127.
Now that we know the base resistance of the SMD resistor is 127, we can continue to calculate the multiplier.
Referring to the multiplication table, we see that the letter Y indicates we need to multiply this number by 0.01. This multiplier value is equivalent to dividing the number by 100.
Now that we know the multiplier, we can calculate the actual resistance of the 11Y resistor by multiplying 127 by 0.01.
R = 127 x 0.01
R = 1.27
From this value, we can determine that the resistance of the 11Y resistor is 1.27 ohms.
Example 3 – 67C
Now let’s look at the third EIA-96 SMD resistor example, the 67C resistor.
The first step is to take the first two digits of the resistor’s value, which in this case is 67.
As with the previous two examples, we need to look up 67 in the code table to find its value, which is 487.
Next, we need to calculate the multiplier. Referring to the letter H in the table, we find that the multiplier is 100.
Using this multiplier, we multiply the base resistance of 487 by the multiplier of 100 to calculate the actual resistance of the SMD resistor.
R = 487 x 100
R = 48,700
From these values, we can calculate that the final resistance of our sample SMD resistor is 48,700 ohms.
We hope that by now, you have learned how to read the values of SMD resistor codes and have a basic understanding of these types of resistors.

Click the blue text to view recent exciting articles
➤ Simple explanation of process management
➤ Master 8 points to be a good process engineer
➤ Knowledge structure that modern electronic process engineers should possess
➤ In-depth learning - process scheme design and management
➤ Practical - electronic production process training knowledge
➤ Super practical - manual soldering process video
➤ Practical application of the seven major methods of IE
➤ Three major items to improve electronic process management
➤ PCB process design specifications that electronic engineers should know
➤ Learning - Huawei supply chain management
➤ Key points for PE improvement (golden rules)
➤ To do a good job in process management, the following three dimensions must be considered.
➤ Thread fastening force process standards used in electronic assemblies
99% of people who read this article scanned the QR code below
☟ ☟ ☟
If you find it useful, please share and take a look.