1.Concept of Symmetric Encryption Algorithms
Both parties in communication can use a secure communication system to shield and protect the messages that need to be sent. The message to be sent by the sender is called plaintext, and the plaintext is transformed into a meaningless random message called ciphertext. This transformation process is called encryption; the reverse process, recovering the original plaintext from the ciphertext, is called decryption. During the encryption and decryption processes, it needs to be carried out under the control of a key. According to the similarities and differences between the encryption key and the decryption key, cryptographic systems are divided into single-key systems and double-key systems. A single-key system has the same encryption key and decryption key, known as a symmetric encryption system, while a double-key system has different encryption and decryption keys, known as an asymmetric encryption system.
The origin of symmetric encryption algorithms can be traced back to the classical cryptography era in the late 19th century. Classical cryptography has two types: simple substitution ciphers, which replace each letter in the plaintext alphabet with the corresponding letter in the ciphertext alphabet, and correspond one-to-one using a plaintext-ciphertext correspondence table for encryption and decryption, such as the Caesar cipher and affine cipher; and multiple substitution ciphers, which establish multiple mappings from plaintext letters to ciphertext letters, each mapping corresponding to a simple substitution cipher, making it more secure than simple substitution ciphers, such as the Vigenère cipher. Classical ciphers can be attacked by frequency analysis, and modern computing power can easily break them. Therefore, more complex cryptographic methods are needed to protect messages during communication.
Symmetric encryption systems can be divided into block ciphers and stream ciphers according to the different methods of encrypting plaintext messages. Block cipher systems encrypt plaintext by dividing it into multiple fixed-length plaintext blocks, while stream cipher systems encrypt only a single bit of plaintext at a time.
2.Development History of Symmetric Encryption Algorithms
The design of block cipher algorithms originated from a paper published by Claude Shannon in the Bell System Technical Journal in 1949 titled “Communication Theory of Secrecy System,” in which he proposed the principles of “confusion” and “diffusion” for the design of block cipher algorithms. In the late 1970s, the U.S. National Bureau of Standards announced the Data Encryption Standard (DES) algorithm, sparking a wave of public research into block cipher algorithm design. In the late 1990s, the U.S. AES program and the European NESSIE program at the beginning of this century greatly promoted the research of block cipher theory and applications. The Rijndael algorithm was selected as the U.S. Advanced Encryption Standard in the AES program, while Camellia, MISTY1, SHACAL-2, and AES were established as the block cipher standard algorithms for Europe in the new century in the NESSIE program. In 2006, China announced its first national block cipher algorithm standard SMS4, which is now known as the commercial cipher algorithm SM4, followed by the emergence of unpublished block cipher algorithm standards such as SM1 and SM7. Today, there are numerous block cipher algorithms [1], such as variations of DES, IDEA algorithm, SAFER series algorithms, RC series algorithms, Skipjack algorithm, Rijndael algorithm, FEAL series algorithms, REDOC series algorithms, LOKI series algorithms, CAST series algorithms, Khufu, Khafre, MMB, 3-WAY, TEA, MacGuffin, SHARK, BEAR, LION, CA.1.1, CRAB, Blowfish, GOST, SQUARE, MISTY, FOX, SM1, SM4, SM7, SSF33, etc.
With the development of the Internet of Things, micro devices such as wireless sensors and RFID chips have been widely used. Due to the limited computational resources of micro devices and the need to ensure information security, lightweight block cipher algorithms have emerged. The first lightweight block cipher algorithm appeared in 1996, named DESL, which was designed to be lightweight based on DES, aimed at reducing the complexity of gate circuits in serial hardware architectures. Subsequently, many lightweight block cipher algorithms appeared, such as HIGHT, PRESENT, MIBS, KATAN&KTANTAN, LBlock, Hummingbird, SIMON, etc.
The earliest form of stream ciphers is the Vernam cipher. In 1949, Claude Shannon proved that the one-time pad cipher is theoretically unbreakable and absolutely secure, and the one-time pad scheme became the basis for the development of stream ciphers. The development of stream cipher systems has been constrained due to significant difficulties in key management, limiting their application to high-security situations where stream ciphers are adopted, and the design of stream ciphers is generally not public. Due to the difficulties associated with true random sequences in key management, stream ciphers based on pseudo-random sequences have developed. Stream ciphers are simple to implement, have high encryption and decryption efficiency, and the key stream sequence can be easily generated using circuits based on shift registers. Today, stream ciphers are also known as sequence ciphers, with typical sequence cipher algorithms including A5-1, RC4, ZUC, etc.

Currently, commonly used block cipher algorithms adopt iterative structures. Depending on the structure used by the algorithm, the main structures can be divided into Feistel structure, SPN structure, and Lai-Massey structure. In addition to these three mainstream structures, the overall structure also includes generalized (non) balanced Feistel structures, MISTY structures, and mixed-use structures. Currently, China’s commercial cipher algorithm SM4 adopts the generalized (non) balanced Feistel structure. Below, we will introduce the Feistel structure, SPN structure, and Lai-Massey structure, along with their advantages and disadvantages.
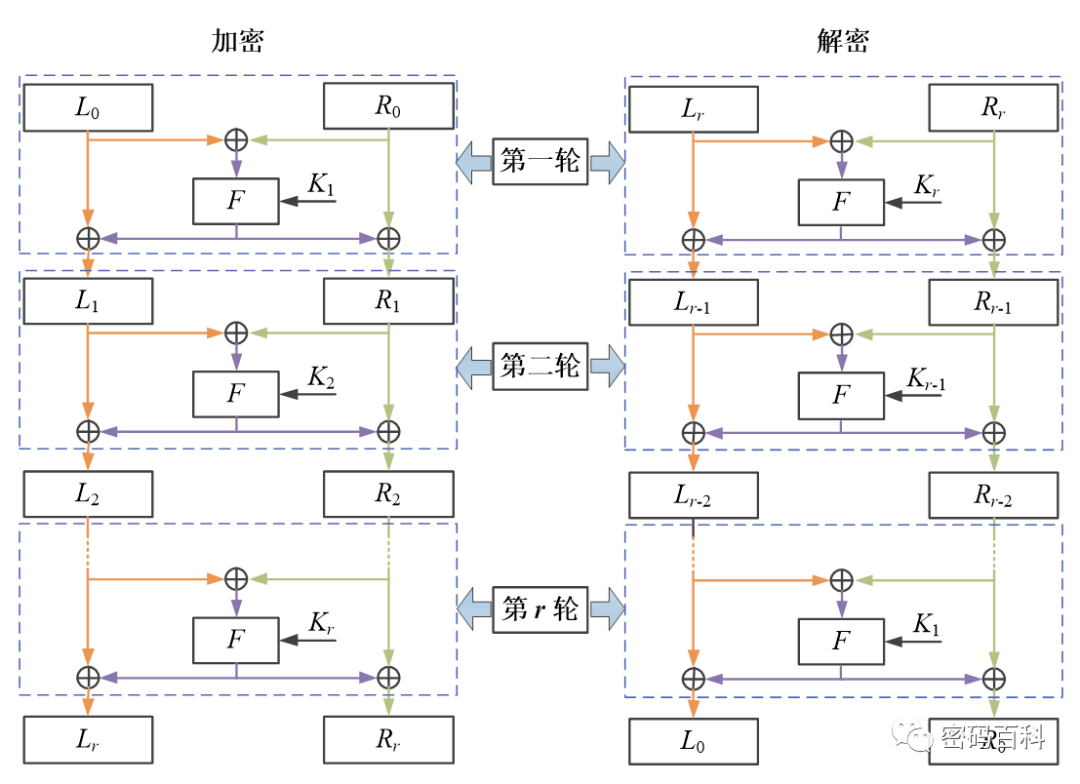
The Feistel structure was proposed by IBM’s Feistel and Tuchman in the late 1960s when designing the Lucifer block cipher algorithm. The DES algorithm uses the Feistel structure.
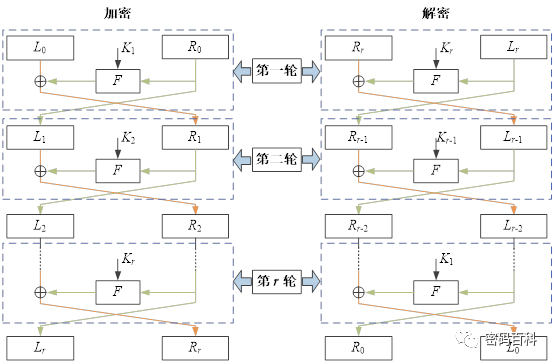
For a Feistel structure with a block length of 2n and r rounds, the plaintext is divided into two n-bit parts, L0 for the left part and R0 for the right part, and processed according to the rules given in Figure 1 for r rounds.
The iterative process is expressed by the following formula:
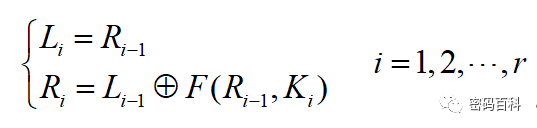
Where plaintext is M=L0R0, and the ciphertext result is the last round’s iterative result with the left and right parts swapped, i.e., C=RrLr. The round keys K1, K2,…, Kr are derived from the seed key K according to the key expansion scheme, and F is the round function. When using the Feistel structure for encryption, the order of the sub-keys used in each round is K1, K2,…, Kr, and the decryption process is the same as the encryption, but the order of the sub-keys is reversed, i.e., Kr, Kr-1,…, K1.
From Figure 1, it can be seen that the guarantee of the encryption and decryption being inverses of each other is provided by the Feistel structure itself and does not depend on the choice of F function. Therefore, the design of the F function must ensure sufficient “confusion” and “diffusion” of the n-bit bit string to be transformed.
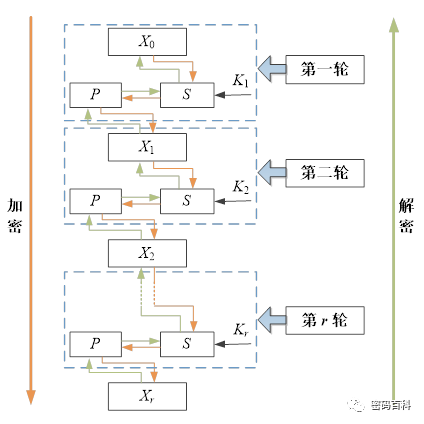
The iterative process is expressed by the following formula:
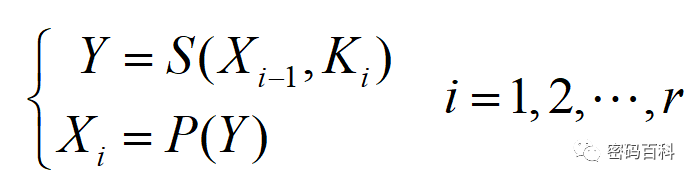
Where plaintext M=X0, ciphertext C=Xr, and the round keys K1, K2,…, Kr are derived from the seed key K according to the key expansion scheme. S is a reversible nonlinear function controlled by a round key, serving to provide “confusion,” and P is a reversible linear transformation serving to provide “diffusion.”
From Figure 2, it can be seen that the decryption of the SPN structure is the reverse of the encryption process, and typically, encryption and decryption do not have consistency, requiring the design of S transformation and P transformation to meet the reversibility conditions to ensure that the algorithm’s encryption and decryption are mutually inverse.
The Lai-Massey structure originates from the IDEA block cipher algorithm designed by Lai and Massey in 1990, then referred to as the Proposed Encryption Standard (PES). Serge Vaudenay abstracted the IDEA algorithm into a general cryptographic algorithm structure, naming it the Lai-Massey structure after its original designers.
For an r-round Lai-Massey structure with a block length of 2n, the plaintext is divided into two n-bit parts, L0 for the left part and R0 for the right part, and processed according to the rules given in Figure 3 for r rounds.
The iterative process is expressed by the following formula:
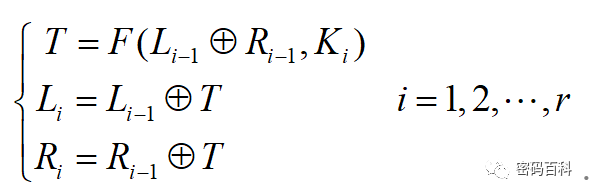
Where plaintext M=L0R0, ciphertext C=LrRr, and the round keys K1, K2,…, Kr are derived from the seed key K according to the key expansion scheme, and F is the round function. The Lai-Massey structure is similar to the Feistel structure, where the encryption and decryption processes only need to replace the order of the round keys used, and the guarantee of the encryption and decryption being inverses of each other is provided by the Lai-Massey structure itself, independent of the choice of F function. Therefore, the design of the F function is not constrained by the conditions of reversibility.
The Feistel structure’s encryption and decryption processes are consistent, which can save half the resources in implementation, but the Feistel structure only changes half of the data in each round, resulting in slower diffusion. In the design of Feistel structures, the F function is not constrained by reversibility, allowing for the use of “diffusion” and “confusion” ideas, as well as randomness.
The SPN structure has better diffusion, changing all data in one round, but the encryption and decryption processes of the SPN structure are typically inconsistent, consuming more resources in implementation. Additionally, designing a secure, key-controlled reversible nonlinear function S is quite challenging. In terms of security, the SPN structure is generally more secure than the Feistel structure.
The Lai-Massey structure combines the advantages of both Feistel and SPN structures, achieving consistency in encryption and decryption while changing all data in one round. The security of the Lai-Massey structure is comparable to that of the Feistel structure.
4Stream Cipher Algorithm Structure
The working principle of stream ciphers can be represented as shown in Figure 4. The key stream generator produces key streams that cannot be truly random. The security of stream ciphers needs to be assessed in terms of their period, randomness, and unpredictability.
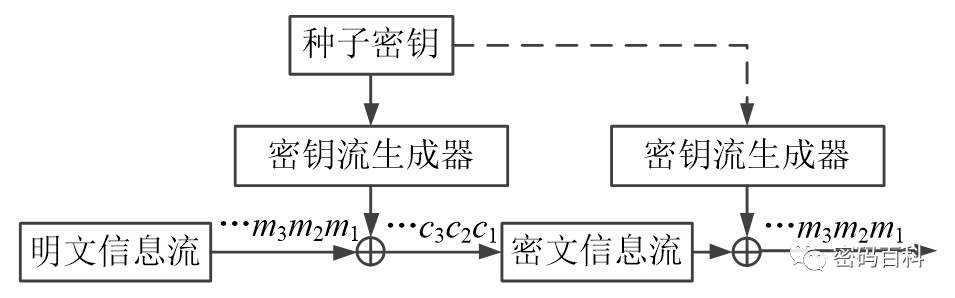
The periodicity of the key stream generator refers to the repetition of the key stream sequence starting from the T-th bit. From a security perspective, T needs to be sufficiently large; randomness refers to the statistical characteristics of the “0” and “1” in the key stream sequence being random; unpredictability means that analyzing the produced key stream sequence to deduce the entire sequence is computationally infeasible.
Currently, common methods for designing stream ciphers include those based on linear feedback shift registers, nonlinear feedback shift registers, using tables, constructing stream ciphers from block ciphers, and combinations of these methods.
Shift registers are a major component in generating key streams for stream ciphers. An n-stage feedback shift register over the finite field GF(2) consists of n binary memory elements and a feedback function f, as shown in Figure 5.
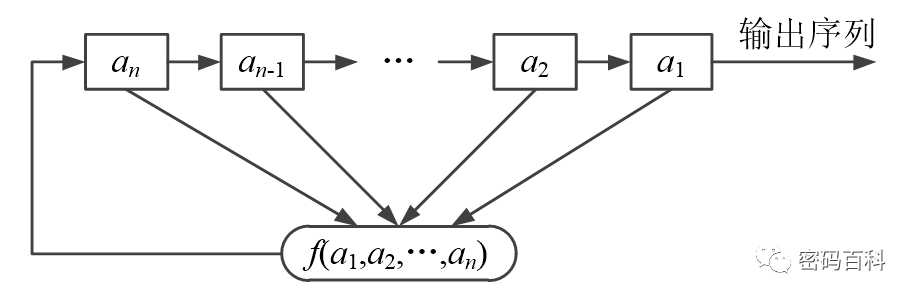
The initial state of the shift register is determined by the user. Based on the current state of the register a1,a2,…,an, the next state an is calculated as f(a1,a2,…,an). Whether the feedback function f is linear or nonlinear determines whether the shift register is a linear feedback shift register or a nonlinear feedback shift register.
When the feedback function f is linear, it can be expressed as
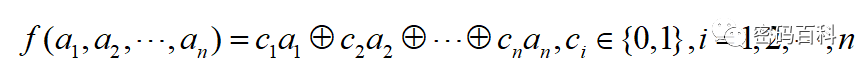
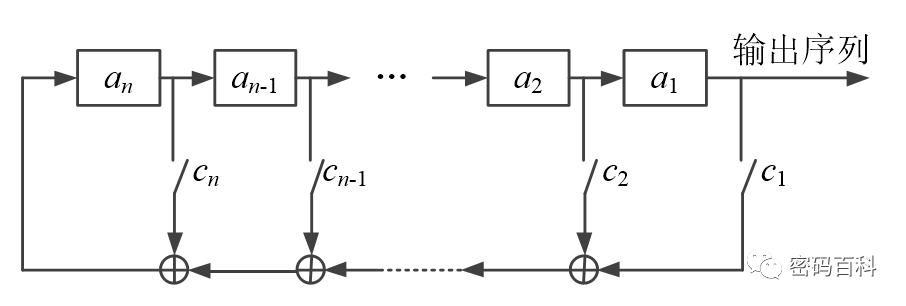
At this time, the shift register is called a linear feedback shift register (LFSR). LFSRs have advantages such as simplicity of implementation, speed, and mature theoretical foundations. The values of ci can be viewed as the off and on states of a switch. Figure 6 shows the n-stage linear feedback shift register over GF(2).
When the feedback function f is nonlinear, the shift register is referred to as a nonlinear feedback shift register. Compared to LFSRs, the binary sequence output by the key stream generator is more complex, has a larger period, and higher unpredictability.
Methods for constructing nonlinear sequences include the Geffe sequence generator, J-K flip-flop, Pless generator, and clock-controlled sequence generator.
The Geffe sequence generator consists of three LFSRs, where the output of one LFSR is used as a control generator, which can be understood as a single pole double throw switch. Its structure is shown in Figure 7. The Geffe sequence achieves a maximal period, and the distribution between 0 and 1 is generally balanced.
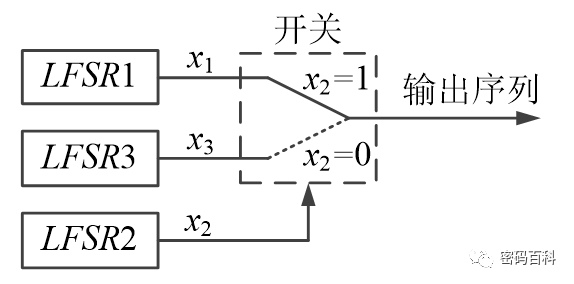
Its nonlinear combination function is
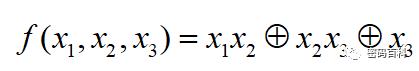
Where x1,x2,x3 are the outputs of the three LFSRs.
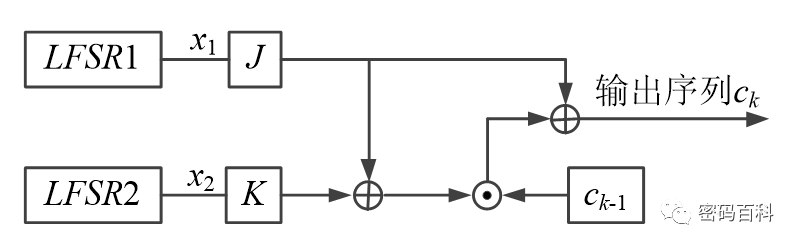
The J-K flip-flop consists of two LFSRs, represented by J and K, and its output sequence ck depends not only on J and K but also on the previous output ck-1. Its structure is shown in Figure 8.
Expressed with nonlinear functions as
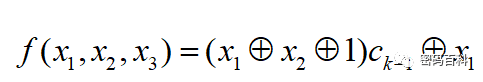
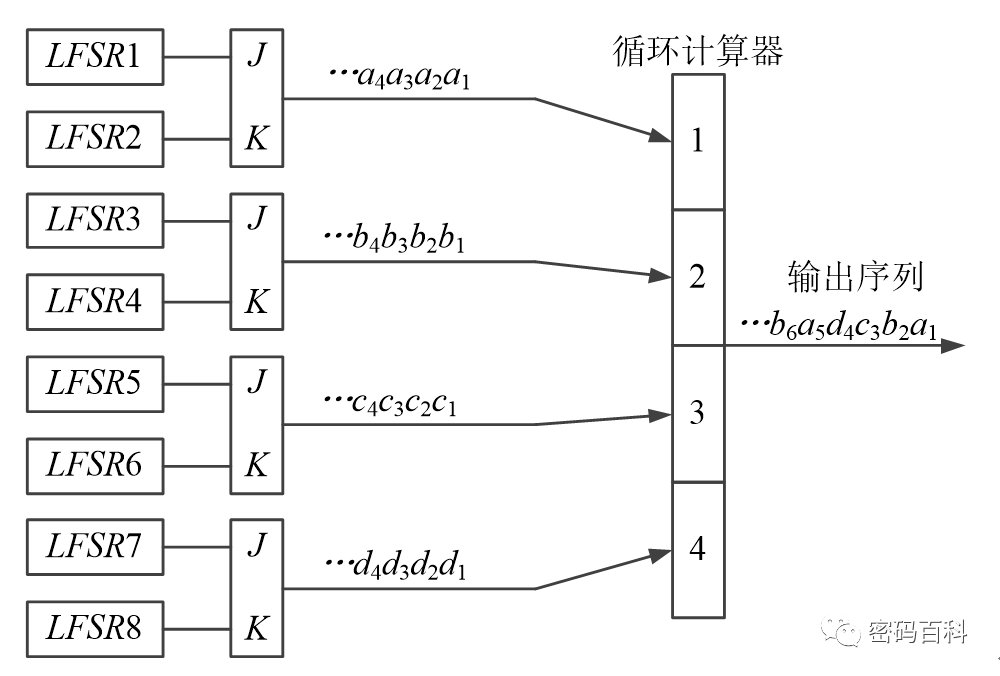
The Pless generator is a multi-path composite sequence scheme based on the J-K flip-flop, consisting of 8 LFSRs, 4 J-K flip-flops, and 1 cyclic counter. Its structure is shown in Figure 9.
The most basic scheme for a clock-controlled sequence generator is to use one LFSR to control the shift clock pulse of another LFSR. For example, when LFSR1 outputs 1, the shift clock pulse allows LFSR2 to shift once, generating the next bit; when LFSR1 outputs 0, the shift clock pulse cannot pass through the AND gate to affect LFSR2, so LFSR2 repeats the current output. More complex schemes can be constructed using the most basic clock-controlled sequence generator.
Secure block cipher algorithms with pseudorandomness can use the feedback output mode (OFB) and counter mode (CRT) of block algorithms as stream ciphers. For example: AES-256, Camellia, SHACAL2, etc.
Note: Reprinted with permission from Shenzhen Cryptography.
Follow/Subscribe to Us

