This article is a highlight from the Kanxue Forum.
Author ID on Kanxue Forum: techliu
The representation of basic data types in C++ is summarized in this section based on the book “C++ Disassembly and Reverse Engineering Techniques Revealed”, which also includes content from Chapter 2 on floating-point numbers from “Computer Systems: A Programmer’s Perspective”. For detailed content, please refer to the relevant chapters in the book.Integer Types
In a 32-bit computer, data is stored in the form of DWORD (double word).
Different integer types have different storage mechanisms. For example, the range of values that can be represented by unsigned integers is twice that of signed integers, and the representation of negative and positive numbers in signed integers is different.
Regardless of whether they are signed or unsigned, data is stored in memory in little-endian format, meaning that the high byte is stored at a high address and the low byte at a low address. Note that this is by byte, not by bit.
>>>>
1. Unsigned Integers
Unsigned integers in C++ are represented using the keyword unsigned int, occupying 4 bytes, with each bit representing a value. The range of representable values is: 0x00000000~0xFFFFFFFF, which corresponds to the decimal range: 0~4294967295.
When an unsigned integer is less than 32 bits, the remaining high bits are filled with 0 until the 4-byte memory space is filled.
Since every bit of an unsigned integer is used to represent a value, unsigned integers are stored in memory in their true value form.
>>>>
2. Signed Integers
Signed integers in C++ are represented using the keyword int, occupying 4 bytes. The highest bit of a signed integer is used to represent the sign, known as the sign bit, where a sign bit of 0 indicates a positive number, and 1 indicates a negative number.
Thus, only 31 bits are used to represent the value, with the range of representable values being: 0x80000000~0x7FFFFFFF,
corresponding to the binary representation: -2147483648~2147483647.
Careful readers may notice a problem: the highest bit is the sign bit, 0x80000000 corresponds to the binary 1000 0000 0000 0000 0000 0000 0000 0000, which seems to indicate -0, right?
First, let’s discuss how negative numbers are stored in memory. Negative numbers are stored using two’s complement. Whether using two’s complement or one’s complement, both are derived from the original code.
The original code is the binary code with the leftmost sign bit unchanged, while the two’s complement is obtained by inverting the absolute value of the number’s original code and adding 1. Modern computers use two’s complement to represent negative numbers, which has the advantage of allowing addition or subtraction without needing different calculation methods based on the sign of the number.
When storing negative numbers in two’s complement form, if we do not consider 0x80000000, the smallest negative number should be 0x80000001, which, when inverted and added 1, gives the original code of 0x7FFFFFFF, thus 0x80000001 represents -2147483647.
Now looking at 0x80000000, it can represent both -0 and 0x80000001 – 1. Since there is no need to have two representations of 0, it is defined that 0x80000000 represents 0x80000000 -1, which is -2147483648.
In summary, the range for positive numbers is 0x00000000~0x7FFFFFFF, and for negative numbers, it is 0x80000000~0xFFFFFFFF.
Floating-Point TypesThe storage methods for floating-point types can be divided into two types:
1. Fixed-Point Real Number Storage Method
> The position of the decimal point is fixed. If a real number is stored in 4 bytes, 2 bytes are used to store the integer part, and 2 bytes are used to store the fractional part.
> Although the computational efficiency is high, it is inflexible; if the data exceeds 2 bytes, it cannot be stored.
2. Floating-Point Real Number Storage Method
> The position of the decimal point is not fixed. A few binary bits are used to represent the position of the decimal point, called the “exponent field”, while the remaining bits represent the “data field” and the “sign field”. During computation, the exponent field is extracted first, and then the data field is split to obtain the true value. For example, for 655.35, the exponent field stores 10 to the power of -2, and the data field stores 65535. When computed, the true value is obtained.
> This method has the opposite advantages and disadvantages compared to fixed-point.
For modern computers, with the continuous upgrades of CPUs, the floating-point real number storage method has become widespread, with fixed-point storage only seen in some embedded devices.
In C++, there are two ways to represent floating-point numbers: “float” uses 4 bytes to represent a floating-point number, while “double” uses 8 bytes.
Floating-point operations do not use general-purpose registers but are processed using floating-point registers provided by the floating-point coprocessor.
In VC++ 6.0, before using floating-point numbers, the floating-point registers must be initialized to function correctly. If not initialized, an error will occur, for example:
int mian(void)
{
// When floating-point numbers are not used,
int nInt = 0;
// In VC++ 6.0, entering a decimal will cause an error due to uninitialized floating-point registers
scanf("%f", &nInt);
return 0;
}
If a floating-point type variable is defined anywhere in the code, the floating-point register will be initialized, and no error will occur.
Here is another piece of code to observe the running results:
#include <stdio.h>
void main(void){
int num=9; /* num is an integer variable, set to 9 */
float* pFloat=(float*)# /* pFloat represents the memory address of num, but set as a float */
printf("num's value is: %d\n",num); /* Display num's integer value */
printf("*pFloat's value is: %f\n",*pFloat); /* Display num's float value */
*pFloat=9.0; /* Change num's value to a float */
printf("num's value is: %d\n",num); /* Display num's integer value */
printf("*pFloat's value is: %f\n",*pFloat); /* Display num's float value */
}
The running result is as follows:
num's value is: 9
*pFloat's value is: 0.000000
num's value is: 1091567616
*pFloat's value is: 9.000000
It is completely unclear why there is such a large difference between the floating-point and integer results. To understand this result, one must grasp how floating-point numbers are represented internally in the computer.
>>>>
Floating-Point Encoding Method
1. IEEE Encoding for float Type
The float type occupies 4 bytes (32 bits) in memory. The highest 1 bit is used for the sign, 8 bits for the exponent, and the remaining bits for the mantissa (significant digits), as shown in the figure.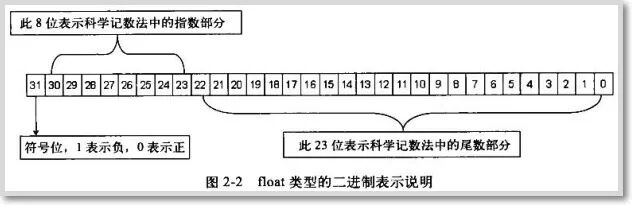
To convert a single-precision floating-point number to the IEEE standard encoding, scientific notation is used. For example, to store 12.25f in memory, it must first be converted to the corresponding binary number 1100.01.Using scientific notation, it is represented as 1.10001 << 3, meaning the decimal point is shifted 3 places to the right to the highest bit of 1, so the exponent is 3, the sign is 0 (positive), and the value is 110001. The formula can be summarized as:V = (-1)*S*(M<<E)where V is the floating-point number, S is the sign (0 or 1), M is the mantissa, and E is the exponent. In scientific notation, E can be negative, so E cannot be directly stored in the computer.E is represented using an 8-bit binary number, which can represent a range of 0~255. To accommodate negative values, IEEE 754 specifies that the midpoint value of 127 is treated as zero, meaning 0~126 represents negative values, and 127~255 represents non-negative values. Thus, for 12.25f, the exponent is 3, and when stored in the computer, it is offset by 3 from the zero point of 127, resulting in 127+3=130, which converts to binary as 1000 0010. When the exponent is extracted, it is reversed to obtain 3. Moreover, the integer part of the mantissa M is always 1, so only the fractional part is kept to save one significant digit.In a 32-bit floating-point number, 23 bits represent M, meaning that after omitting the first 1, it can save 24 significant digits. In summary, the binary storage for 12.25f is: 0 10000010 10001000000000000000000
- Sign bit: 0
- Exponent: 1000 0010
- Mantissa: 1000 1000 0000 0000 0000 000, converting to hexadecimal gives 0x41440000, which is stored in memory in little-endian format as 00 00 44 41.
It is not difficult to see that E has three cases: (1) E is neither all 0s nor all 1s. This is a normal representation, and the floating-point number is represented using the above rules, meaning the computed value of the exponent E is subtracted by 127 (range: -126~127) to obtain the true value. The mantissa M must have a leading 1, but this case ensures that M is a fraction between 1 and 2, and to reach 0, one must consider the second case.(2) E is all 0s. This is a non-normal representation, where M is a fraction between 0 and 1, and the true exponent E is 1-127=-126. The extra 1 is to compensate for the leading 1 removed from the mantissa, resulting in a mantissa of 0.xxxxxx. This case is used to represent ±0.0 and very small numbers close to 0.0.(3) E is all 1s. This is a special value; if the mantissa M is all 0s, it represents ±infinity (positive or negative depending on the sign bit); if the mantissa M is not all 0s, it represents NaN (Not a Number).
2. IEEE Encoding for double Type
The conversion process for double is the same as for float, but with increased precision, as shown in the figure:
In double, the highest 1 bit represents the sign bit, followed by 11 bits for the exponent, and the remaining 52 bits for the mantissa.For the conversion of double, just follow the same process!>>>>
Basic Floating-Point Instructions
As mentioned earlier, floating-point numbers use separate floating-point registers in the computer and do not occupy general-purpose registers. Therefore, operations on floating-point numbers actually involve a new set of instructions. Common floating-point instructions are as follows, where IN indicates operand push and OUT indicates operand pop: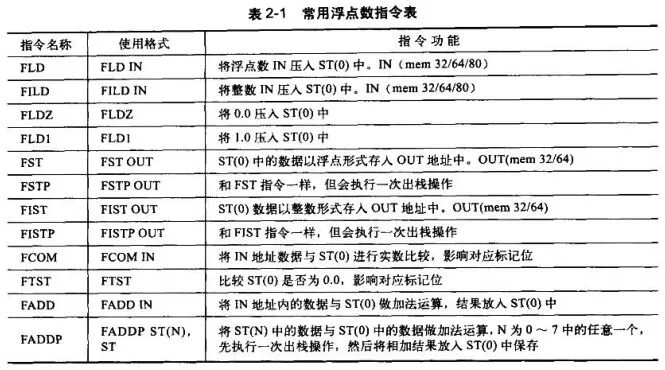
It can be observed that floating-point instructions all start with F, and there are also some similar to integer instructions, simply prefixed with F, such as: FSUB, FSUBP, etc. Floating-point registers are implemented through 8 stack spaces, represented as ST(0)-ST(7). Each floating-point register occupies 8 bytes, with the top of the stack being ST(0). When pushing onto the stack, the data in ST(0) moves towards ST(7), and when the registers are full, ST(7) data will be discarded. The following code is used to familiarize oneself with the usage of floating-point instructions. In VC++6.0, optimization compilation is disabled, and the following example converts int to float:
#include <stdio.h>
void main(int argc){
float fFloat = (float)argc;
printf("%f\n", fFloat);
}
The resulting assembly code is as follows:
00410940 push ebp
00410941 mov ebp,esp
00410943 push ecx
00410944 fild dword ptr ss:[ebp+0x8] ; Convert the integer at ebp+8 to float and push onto the floating-point register, corresponding to variable argc
00410947 fst dword ptr ss:[ebp-0x4] ; Extract the float and store it in ebp-4, corresponding to variable fFloat
0041094A sub esp,0x8 ; Allocate a double space at the top of the stack
0041094D fstp qword ptr ss:[esp] ; Float passed to variable argument function must first be converted to double, stored in esp in floating-point encoding
00410950 push ReverseT.00418E74 ; "%d\n"
00410955 call ReverseT.00401040 ; printf("%d\n", a)
0041095A add esp,0xC ; __cdelc convention, caller balances the stack
0041095D mov esp,ebp
0041095F pop ebp
00410960 retn
Although float occupies 4 bytes, it can be seen that it is processed as 8 bytes. Moreover, when float is used as a parameter in a variable argument function, it must be converted to double, as in the printf() function above. The following code demonstrates using __ftol to convert float to int, as shown below:
void main(int argc){
float fFloat = (float)argc;
printf("%f\n", fFloat);
argc = (int)fFloat;
printf("%d\n", argc);
}
The assembly code is as follows:
;;; Omitted code as above ;;;;
0041095D fld dword ptr ss:[ebp-0x4] ; Load the data at ebp-4 into the floating-point register, corresponding to variable fFloat
00410960 call ReverseT.00410910 ; Call __ftol
00410965 mov dword ptr ss:[ebp+0x8],eax ; Store the converted result in ebp+8, corresponding to variable argc
00410968 mov eax,dword ptr ss:[ebp+0x8] ; Below is the call to printf
0041096B push eax
0041096C push ReverseT.00418E78
00410971 call ReverseT.00401040
00410976 add esp,0x8
When floating-point numbers are used as parameters, they cannot be pushed onto the stack because the push instruction can only pass 4 bytes to the stack, while floating-point numbers are processed as 8 bytes, which would result in the loss of 4 bytes.Thus, it can be seen that generally, stack space is allocated using sub, and the data is placed onto the stack using the fstp instruction. In the above code, converting int to float is straightforward; simply push the integer onto the floating-point register and extract it. However, converting float to int requires handling with the __ftol function due to the 4-byte difference between floating-point and general-purpose registers. When using printf to output a floating-point number as an integer, the result is completely incorrect because printf interprets the corresponding parameter as 4-byte data in two’s complement form, which not only results in incorrect encoding but also loses 4 bytes of data. When outputting as a floating-point number, the corresponding parameter is treated as 8-byte data and interpreted in floating-point encoding. The same applies to floating-point numbers as return values; the data must first be placed in the floating-point register, and after the function call, it is extracted from the floating-point register. Example code is as follows:
#include <stdio.h>
float GetFloat()
{
return 12.05f;
}
void main(int argc){
float fFloat = GetFloat();
printf("%f\n", fFloat);
}
The assembly code is as follows:
0040101B push ebp
0040101C mov ebp,esp
0040101E push ecx
0040101F call ReverseT.0040100A ; Call GetFloat
;;;;;;;;;;;;;;;call 0040100A;;;;;;;;;;;;;;;;
00401010 push ebp
00401011 mov ebp,esp
00401013 fld dword ptr ds:[0x416344] ; Load the float into the floating-point register
00401019 pop ebp
0040101A retn
;;;;;;;;;;;;;;;end 0040100A;;;;;;;;;;;;;;;;;
00401024 fst dword ptr ss:[ebp-0x4] ; Extract data from the floating-point register into ebp-4, corresponding to variable fFloat
00401027 sub esp,0x8 ; Call printf
0040102A fstp qword ptr ss:[esp]
0040102D push ReverseT.00418A30 ; "%f\n"
00401032 call ReverseT.00401040
00401037 add esp,0xC
0040103A mov esp,ebp
0040103C pop ebp
0040103D retn
Characters and StringsStrings are sequences composed of multiple characters. In C++, a string is generally terminated with , meaning that reading up to 0 indicates the end of the string. The number of 0s and the space occupied by each character depend on the encoding method.>>>>
1. Character Encoding
Regarding encoding, the commonly used types can be roughly divided into two categories: ASCII and Unicode.ASCII can only represent 256 characters, using 1 byte for representation. Unicode encoding is universally applicable, allowing for a broader range of characters, with 65536 characters, using 2 bytes, where the first 256 characters are compatible with ASCII. For example, the character ‘a’ is represented in ASCII as 0x61 and in Unicode as 0x0061. Here is an ASCII code reference table downloaded from the internet: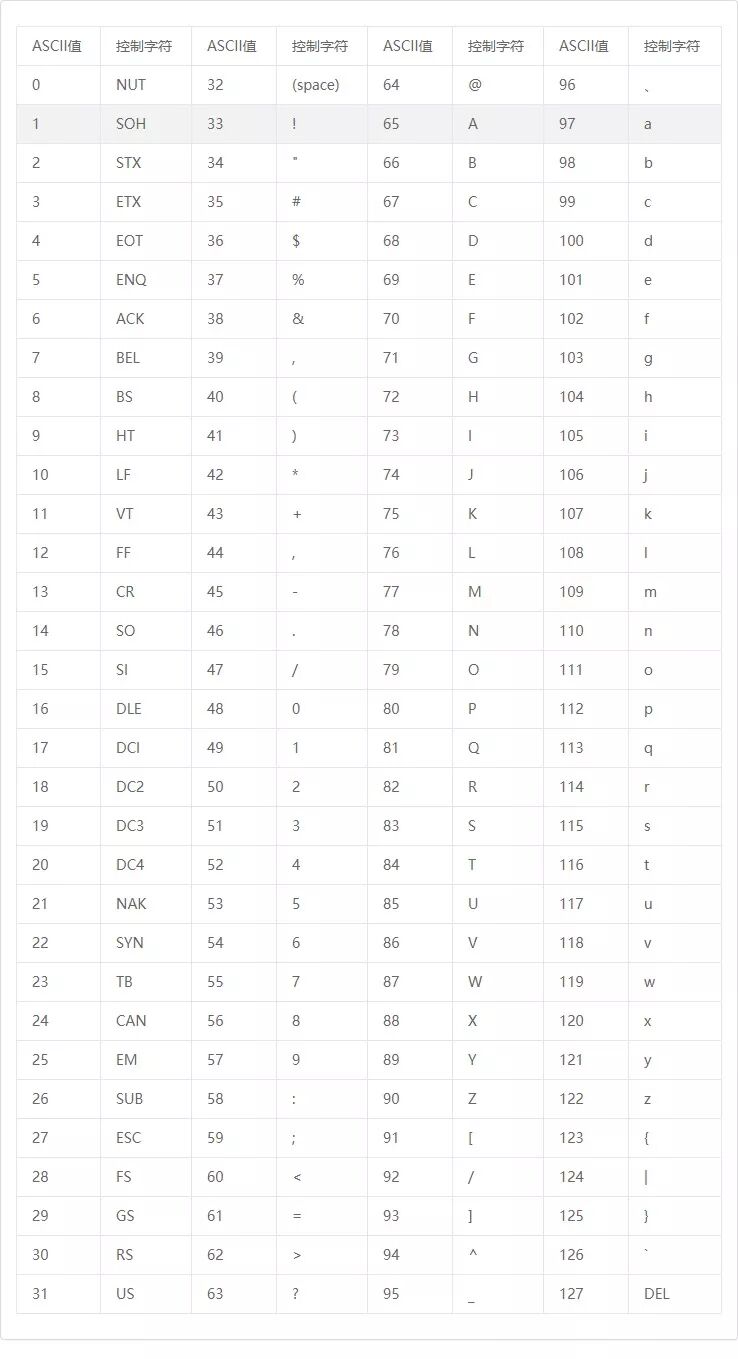
From the table, it can be seen that ASCII does not represent Chinese characters. However, in VC++ 6.0, attempting to printf, the code is as follows:
char* s = "汉子文化";
printf("%s\n", s);
According to that table, the result should be ?????, but it appears as follows:
汉子文化
Press any key to continue
It looks very normal; this is because the char in the program cannot actually store Chinese characters. The normal display occurs because the printf function hands the string over to the system for processing. Here, the cmd console uses GBK encoding, so it can parse the Chinese characters.Changing the program to store a Chinese character in a char results in the following code:
char s = '汉';
printf("%c\n",s);
The print result is as follows:
?
Press any key to continue
This shows that using char to store Chinese characters is incorrect. In C++ Windows development, char is used to define ASCII-encoded characters, while wchar_t is used to store Unicode-encoded characters.>>>>
2. String Storage Methods
Strings are stored sequentially in memory. When a string is defined, the variable stores the address of the first character. To determine the size of a string, both the starting and ending addresses must be known. There are two ways to determine the ending address: one is to store the string length in n bytes before the string, and the other is to set a special character at the end of the string to represent the end, i.e., the terminator. Each method has its pros and cons.> Saving Total LengthExchanging space for time.This method is common in communication protocols, such as the SOCKS protocol, which uses this method to transmit domain name information.> TerminatorExchanging time for space.In program development, this method is still common. For example, in C++, the terminator is used.For string content storage, ASCII encoding stores each character in one byte, while Unicode encoding stores each character in two bytes. Unicode characters are also known as wide characters, so in Windows development, functions that start with ‘w’ are usually designed for wide characters, such as: wprintf, wsprintf, etc. Through the VC++6.0 debugger, the differences in memory storage between char and wchar_t characters can be observed:
#include <cstdio>
#include <cwchar>
int main(void)
{
char* pcChar = "string!";
wchar_t* pwChar = L"wide string!";
return 0;
}
Memory storage for the two types of strings: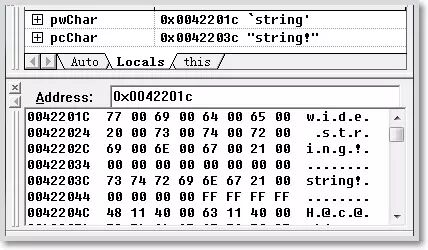
Here, pcChar starts at address 0042201Ch, with each byte representing 1 character, pwChar starts at address 0042203Ch, with each two bytes representing 1 character. If you want to output wide characters in VC++6.0, you should use the setlocale function to set the locale information, which should match the current system configuration. This can be checked in the CMD properties window. Example code is as follows:
#include <cstdio>
#include <cwchar>
#include <clocale>
int main()
{
setlocale(LC_ALL, ".936");
wchar_t c = L'汉';
wprintf(L"%lc\n", c);
return 0;
}
Boolean TypeIt is simply 0 and 1, where 0 represents false and non-0 represents true. The boolean type in C++ occupies 1 byte, and its storage method is the same as that of integers, which can be replaced by char, int, byte, etc.Addresses, Pointers, and ReferencesAddress:Generally, the address specifically refers to the logical memory address, with addressing methods referencing assembly register knowledge. In C++, addresses are commonly represented in hexadecimal. To obtain the address of a variable, the address-of operator & is used. Only variables can have their addresses taken; constants (including those specified by const or immediate values) cannot have their addresses taken.Pointer:A pointer is defined using “TYPE *”, where TYPE is the data type.A pointer is also a data type, and its size is not determined by the TYPE type but is fixed.A pointer variable only stores the address of a variable. When defining a pointer, the type name must be included to allow for appropriate interpretation of the data stored at the address.Each array variable name points to the address of the first element of the array, so the array name is also a pointer type.Reference:& Besides being able to take addresses, it can also create a reference for a variable, i.e., an alias. The definition method is similar to pointers:TYPE &, where TYPE is the data type.A reference must be initialized at the time of definition and cannot be defined alone.>>>>
Relationship Between Addresses and Pointers
Addresses are used to indicate memory numbers, i.e., the position of a variable in memory, while pointers are variables used to store addresses. >>>>
Pointer Addition and Subtraction
The only operators supported by pointers are addition and subtraction. Pointers exist to store data addresses and interpret addresses; other operators are not useful. Pointer addition is used for address offset. When a pointer is incremented by 1, it does not mean that the address stored in the pointer increases by 1, but rather that the address is increased based on the size of the type. The following code demonstrates this using pointers:
#include <stdio.h>
int main()
{
int array[] = {1,2,3,4,5};
int * piArray = array;
int i = 0;
for(i = 0; i < 5; i++)
{
printf("%d\n", *piArray);
piArray += 1;
}
return 0;
}
In VC++6.0, when the optimization compilation option “Maximize speed” is enabled, the compilation result is as follows:
00401010 sub esp,0x14 ; Allocate array space
00401013 push esi
00401014 push edi
00401015 mov edi,0x5 ; Corresponding variable i, here is a decrement loop
0040101A mov dword ptr ss:[esp+0x8],0x1 ; Create an array on the stack
00401022 mov dword ptr ss:[esp+0xC],0x2
0040102A mov dword ptr ss:[esp+0x10],0x3
00401032 mov dword ptr ss:[esp+0x14],0x4
0040103A mov dword ptr ss:[esp+0x18],edi
0040103E lea esi,dword ptr ss:[esp+0x8] ; Let esi point to the array, corresponding to variable piArray
00401042 mov eax,dword ptr ds:[esi] ; Call printf to output
00401044 push eax
00401045 push ReverseT.00414A30
0040104A call ReverseT.00401080
0040104F add esp,0x8
00401052 add esi,0x4 ; Increase based on pointer type size, not just add 1
00401055 dec edi
00401056 jnz short ReverseT.00401042
00401058 pop edi
00401059 xor eax,eax
0040105B pop esi
0040105C add esp,0x14
0040105F retn
From the above, it can be seen that pointer addition is related to the type, so adding two pointers is also meaningless.>>>>
References
Some say that references were invented as another access method after pointers. References are implemented based on pointers, simplifying pointer operations. This can be demonstrated with a piece of code:
#include <stdio.h>
int main()
{
int iVar;
scanf("%d", &iVar);
printf("%d", iVar);
return 0;
}
In VC++6.0, when the optimization compilation option "Maximize speed" is enabled, the compilation result is as follows:00401010 push ecx
00401011 lea eax,dword ptr ss:[esp] ; Pointer to iVar
00401015 push eax
00401016 push ReverseT.00414A30
0040101B call ReverseT.0040F890 ; Call scanf
00401020 mov ecx,dword ptr ss:[esp+0x8]
00401024 add esp,0x8
00401027 push ecx
00401028 push ReverseT.00414A30
0040102D call ReverseT.00401080 ; Call printf
00401032 xor eax,eax
00401034 add esp,0xC
00401037 retn
From this, it can be seen that both references and pointers use the lea instruction, so they are essentially the same thing.ConstantsConstants exist before the program runs and are directly compiled into the executable file. Once the program starts, they are loaded into memory.These data are usually stored in the constant data area (iData segment), which has no write permissions, so modifying constants will trigger program exceptions.
– End –
Kanxue ID:techliu
https://bbs.pediy.com/user-860174.htm
This article is original by Kanxue Forum techliu
Please indicate the source from Kanxue Community when reprinting
Popular reviews from previous issues
1. Basics of Cryptography: Base64 Encoding
2. Analyzing the Principle of InfinityHook, Sparking a More Intense Battle of Attack and Defense
3. [Android Modification Series] Analysis of Holographic Backup Principles
4. Writing Windows Kernel Shellcode
5. [Call for Speeches] Join Kanxue in Nanjing to See Security with “Trend Micro”!
﹀
﹀
﹀
Public Account ID: ikanxue
Official Weibo: Kanxue Security
Business Cooperation: [email protected]
↙Click on “Read the original text” below for more valuable content