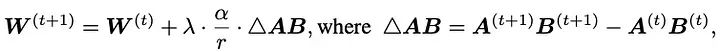Source: Deephub Imba
This article is about 4000 words long, and it is recommended to read in 6 minutes.
In this article, we will explain the basic concepts of LoRA itself and then introduce some variants that improve the functionality of LoRA in different ways.
LoRA can be said to be a major breakthrough for efficiently training large language models for specific tasks. It is widely applied in many applications. In this article, we will explain the basic concept of LoRA itself and then introduce some variants that improve the functionality of LoRA in different ways, including LoRA+, VeRA, LoRA-FA, LoRA-drop, AdaLoRA, DoRA, and Delta-LoRA.
LoRA
Low-Rank Adaptation (LoRA) is currently a widely used technique for training large language models (LLMs). Large language models can generate various content for us, but for solving many problems, we still hope to train LLMs on given downstream tasks, such as classifying sentences or generating answers to given questions. However, if fine-tuning is used directly, it requires training large models with millions to billions of parameters.
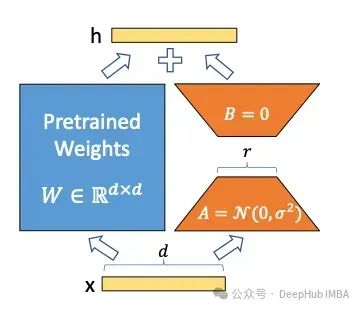
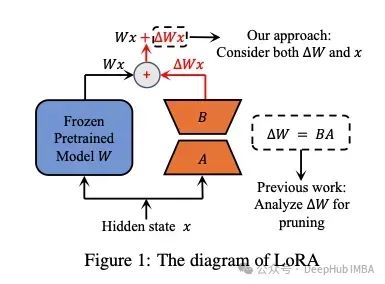
LoRA provides an alternative training method that reduces the number of parameters to be trained, making it faster and easier. LoRA introduces two matrices A and B; if the original parameter matrix W has a size of d × d, then matrices A and B have sizes of d × r and r × d, respectively, where r is much smaller (usually less than 100). The parameter r is called the rank. If LoRA is used with a rank of r=16, the shapes of these matrices are 16 x d, which greatly reduces the number of parameters that need to be trained. The main advantage of LoRA is that it requires fewer parameters to train compared to fine-tuning, yet achieves performance comparable to fine-tuning.
One technical detail of LoRA is that initially, matrix A is initialized with random values with a mean of zero, but with some variance around the mean. Matrix B is initialized as a completely zero matrix. This ensures that the LoRA matrices do not randomly alter the output of the original W from the start. Once the parameters of A and B are adjusted in the desired direction, the updates in A and B should complement the original output of W.
LoRA significantly reduces the resource consumption for training LLMs. Thus, many different variants have emerged based on the original LoRA method, each improving the original method in different ways.
LoRA+
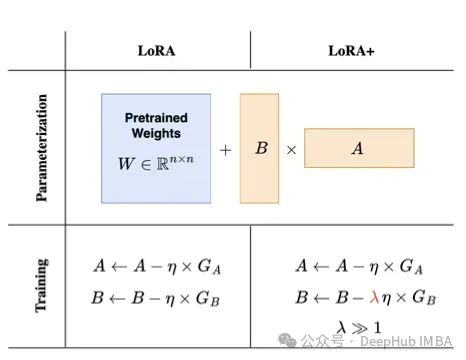
LoRA+ introduces a more effective method for training LoRA adapters by introducing different learning rates for matrices A and B. In standard LoRA, the learning rate is applied to all weight matrices during neural network training. The authors of LoRA+ have demonstrated that using a single learning rate is suboptimal. By setting the learning rate for matrix B to be much higher than that of matrix A, training efficiency can be improved.
The authors prove that the required mathematics is quite complex (if you’re really interested, you can check out the original paper). Let’s provide a simple explanation: matrix B is initialized to 0, so it requires larger update steps than the randomly initialized matrix A. By setting the learning rate for matrix B to be 16 times that of matrix A, the authors have been able to achieve a slight increase in model accuracy (about 2%) while doubling the training time for models like RoBERTa or Llama-7b.
VeRA
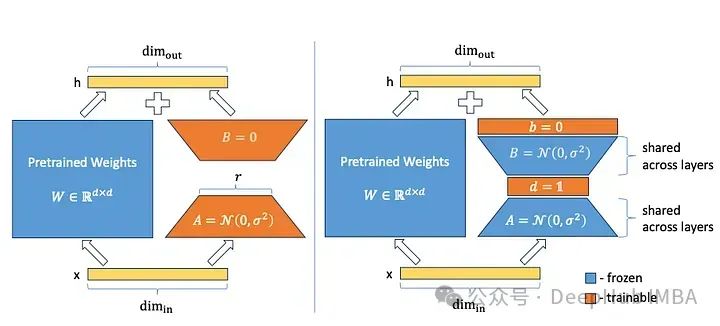
VeRA (Vector-based Random Matrix Adaptation) introduces a method to significantly reduce the size of LoRA parameters. They do not train matrices A and B but instead initialize these matrices with shared random weights (i.e., all matrices A and B across all layers have the same weights) and add two new vectors d and B, training only vectors d and B during fine-tuning.
A and B are random weight matrices. If they are not trained at all, how can they contribute to the model’s performance? This method is based on an interesting research area known as random prediction. Quite a bit of research indicates that in a large neural network, only a small portion of weights are used to guide behavior and lead to the expected performance of the model on training tasks. Thus, due to random initialization, certain parts (or sub-networks) of the model are more inclined to the desired model behavior from the start.
However, this means that all parameters need to be trained during the training process, which is no different from full fine-tuning. The authors of VeRA, by introducing vectors d and b, only train these relevant sub-networks, in contrast to the original LoRA method where matrices A and B are frozen, and matrix B is no longer set to zero but is randomly initialized like matrix A.
This method results in many parameters that are much smaller than the full matrices A and B. If a LoRA layer with a rank of 16 is introduced into GPT-3, it would have 755,000 parameters. Using VeRA, only 28 million parameters are needed (a reduction of 97%). How does performance hold up with so few parameters? The authors of VeRA evaluated using common benchmarks like GLUE or E2E, as well as models based on RoBERTa and GPT-2 Medium. The results indicate that the performance of the VeRA model is only slightly lower than that of fully fine-tuned models or those using the original LoRA technique.
LoRA-FA
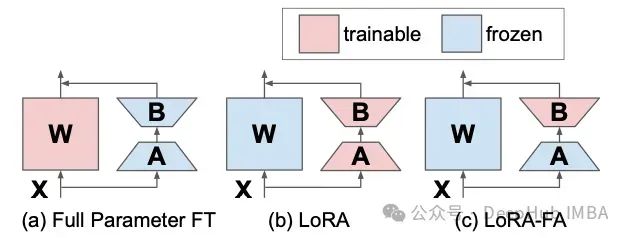
LoRA-FA, which stands for LoRA with Frozen-A, freezes matrix A after initialization, serving as a random projection. Matrix B is not adding new vectors but is trained after being initialized to zero (just like in the original LoRA). This halves the number of parameters while maintaining performance comparable to standard LoRA.
LoRA-drop
The LoRA matrix can be added to any layer of the neural network. LoRA-drop introduces an algorithm to determine which layers are fine-tuned with LoRA and which do not need it.
LoRA-drop consists of two steps. In the first step, a subset of the data is sampled, and LoRA is trained for several iterations. Then, the importance of each LoRA adapter is calculated as BAx, where A and B are the LoRA matrices, and x is the input. This is the output of LoRA added to the output of the frozen layer. If this output is large, it indicates that it will significantly change behavior. If it is small, it indicates that the impact of LoRA on the frozen layer is minimal and can be ignored.
There are also different methods for selecting the most important LoRA layers: importance values can be summed until a threshold is reached (controlled by a hyperparameter), or only the most important n fixed LoRA layers can be taken. Regardless of the method used, a full training on the entire dataset is still required (since a subset of data was used in previous steps), with other layers fixed to a set of shared parameters that will not change during training.
The LoRA-drop algorithm allows for training a model using only a subset of LoRA layers. According to the evidence presented by the authors, there is only a slight change in accuracy compared to training all LoRA layers, but due to the fewer parameters that need to be trained, computational time is reduced.
AdaLoRA
There are many ways to determine which LoRA parameters are more important than others, and AdaLoRA is one of them. The authors of AdaLoRA suggest considering the singular values of the LoRA matrices as indicators of their importance.
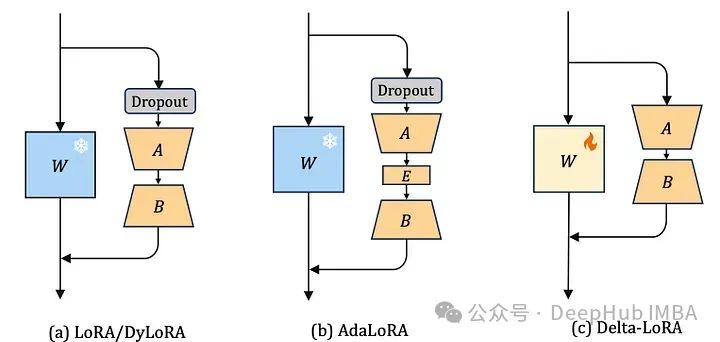
In contrast to the above LoRA-drop, where the layer’s adapters are either fully trained or not trained at all, AdaLoRA can determine that different adapters have different ranks (in the original LoRA method, all adapters have the same rank).
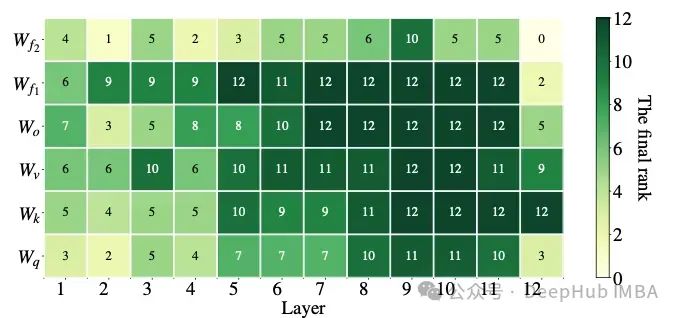
AdaLoRA has the same total number of parameters as standard LoRA with the same rank, but the distribution of these parameters is different. In LoRA, all matrices have the same rank, while in AdaLoRA, some matrices have higher ranks and others have lower ranks, so the total number of parameters remains the same. Experiments show that AdaLoRA produces better results than the standard LoRA method, indicating better distribution of trainable parameters in parts of the model, which is particularly important for given tasks. The following figure illustrates how AdaLoRA ranks layers for a given model. As we can see, it provides higher ranks to layers closer to the end of the model, indicating that adapting these is more important.
DoRA
Another method to modify LoRA for better performance is Weight-Decomposed Low-Rank Adaptation (DoRA). Since every matrix can be decomposed into a product of size and direction. For vectors in two-dimensional space, it can be easily imagined: a vector is an arrow starting from the position 0 and ending at a point in vector space. For the elements of the vector, if your space has two dimensions x and y, you can say x=1 and y=1. Or you can describe the same point in a different way by specifying size and angle (i.e., direction), such as m=√2 and a=45°. This means moving the arrow from point 0 along a 45° direction a length of √2. You would end up with the same point (x=1, y=1).
This size and direction decomposition can also be accomplished with higher-order matrices. The authors of DoRA apply this to the weight matrix, which describes the updates in the training steps of models trained using standard fine-tuning and those trained using LoRA adapters. The comparison of these two techniques can be seen in the figure below:
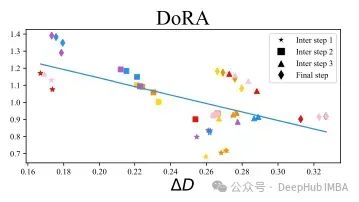
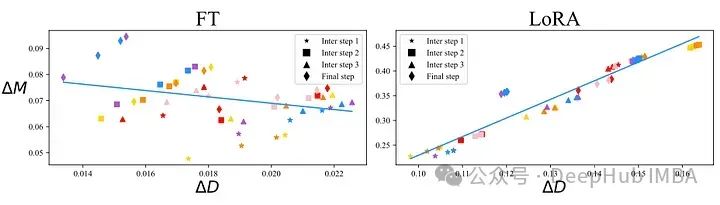 Fine-tuned model (left) and model trained using LoRA adapters (right). On the x-axis, you can see the changes in direction, and on the y-axis, you can see the changes in magnitude, with each scatter point belonging to a layer of the model. There is a significant difference between these two training methods. In the left figure, there is a small negative correlation between direction updates and magnitude updates, while in the right figure, there is a stronger positive correlation. You might wonder which is better or if this has any significance. However, the main idea of LoRA is to achieve performance equivalent to fine-tuning while using fewer parameters. In other words, as long as costs are not increased, LoRA training can share as many attributes as possible. The figure above also shows that the relationship between direction and magnitude in LoRA differs from that in full fine-tuning, which may be one reason why LoRA sometimes underperforms compared to fine-tuning.
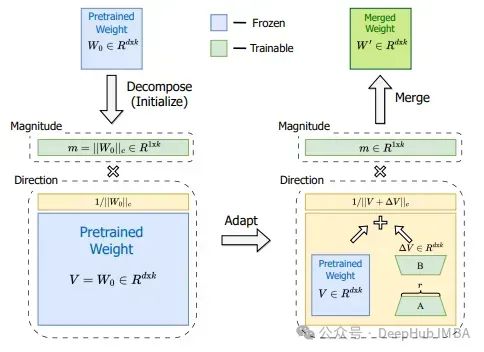
The authors of DoRA introduce a method to separate the pre-trained matrix W into a size 1 x d vector m and a direction matrix V, allowing for independent training of size and direction. The direction matrix V is enhanced by B * a, while m is trained as is. While LoRA tends to change both magnitude and direction simultaneously (as indicated by the high positive correlation between the two), DoRA can more easily separate the two adjustments or compensate for one change with a negative change in the other. Thus, the relationship between direction and magnitude in DoRA is more like that of fine-tuning:
In several benchmark tests, DoRA outperformed LoRA in terms of accuracy. Decomposing weight updates into size and direction allows DoRA to perform training closer to what is done in fine-tuning while still using the smaller parameter space of LoRA.
Fine-tuned model (left) and model trained using LoRA adapters (right). On the x-axis, you can see the changes in direction, and on the y-axis, you can see the changes in magnitude, with each scatter point belonging to a layer of the model. There is a significant difference between these two training methods. In the left figure, there is a small negative correlation between direction updates and magnitude updates, while in the right figure, there is a stronger positive correlation. You might wonder which is better or if this has any significance. However, the main idea of LoRA is to achieve performance equivalent to fine-tuning while using fewer parameters. In other words, as long as costs are not increased, LoRA training can share as many attributes as possible. The figure above also shows that the relationship between direction and magnitude in LoRA differs from that in full fine-tuning, which may be one reason why LoRA sometimes underperforms compared to fine-tuning.
The authors of DoRA introduce a method to separate the pre-trained matrix W into a size 1 x d vector m and a direction matrix V, allowing for independent training of size and direction. The direction matrix V is enhanced by B * a, while m is trained as is. While LoRA tends to change both magnitude and direction simultaneously (as indicated by the high positive correlation between the two), DoRA can more easily separate the two adjustments or compensate for one change with a negative change in the other. Thus, the relationship between direction and magnitude in DoRA is more like that of fine-tuning:
In several benchmark tests, DoRA outperformed LoRA in terms of accuracy. Decomposing weight updates into size and direction allows DoRA to perform training closer to what is done in fine-tuning while still using the smaller parameter space of LoRA.
Delta-LoRA
Delta-LoRA introduces another idea to improve LoRA by allowing the pre-trained matrix W to play a role again. The main idea of LoRA is not to adjust the pre-trained matrix W because it is resource-intensive. LoRA introduces new smaller matrices A and B that learn downstream tasks less effectively, so the performance of models trained with LoRA is usually lower than that of fine-tuned models.
The authors of Delta-LoRA propose to update matrix W using the gradient of AB, where the gradient of AB is the difference between A*B at two consecutive time steps. This gradient is scaled by a hyperparameter λ, which controls how much influence the new training should have on the pre-trained weights.
This introduces more parameters that need to be trained with almost no computational overhead. It does not require calculating the gradient of the entire matrix W as in fine-tuning, but instead uses the gradients already obtained during LoRA training to update it. The authors compared this method using models like RoBERTA and GPT-2 across many benchmark tests and found that this method shows improved performance compared to the standard LoRA approach.
Summary
The research area of LoRA and its related methods is very active, with new contributions emerging daily. This article explains the core ideas of some methods. If you are interested in these methods, please check the papers:
[1] LoRA: Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). LoRA: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
[2] LoRA+: Hayou, S., Ghosh, N., & Yu, B. (2024). LoRA+: Efficient Low Rank Adaptation of Large Models. arXiv preprint arXiv:2402.12354.
[3] VeRA: Kopiczko, D. J., Blankevoort, T., & Asano, Y. M. (2023). VeRA: Vector-based random matrix adaptation. arXiv preprint arXiv:2310.11454.
[4]: LoRA-FA: Zhang, L., Zhang, L., Shi, S., Chu, X., & Li, B. (2023). LoRA-FA: Memory-efficient low-rank adaptation for large language models fine-tuning. arXiv preprint arXiv:2308.03303.
[5] LoRA-drop: Zhou, H., Lu, X., Xu, W., Zhu, C., & Zhao, T. (2024). LoRA-drop: Efficient LoRA Parameter Pruning based on Output Evaluation. arXiv preprint arXiv:2402.07721.
[6] AdaLoRA: Zhang, Q., Chen, M., Bukharin, A., He, P., Cheng, Y., Chen, W., & Zhao, T. (2023). Adaptive budget allocation for parameter-efficient fine-tuning. arXiv preprint arXiv:2303.10512.
[7] DoRA: Liu, S. Y., Wang, C. Y., Yin, H., Molchanov, P., Wang, Y. C. F., Cheng, K. T., & Chen, M. H. (2024). DoRA: Weight-Decomposed Low-Rank Adaptation. arXiv preprint arXiv:2402.09353.
[8]: Delta-LoRA: Zi, B., Qi, X., Wang, L., Wang, J., Wong, K. F., & Zhang, L. (2023). Delta-LoRA: Fine-tuning high-rank parameters with the delta of low-rank matrices. arXiv preprint arXiv:2309.02411.
Editor: Wang Jing