Recently, I encountered a problem with byte endian conversion in a protocol, so I lazily went online to check it out and came across a similar issue, learning a new term called butterfly swapping.
The Problem Is As Follows
The protocol requires that the low byte is on the left and the high byte is on the right, and each byte needs to be converted by swapping its high and low bits. For example,<span>11010001</span>, after swapping bits according to<span>0->7, 1->6, 2->5, 3->4</span>, it becomes<span>10001011</span>.
Here, knowledge of bit manipulation is required. Let’s take an 8-bit data endian conversion as an example:
#include <stdio.h>
unsigned char highAndLowShiftHEX(unsigned char data);
void printBin(int n);
int main () {
highAndLowShiftHEX(209);
return 0;
}
unsigned char highAndLowShiftHEX(unsigned char data)
{
unsigned char i;
unsigned char tmp=0x00;
for(i=0;i<8;i++)
{
tmp=((data>>i)&0x01)|tmp;
//printBin(tmp);
if(i<7)
tmp=tmp<<1;
}
printf("\nafter shift data:");
printBin(tmp);
return tmp;
}
// Since binary is intuitive, I wrote a function to print binary
void printBin(int n) {
int len = sizeof(n)*8; // total bits.
int i;
if(i == 0) {
printf("0");
return;
}
for(i = len-1; i >= 0; i --) // skip leading 0s.
{
if(n&(1<<i)) break;
}
for(;i>=0; i --)
printf("%d", (n&(1<<i)) != 0);
}
If you are familiar with bit manipulation, the above code is relatively simple to implement. In embedded development, this kind of problem is usually solved using the butterfly swapping method and lookup table method.
Higher Level Implementation?
-
Assuming the original sequence is: 1 2 3 4 5 6 7 8 -
The target sequence is: 8 7 6 5 4 3 2 1
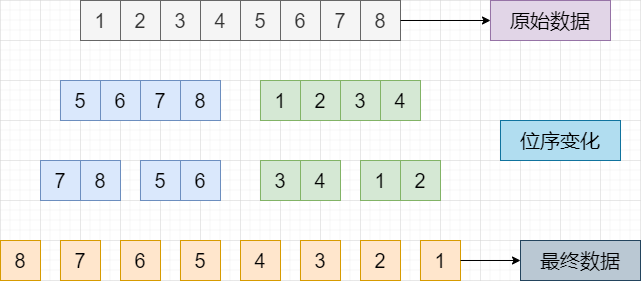
This completes the entire bitwise reverse conversion. Similarly, taking<span>11010001</span> as an example, here is the specific implementation code:
#include <stdio.h>
unsigned char highAndLowShiftHEX(unsigned char );
void printBin(int );
int main () {
highAndLowShiftHEX(209);
return 0;
}
unsigned char highAndLowShiftHEX(unsigned char data)
{
data=(data<<4)|(data>>4);
data=((data<<2)&0xcc)|((data>>2)&0x33);
data=((data<<1)&0xaa)|((data>>1)&0x55);
printf(" after shift data=%x \n",data);
printBin(data);
return data;
}
// Since binary is intuitive, I wrote a function to print binary
void printBin(int n) {
int len = sizeof(n)*8; // total bits.
int i;
if(i == 0) {
printf("0");
return;
}
for(i = len-1; i >= 0; i --) // skip leading 0s.
{
if(n&(1<<i)) break;
}
for(;i>=0; i --)
printf("%d", (n&(1<<i)) != 0);
}
Exchanging the high and low bits of a byte is not a very common problem. When encountering this issue, careful analysis is required, along with a proficient grasp of bit manipulation in C language to effectively solve such problems.
Extension
Now we will extend this to high and low bit conversion of 16-bit half-word data.
The principle is the same as with 8 bits, using simple shifting methods to convert the high and low bits of the data. If you are familiar with bit manipulation, the code becomes relatively simple.
Below is the specific implementation of this idea.
#include <stdio.h>
void expandPrintBin(int val2);
unsigned short HighAndLowSwitchHEX(unsigned short data);
int main () {
HighAndLowSwitchHEX(38491);
return 0;
}
// Since binary is intuitive, I wrote an extended function to print binary
void expandPrintBin(int val2) {
int i,k;
unsigned char *p = (unsigned char*)&val2 + 3; // from low to high, low-end byte computer
for( k = 0; k <= 3; k++) {
int val2 = *(p-k);
for (i = 7; i >= 0; i--) {
if(val2 & (1 << i))
printf("1");
else
printf("0");
}
printf(" ");
}
}
unsigned short HighAndLowSwitchHEX(unsigned short data) {
unsigned char i = 0;
unsigned short temp = 0x0000;
for(i = 0; i < 16; i++) {
temp = ((data >> i) & 0x0001) | temp;
if(i < 15) {
temp = temp << 1;
}
}
printf("temp:%x\n\n",temp);
expandPrintBin(temp);
return temp;
}
-
Assuming the original sequence is: <span>a b c d e f g h i j k l m n o p</span> -
The target sequence is: <span>p o n m l k j i h g f e d c b a</span>
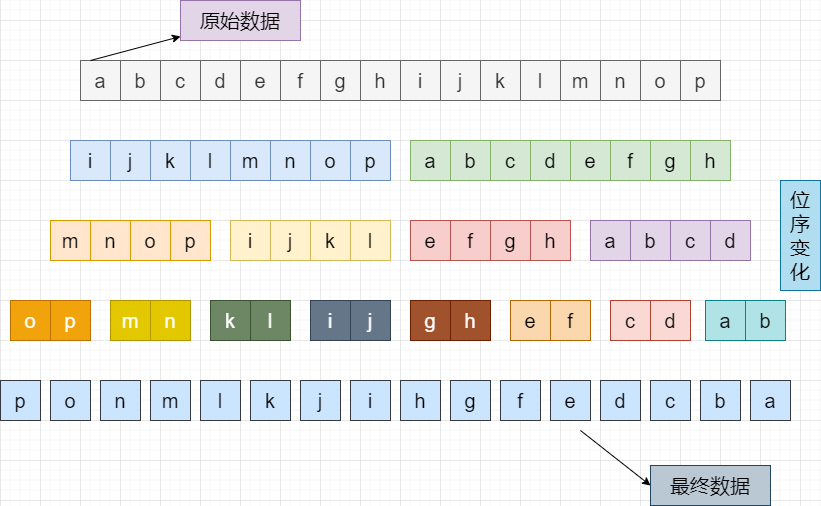
This completes the entire bitwise reverse conversion, completing the algorithm extension. Taking<span>1001011001011011</span> as an example, here is the specific implementation code:
#include <stdio.h>
unsigned short highAndLowShiftHEX(unsigned short data);
void expandPrintBin(int val2);
int main () {
highAndLowShiftHEX(38491);
return 0;
}
unsigned short highAndLowShiftHEX(unsigned short data) {
data = (data << 8) | (data >> 8); //0101101110010110
data = ((data << 4) & 0xF0FF) | ((data >> 4) & 0xFF0F); //1011010101101001
data = ((data << 2) & 0xCCCC) | ((data >> 2) & 0x3333); //1110010110010110
data = ((data << 1) & 0xAAAA) | ((data >>1 ) & 0x5555); //1101101001101001
printf(" after shift data=%x \n",data);
expandPrintBin(data);
return data;
}
// Since binary is intuitive, I wrote an extended function to print binary
void expandPrintBin(int val2) {
int i,k;
unsigned char *p = (unsigned char*)&val2 + 3; // from low to high, low-end byte computer
for( k = 0; k <= 3; k++) {
int val2 = *(p-k);
for (i = 7; i >= 0; i--) {
if(val2 & (1 << i))
printf("1");
else
printf("0");
}
printf(" ");
}
}
Conclusion
The key to the above problem is the flexible use of bit manipulation. Additionally, two functions for printing binary were written for convenience, and the code can be directly used. Debugging is not easy, so likes, views, and shares are appreciated. See you next time!
Author: Li Xiaoyao, Source: Technology Makes Dreams Greater
This article is reprinted with permission from the “Technology Makes Dreams Greater” public account. Reprinting is for learning reference only and does not represent this account’s agreement with its views. This account is not responsible for any infringement of its content, text, or images.