
Author:Tian Feng
“The Snow Walker” Full Text
Editor’s Note: “Industrial Software Cloud Strategy” is a monumental work edited by Qiu Shuiping, CTO of Huawei Industrial Software and Industrial Cloud, and Secretary-General of the Digital Industrial Software Alliance (DISA), co-authored by several experts from the DISA. This article is a chapter written by experts from Anshi Asia Pacific.

Chapter Index:
-
Chapter 4: Rooted: The Industrial Software Cloud Operating System, Enabling a New Generation of Industrial Software Ecosystem
-
Section 3: The Root of Tool Software: Kernel Engine Technology, Enabling Super Robust Industrial Software
-
Subsection 5: High-Performance Numerical Computing Engine
The high-performance numerical computing engine is the core computational module of industrial software, providing fundamental data structures such as matrices and vectors required by industrial software. It defines the underlying data and interfaces of industrial software, and through basic algorithms such as matrix-vector operations, solving linear equations, solving nonlinear equations, time discretization, optimization, and domain decomposition, it enables modeling and computational analysis in various simulation fields such as CAD/CAE software for structures, fluids, electromagnetics, and multiphysics coupling.
If industrial software is likened to a robot, then the high-performance numerical computing engine is its chip brain, responsible for numerical computation and analysis throughout the industrial software chain. With the continuous advancement of science and technology, most physical phenomena in the vast world can be described using mathematical and physical equations. Software like CAD/CAE designs and establishes geometric and physical models, obtaining computational data corresponding to mathematical and physical equations through different discretization methods. This data is read into the high-performance numerical computing engine through a unified interface for solution computation, yielding corresponding simulation results.
The high-performance numerical computing engine, as the chip brain of industrial software, directly determines the accuracy and computational efficiency of CAD/CAE software in simulation calculations across various fields such as structures, fluids, and electromagnetics. A single algorithm is merely a basic implementation for a specific problem and cannot meet the numerical computation needs of industrial software for different scenarios. It lacks unified adaptation and heterogeneous parallel architecture across platforms, failing to resolve issues of singular and ill-conditioned matrices that arise in complex models, and the stability, computational accuracy, and efficiency of the algorithms do not reach the level required for engineering applications.
The high-performance numerical computing engine started earlier abroad, with many mature commercial and open-source numerical computing engines already applied in engineering fields. In contrast, domestic numerical algorithms in this engine are primarily used for point-to-point research, and a systematically complete high-performance numerical computing engine that can support industrial software computation has yet to emerge.
Current Development Status of Domestic and Foreign Computing Engines
Mature industry simulation software abroad has unique advantages in the application of numerical algorithms and types of problems solved. Among them,ANSYS, ABAQUS, and COMSOL are representative large general-purpose software that exhibit good convergence and stability in core numerical algorithms.
ANSYS’s Sparse direct solution provides a direct method for solving sparse matrices, while iterative methods such as PCG, JCG, ICCG, and AMG solve large sparse matrices. The Newton-Raphson Method is used for solving nonlinear equations, and the Unsymmetric Method supports asymmetric solutions. The algorithms support shared memory and distributed parallelism.
ABAQUS features implicit, explicit, and parallel solvers, providing Direct Linear equation solver, Iterative Linear equation solver, and other direct algorithms, as well as incremental methods, direct iterative methods, Newton-Raphson methods, and Riks arc-length methods for nonlinear algorithms.
COMSOL integrates direct methods such as MUMPS, PARDISO, and SPOOLES, as well as iterative solvers like GMERS, FGMRES, BiCGSTAB, and CG, supporting various preconditioners such as ILU and SOR. It utilizes ARPACK for eigenvalue computation and Newton iteration methods for nonlinear problems.
Numerical simulation abroad started earlier, and with the continuous development of industrialization, many large research institutions have developed open-source libraries for numerical algorithms, such as BLAS, LAPACK, Intel MKL, SuperLU, MUMPS, PETSc, and Trilinos, which have been widely applied in both domestic and international research and engineering fields.
BLAS was first released in 1979, written in Fortran, and can perform basic linear algebra operations such as vector and matrix operations. It is the core of many numerical computing software libraries. The BLAS library is widely used in high-performance computing, leading to the derivation of many optimized versions, such as Intel MKL, AMD ACML, Goto BLAS, and ATLAS, as well as CUBLAS, which utilizes GPU computing technology.
LAPACK provides a function library for solving linear equations through matrix decompositions (LU, Cholesky, QR, SVD, Schur, etc.), least squares, eigenvalue problems, and singular value problems, handling dense and banded matrices. Intel MKL is a highly optimized and widely threaded mathematical library that provides C and Fortran interfaces, achieving good multithreading efficiency on Intel hardware.
Petsc and Trilinos are open-source projects from the U.S. Department of Energy, providing scalable (parallel) solutions for scientific applications of partial differential equation models, supporting MPI and GPU (CUDA & OpenCL) as well as hybrid MPI-GPU parallelism. They include numerous parallel linear and nonlinear solvers, ODE integration, Tao optimization, etc., and are widely used in fields such as structures, fluids, acoustics, and materials.
Domestic CAD/CAE software is increasingly industrialized, and simulation software has made significant progress in fields such as structures, fluids, and electromagnetics, with substantial improvements in computational accuracy and efficiency. The significant progress and development of domestic software in high-performance numerical computing are largely attributed to the superior computational performance and user-friendly nature of third-party open-source libraries. Domestic CAE software is still at the level of integrating open-source software and solving specific problem algorithms, without forming a complete high-performance numerical computing engine that supports simulation calculations across various disciplines, addressing issues such as solving large sparse matrices, matrix singularity and ill-conditioning, algorithm stability and convergence, and parallel computing and GPU acceleration.
Core Technologies of the Computing Engine
The high-performance numerical computing engine, as the computational core of industrial software, provides the underlying basic data structures and solution algorithm calls for simulation software like CAD/CAE. It needs to have a foundational framework supporting data and algorithm implementation, basic data structures and parallelism, system data I/O and unified interfaces, as well as core numerical algorithms including direct methods, iterative methods, preconditioning, ODE, eigenvalue solving, function interpolation, and nonlinearity. It is a complete and extensible scientific computing library for industrial software.
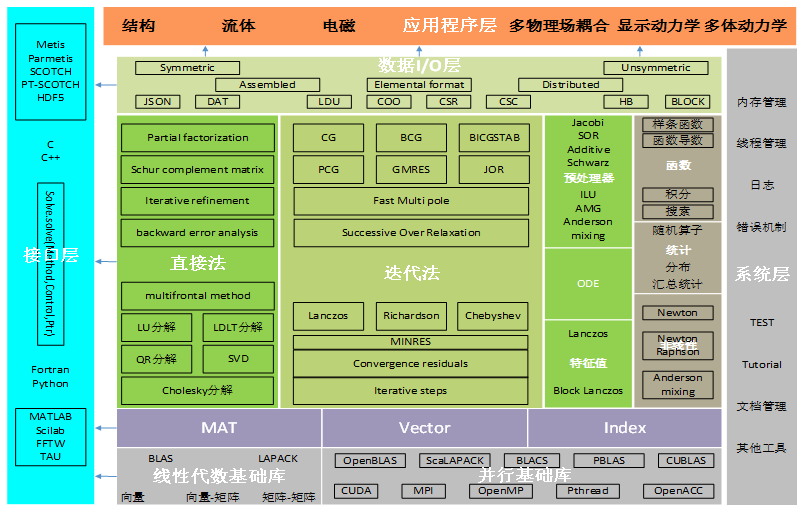
1) Linear Algebra Basic Module
The linear algebra basic library is a collection of common vector and matrix data structures and basic operation functions for linear algebra computations based on domestic hardware. The functions include linear operations on vectors, operations between matrices and vectors, and operations between matrices. The basic library defines the function interfaces and unified operation specifications, supporting data types such as single precision floating-point (S), double precision floating-point (D), complex (C), and 16-bit complex (Z). It can use formats such as dense matrices, banded matrices, symmetric matrices, symmetric banded matrices, compressed storage symmetric matrices, Hermitian matrices, banded Hermitian matrices, compressed storage Hermitian matrices, triangular matrices, triangular banded matrices, and compressed storage triangular matrices.
2) Parallel Computing Basic Module
The parallel basic library implements matrix partitioning, matrix rearrangement, matrix assembly, thread management, distributed communication, and heterogeneous parallelism for solving large-scale equation systems, providing a programming environment that supports OpenMP, thread, MPI, CUDA, OpenCL, and other shared memory, distributed memory, and heterogeneous parallelism.
3) Numerical Solution Algorithms
The intermediate layer of the high-performance numerical computing engine is the specific algorithm implementation for the computational analysis process of software like CAD/CAE, based on the underlying basic data structures, providing a unified interface for direct calls by industrial software.
(a) Direct Methods
Direct methods include Gaussian elimination, triangular decomposition, the Thomas algorithm, and multi-front methods, featuring LU decomposition, Cholesky decomposition, LDLT decomposition, QR decomposition, Schur decomposition, and SVD decomposition. They can directly solve symmetric, asymmetric, positive definite, non-positive definite, sparse, and dense matrices in industrial software simulation problems. Direct methods consume a large amount of memory and are less suitable for large-scale linear equation systems, where the applicability and computational efficiency of iterative methods far exceed those of direct methods.
(b) Iterative Methods and Preconditioning
Common iterative methods include CG, PCG, BICGSTAB, GMRES, FGMRES, and QMR. For ill-conditioned matrices generated by complex models, iterative solving methods combined with preconditioners (SSOR, ILU, GMG, AMG, etc.) preprocess the matrices, improving the convergence speed and computational efficiency of iterative solutions for ill-conditioned or large-scale coefficient matrices by reducing the condition number.
(c) Eigenvalue Solving
Eigenvalue solvers are applied in fields such as electromagnetics, mechanics, and structural vibrations, solving modal analysis problems by finding the corresponding eigenvalues and eigenvectors of equations. Common methods include QR decomposition, Lanczos method, and Block Lanczos method.
(d) Nonlinear Solving
Nonlinear solvers are based on Newton’s iteration method (linear search and trust region methods), relying on linear solvers to address nonlinear equations, materials, and contact issues in structures, fluids, and multiphysics coupling. They include Newton, Newton-Raphson, Anderson mixing, and other iterative methods, linear search methods, and iterations related to nonlinear calculations, such as step numbers, errors, and convergence.
Additionally, the intermediate algorithm layer provides region management, time integration, optimization, ODE, function interpolation, and statistical algorithms, enhancing the versatility of the high-performance numerical computing engine in industrial software.
Future Development Trends of the Computing Engine
With the continuous development of simulation technology and computer hardware, systems capable of trillions of calculations per second are emerging, and problems in the numerical computing field are trending towards high nonlinearity and large scale. High-performance computing is used to handle computationally intensive tasks in industrial software during simulation, modeling, computation, and rendering.
1) Shared Memory
Multi-threaded calculations on a single workstation through shared memory allow any computing core to access all memory via global addresses, leveraging the performance of multiple processors to accelerate industrial software computations. The shared memory method supports CPU-side programming models such as OpenMP, Pthread, and GPU-side models like OpenCL, CUDA, and OpenAcc.
2) Distributed Parallelism
Multi-node clusters are connected via inter-networking, working collaboratively to complete the same task, with each node accessing only local memory and storage. Information exchange between nodes and processing at each node occur in parallel. Through domain decomposition and node communication algorithms, large-scale matrix computations are transformed into multiple sub-tasks distributed to each node. Distributed parallelism supports MPI programming models and can solve E-level computational problems in numerical simulations.
The future of the high-performance numerical computing engine lies in achieving ultra-large-scale numerical simulation computations with high precision and efficiency based on continuously evolving supercomputer hardware, enabling industrial software to rapidly complete full-process simulations of entire vehicles and machines, rather than merely stopping at single-point simulations of sub-components and sub-structures. At the foundational algorithm level, it is necessary to improve the computational efficiency of matrix-vector multiplication adapted to domestic hardware environments, enhance optimization algorithms for solving large sparse matrices, and improve the computational stability of singular and ill-conditioned matrices. Furthermore, the ultra-large-scale computational capacity of high-performance numerical computing needs to reach E-level or even higher scales, based on national supercomputing centers such as Tianhe-1, Tianhe-2, Sunway TaihuLight, and Jinan Supercomputing, as well as domestic hardware ecosystems like Sugon and Huawei, to achieve GPU acceleration and heterogeneous parallelism under different parallel architecture systems.
Want a signed copy?Purchase this book from the Anshi Asia Pacific Mall. Any reader willing topost a photo and brief review of this book in their social circle can buy a signed copy from the author.



Author: Tian Feng
Deep thinker in industrial software, Director of the Beijing Comprehensive Simulation Engineering Laboratory, member of the National Industrial Foundation Committee, member of the Chinese Society of Mechanics, and member of the Chinese Mechanical Engineering Society. He has led the development of large industrial software such as lean R&D platforms, knowledge engineering platforms, comprehensive simulation platforms, knowledge cloud platforms, and simulation tools, which have been applied in major national industrial sectors such as aerospace, shipping, nuclear energy, petrochemicals, and vehicles; he has presided over more than 20 special projects related to the National Development and Reform Commission, the Ministry of Science and Technology, Beijing’s industrial foundation strengthening project, and industrial internet, providing consulting on lean R&D, knowledge engineering, and comprehensive simulation for over a hundred enterprises.
This book introduces the current status and development trends of the Chinese industrial software industry, strategies and routes for independent R&D of industrial software, development strategies for industrial software in the cloud era, the construction of application systems for industrial software in enterprises, and support and application solutions in the fields of digital transformation and digital twins; it analyzes various problems, contradictions, and misconceptions in the development of the Chinese industrial software industry, and proposes targeted strategic recommendations and solutions; it provides specific practical experiences and methodologies for challenging areas in industrial software, especially in engineering simulation and industrial R&D.
 Video Channel “Snow Forum” What seems to be a bottleneck is industrial software, but in fact, it is mathematics and physics.
Video Channel “Snow Forum” What seems to be a bottleneck is industrial software, but in fact, it is mathematics and physics.
Follow the “Snow Forum” video channel
Don’t miss the wonderful content

Join the WeChat Group of “Snow Forum”
Exchange and share together in the group


Media Cooperation, Reprint and Exchange



