This article contains 3085 words, 7 images, and 2 related articles, with a recommended reading time of 15 minutes.
This issue shares an article that focuses on high-order diffusion models, including DTI, DKI, DSI, HARDI, NODDI, and IVIM.


The magnetic resonance diffusion imaging technology is currently the only method for measuring the diffusion movement of water molecules in vivo. The most common technique is Diffusion Weighted Imaging (DWI), which everyone is likely familiar with. Therefore, this article will focus on some common or highly regarded high-order diffusion models, including DTI, DKI, DSI, HARDI, NODDI, and IVIM.
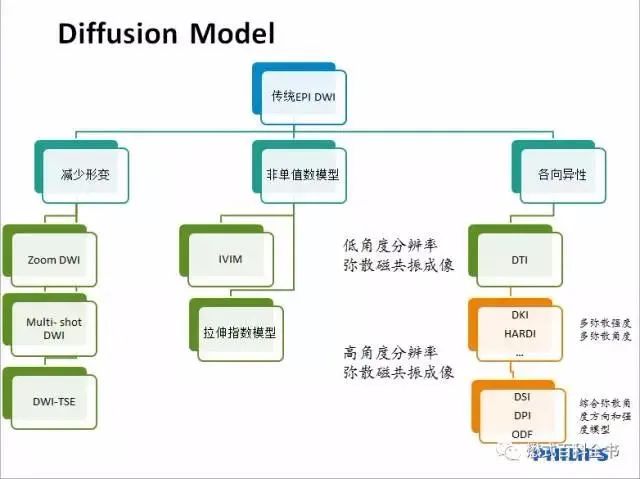
The following image is an overview of the development of diffusion MRI, which allows for a general and intuitive understanding of the evolution of diffusion (This image is sourced from the Encyclopedia of Mow). The basic theory will not be introduced in this issue; we will directly present the key content.

1. DTI
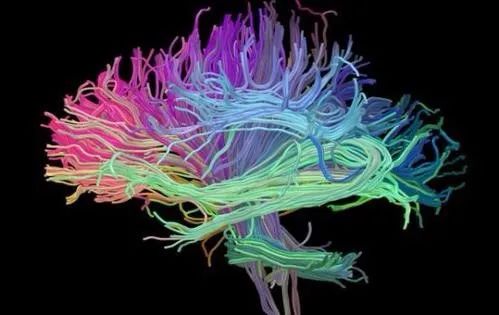
Diffusion Tensor Imaging (DTI) is the most commonly used high-order diffusion model based on Diffusion Weighted Imaging (DWI). It is also a non-invasive examination method that effectively observes and tracks brain white matter fiber bundles, accurately reproducing the orientation information of nerve fiber bundles. DTI mainly studies Gaussian diffusion, using three eigenvectors to represent the three directional components of diffusion. The principal direction component is along the tangent direction of the nerve fiber orientation, while the other two are normal directions, which depict the diffusion patterns of water molecules constrained by the white matter nerve synapses, thereby distinguishing between cerebrospinal fluid and synaptic regions. However, it is not very sensitive to gray matter regions. In terms of brain nerve fiber bundles, DTI has become the mainstream method (although visceral nerves can also be studied, but that is a later discussion). However, DTI has a significant limitation: due to technical constraints, it cannot identify multiple fiber directions within a single voxel. In more complex neural system studies, if we cannot explore the directions and complexities of the nerves, we cannot meet our needs for exploring the unknown. For this, we have other models to choose from, such as…
2. DKI
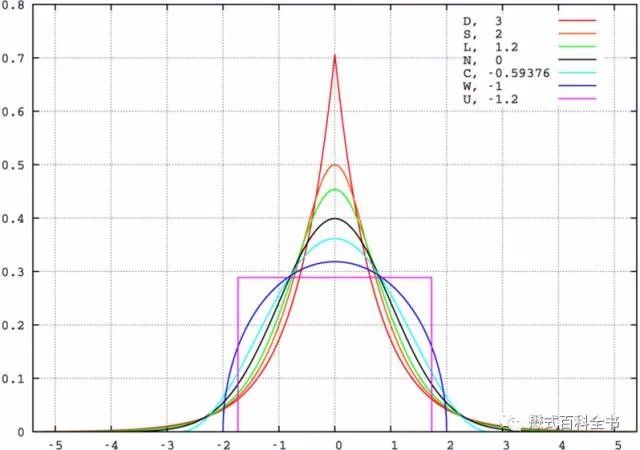
That’s right, we also have Diffusion Kurtosis Imaging (DKI). Kurtosis, also known as the kurtosis coefficient, characterizes the height of the peak of a probability density distribution curve at the mean value. Intuitively, kurtosis reflects the sharpness of the peak, defined as the fourth cumulant divided by the square of the second cumulant. It equals the fourth central moment divided by the square of the variance of the probability distribution minus 3, which is also called excess kurtosis (subtracting 3 makes the kurtosis of Gaussian distribution equal to 0). The above image also comes from the Encyclopedia of Mow. The theoretical basis of DTI assumes that water molecules diffuse in biological tissues as anisotropic or isotropic Gaussian random distributions, thus displaying relatively uniform structures of white matter (as mentioned earlier, it is not very sensitive to gray matter because the nerve fiber directionality in gray matter is more complex). However, in reality, simply using isotropic or anisotropic diffusion is insufficient to express the complex system characteristics of the human body. The Gaussian model’s single-exponential diffusion tensor model struggles to obtain precise organizational structure characteristics. To more accurately reveal the microstructural characteristics of tissues, diffusion models studying microstructures must evolve toward higher-order complexities. In terms of brain tissue, the diffusion of water molecules is actually non-Gaussian distribution, especially for the highly complex structure of brain gray matter. As shown in the above image, some probability density distribution curves have higher and sharper peaks, more slender, and converge towards the middle; while others have more blunt and rounded peaks, wider, and spread outwards. Kurtosis reflects the complexity of nerve fiber structures (DTI only reflects directionality), the higher the kurtosis, the more complex the nerve fiber structure, and the more significant the constraints on non-Gaussian distributed water molecule diffusion. DKI can better reflect the complex directional nerve fiber structures, compensating to some extent for the shortcomings of DTI.
3. DSI

Unlike DTI, which cannot identify the complex directionalities of nerve fibers within a specific voxel, Diffusion Spectrum Imaging (DSI, also known as Q-space Imaging) can identify multiple fiber directions within a voxel. DSI does not rely on any computational model; it uses diffusion displacement for three-dimensional Fourier encoding, allowing for the direct calculation of the three-dimensional probability density distribution of water diffusion displacements within a voxel, thereby reproducing the complex characteristics of fiber bundle directions. DSI has more precise spatial resolution capabilities, bridging the gap between micro and macro scales, and providing possibilities for further exploration and integration of multi-scale analysis research at the cellular and subcellular levels. In other words, DSI is more suitable for imaging studies of fine structures. However, DSI also has certain drawbacks: 1. low sampling efficiency, 2. large volume of sampling data, 3. high b-value requirements, 4. high gradient and acquisition time requirements, etc. These limitations may be constrained by the performance of the equipment itself or the conditions during practical operations, ultimately hindering its clinical application. Thus, we have another alternative, which is HARDI.
4. HARDI
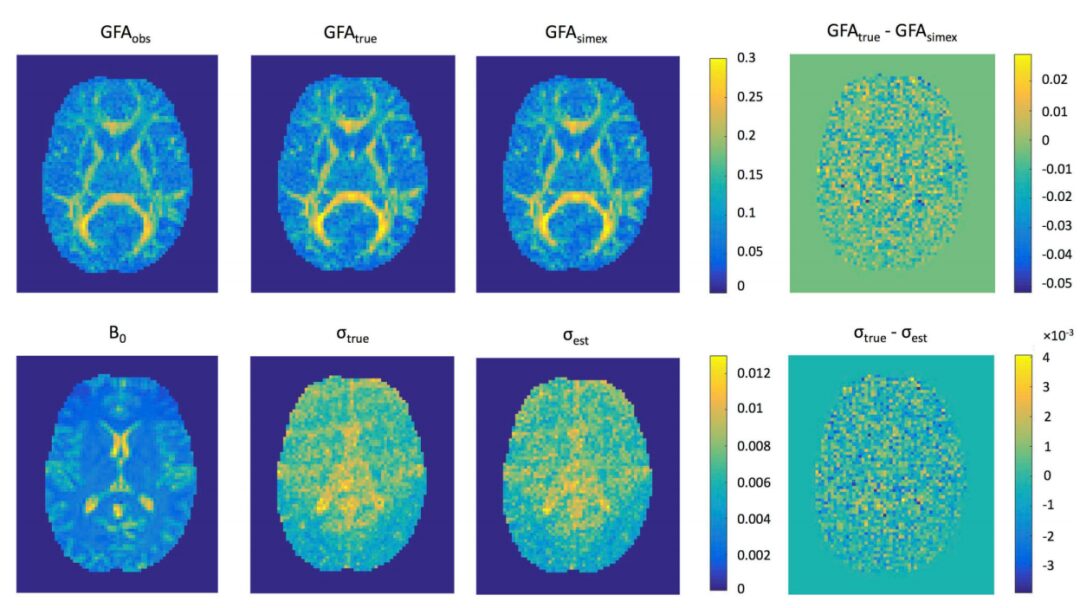
High Angular Resolution Diffusion Imaging (HARDI) can also reflect the complexity of nerve fiber direction distribution. It requires more angles and higher b-values than DTI. Although it primarily depicts the anisotropy of nerve fiber bundles, it can provide sufficient information about their directional complexity. Similar to how DTI uses FA (Fractional Anisotropy) as an important parameter, HARDI uses GFA (General Fractional Anisotropy) as a parameter. Compared to DTI, HARDI is more suitable for studying the connectivity and changes of brain neural structures. As a diffusion model, HARDI does not have as high requirements as DSI; it merely requires a few more scanning angles and a slightly higher b-value.
5. NODDI
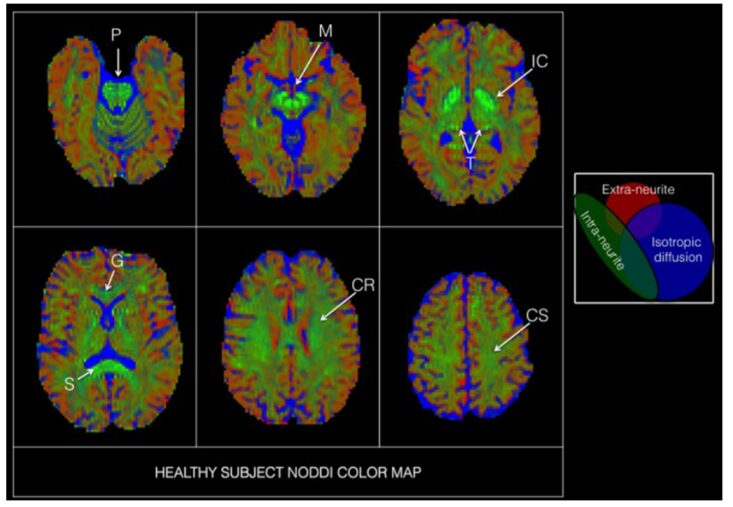
The models mentioned earlier either consider whether the diffusion of water molecules is “anisotropic” or whether the diffusion “satisfies Gaussian distribution.” For example, DTI mainly studies Gaussian diffusion, which is used to distinguish between cerebrospinal fluid and synaptic regions; DKI primarily studies non-Gaussian diffusion, which distinguishes between cerebrospinal fluid and extra-synaptic regions. Neurite Orientation Dispersion and Density Imaging (NODDI) considers both the “anisotropic” nature of water molecule diffusion and whether it “satisfies Gaussian distribution.” By distinguishing between freely diffusing water molecules (isotropic Gaussian diffusion, such as cerebrospinal fluid, CSF), intra-synaptic water molecule diffusion (anisotropic non-Gaussian diffusion, restricted diffusion), and extra-synaptic water molecule diffusion (anisotropic Gaussian diffusion, obstructed diffusion), it can simultaneously categorize brain space into cerebrospinal fluid, extra-synaptic, and intra-synaptic subspaces for research, and quantitatively study the volume fractions of each subspace, making it more suitable for quantitative analysis of whole brain space. NODDI, like HARDI, requires more scanning angles than DTI, but the difference is that HARDI requires high b values, while NODDI requires multiple b values, with at least one being a high b value. Ultimately, NODDI not only reflects the directionality of nerve fibers but also considers the changes in nerve synapse density. The directionality of nerves can reflect their connectivity, while density reflects their complexity. Both play different roles in brain function research; for example, complexity can reflect neurodegenerative changes with age, while connectivity more reflects functional lesions, etc.
6. IVIM

The previous five models focus on the orientation and complexity of nerve fibers, while Intro-Voxel Incoherent Movement (IVIM) aims to reflect perfusion-related disease information, primarily applied in liver cancer, liver fibrosis, kidney tumors, prostate cancer, peripheral lung cancer, cervical cancer, and breast diseases, and can also be applied to brain gliomas, nasopharyngeal cancer, and cerebral infarction in clinical research. Like DKI, which can reflect fine neural fiber structures, IVIM has three important parameters: the fast diffusion coefficient (D*) reflects microcirculation perfusion, while the slow diffusion coefficient (D) reflects the diffusion of water molecules inside and outside cells, and the perfusion fraction (f) reflects blood flow. Compared to other models, IVIM requires a relatively large number of b-values, which may require as many as 18 b-values. In IVIM applications, the number and size of b-values directly affect the accuracy of the final measurement results. Despite its stringent requirements, it is currently one of the most noteworthy clinical research methods.

Follow the Encyclopedia of Mow for more exciting original content.
Welcome to subscribe to my WeChat Official Account (personal blog).
Добро пожаловать в мой блог WeChat.

Copyright Statement:
The copyright belongs to “Encyclopedia of Mow.” Personal collection, forwarding, and sharing are welcome. Any other media, websites, public accounts, platforms, or forums wishing to reprint or quote must obtain authorization. Unauthorized use is prohibited! After obtaining authorization, it must be noted in a prominent position “Reprinted from: Encyclopedia of Mow,” and the original link to my article must be set at the reading original place, allowing readers to return to my original article. Thank you all for your support! Sincerely, the author!