GESP Programming Ability Certification Standards from Level 1 to Level 8 (Syllabus)
Download link:https://gesp.ccf.org.cn/101/1008/10012.htmlLevel 3 Knowledge Content (C++)
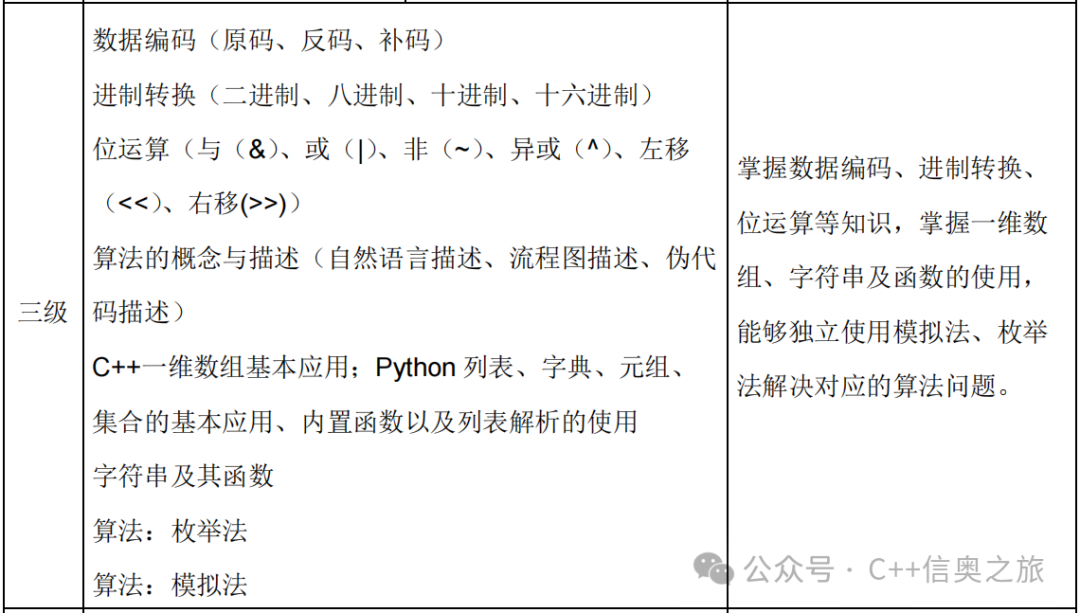The following is a detailed explanation of these knowledge points based on the GESP Level 3 C++ programming language syllabus:1. Data Encoding (Original Code, Inverse Code, Complement Code)
1. Original Code
Original code is the most intuitive encoding method. For an integer, its original code representation is simply converting the absolute value of the integer to binary, with the highest bit as the sign bit (0 for positive, 1 for negative). For example, the original code of positive 5 is 00000101, and the original code of negative -5 is 10000101. The advantage of original code is its simplicity, but it has a serious problem: there are two zeros (+0 and -0), which complicates processing in computers.
2. Inverse Code
To solve the representation problem of zero in original code, inverse code was introduced. The definition of inverse code is: the inverse code of a positive number is the same as its original code, while the inverse code of a negative number is obtained by inverting all bits of its original code except the sign bit (i.e., 0 becomes 1, and 1 becomes 0). For example, the inverse code of positive 5 is still 00000101, while the inverse code of negative -5 is 11111010. Inverse code still has some operational inconveniences, especially in addition operations.
3. Complement Code
Complement code was designed to solve the problems of inverse code in addition operations. The definition of complement code is: the complement code of a positive number is the same as its original code, while the complement code of a negative number is its inverse code plus 1. For example, the complement code of positive 5 is 00000101, and the complement code of negative -5 is 11111011 (inverse code 11111010 plus 1). The advantage of complement code is that it can convert subtraction operations into addition operations, thus simplifying the hardware design of computers. For example, calculating 5-3 can be transformed into 5+(-3) in complement code, which is 00000101+11111101, resulting in 00000010, which is 2.
Therefore, in computer systems, integers are usually stored and operated in complement code.
2. Base Conversion (Binary, Octal, Decimal, Hexadecimal)
1. Binary (Binary)
Binary is the numeral system used internally by computers, where each digit has two possible values: 0 and 1. The base of binary is 2, and the weight of each digit is a power of 2. For example, the binary number `1011` can be converted to decimal as `1×2³ + 0×2² + 1×2¹ + 1×2⁰ = 11`.
In C++, binary numbers are usually prefixed with `0b` or `0B`. For example, `0b1011` represents the binary number `1011`.
2. Octal (Octal)
The base of octal is 8, and each digit can take values from 0 to 7. The weight of each digit in octal is a power of 8. For example, the octal number `123` can be converted to decimal as `1×8² + 2×8¹ + 3×8⁰ = 83`.
In C++, octal numbers are prefixed with `0` (note it is the digit 0). For example, `0123` represents the octal number `123`.
3. Decimal (Decimal)
Decimal is the numeral system we use most commonly in daily life, where each digit can take values from 0 to 9, and the weight of each digit is a power of 10. For example, the decimal number `123` represents `1×10² + 2×10¹ + 3×10⁰`.
In C++, decimal numbers have no special prefix and can be written directly. For example, `123` represents the decimal number `123`.
4. Hexadecimal (Hexadecimal)
The base of hexadecimal is 16, and each digit can take values from 0 to 15, where 10 to 15 are represented by letters A to F (or a to f). The weight of each digit in hexadecimal is a power of 16. For example, the hexadecimal number `1A3` can be converted to decimal as `1×16² + 10×16¹ + 3×16⁰ = 419`.
In C++, hexadecimal numbers are prefixed with `0x` or `0X`. For example, `0x1A3` represents the hexadecimal number `1A3`.
5. Base Conversion Methods
1) Conversion between Binary and Decimal:
• Binary to Decimal: Expand the binary number by bits, multiply by the corresponding weight (power of 2), and then sum.
• Decimal to Binary: Use the “divide by 2 and take remainder” method, continuously divide the decimal number by 2 until the quotient is 0, then arrange the remainders in reverse order.
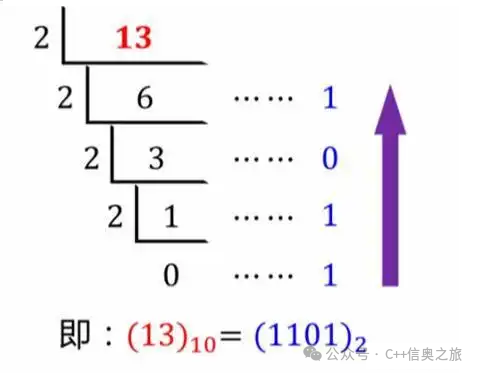
2) Conversion between Binary and Octal, Hexadecimal:
• Binary to Octal: Group every 3 bits from right to left, padding with 0 if there are not enough bits, then convert each group of binary numbers to the corresponding octal number.
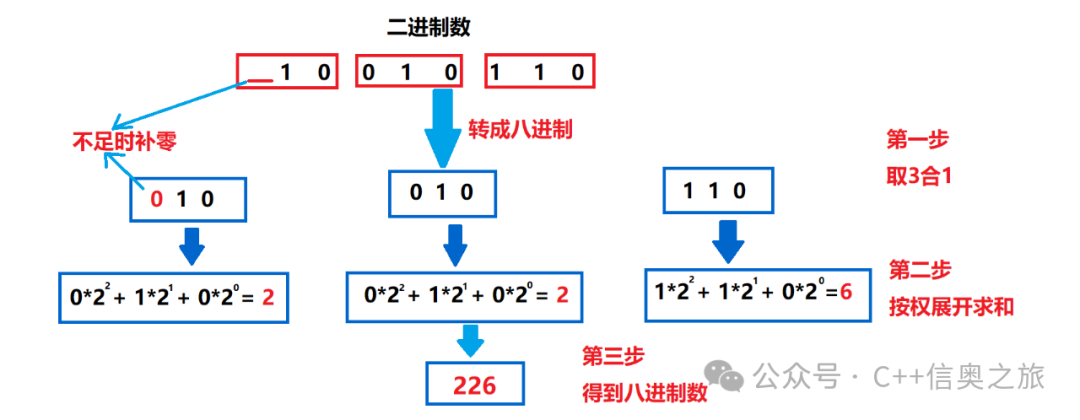
• Binary to Hexadecimal: Group every 4 bits from right to left, padding with 0 if there are not enough bits, then convert each group of binary numbers to the corresponding hexadecimal number.
3. Bitwise Operations (&, |, ~, ^, <<, >>)1. Introduction to Bitwise Operators1) Bitwise AND (&) The bitwise AND operator “&” is used to perform a logical AND operation on each bit of two integers. The result bit is 1 only when both corresponding bits are 1; otherwise, it is 0.2) Bitwise OR (|) The bitwise OR operator “|” is used to perform a logical OR operation on each bit of two integers. The result bit is 1 if at least one of the corresponding bits is 1; otherwise, it is 0.3) Bitwise XOR (^) The bitwise XOR operator “^” is used to perform a logical XOR operation on each bit of two integers. The result bit is 1 when the corresponding bits are different; otherwise, it is 0.4) Left Shift (<<) The left shift operator “<<” is used to shift the binary representation of an integer to the left by a specified number of bits. When left shifting, high bits are discarded, and low bits are filled with 0.5) Right Shift (>>) The right shift operator “>>” is used to shift the binary representation of an integer to the right by a specified number of bits. When right shifting, for unsigned numbers, high bits are filled with 0; for signed numbers, high bits are filled with the sign bit (sign bit extension).2.Swapping Variables Using XOR
3.Left Shift for Multiplication
4. Concept and Description of Algorithms1. Five Basic Characteristics of Algorithms:
- Finiteness: An algorithm must terminate after a finite number of steps and cannot loop indefinitely.
- Determinacy: Each operation in the algorithm must be clear and unambiguous.
- Feasibility: Each operation in the algorithm must be executable and not abstract or impossible to implement.
- Input: An algorithm can have zero or more inputs, which are the initial conditions for the algorithm’s execution.
- Output: An algorithm must have one or more outputs, which are the results of the algorithm’s execution.
Methods for Describing Algorithms Algorithms can be described in various ways, commonly using natural language, pseudocode, flowcharts, and programming languages. Among them, pseudocode is a description method that lies between natural language and programming language, using concise statements to describe the logical structure of the algorithm, making it easy to understand and convenient to convert into actual program code.2. Pseudocode ExampleDescribing the Euclidean algorithm for finding the greatest common divisor (GCD) of two numbers:
1. Input two non-negative integers a and b
2. If a < b, swap the values of a and b
3. While b is not equal to 0, perform the following steps:
a. Calculate the remainder of a divided by b, denoted as r
b. Assign the value of b to a
c. Assign the value of r to b
4. Output a, which is now the greatest common divisor
5. Basic Applications of C++ One-Dimensional Arrays1. Definition of One-Dimensional Arrays A one-dimensional array is a collection of elements of the same data type, stored contiguously in memory. Each element in the array can be accessed via an index.The syntax for declaring a one-dimensional array is: type name[length];The length of the array must be a constant expression at the time of declaration, indicating the number of elements in the array.2. Introduction to Indexing The index of an array starts from 0, meaning the index of the first element is 0, the second element is 1, and so on. For an array of length n, the index range is from 0 to n-1.3. Initializing ArraysArrays can be initialized at the time of declaration or assigned values one by one in subsequent code.
Initialization at declaration: int arr[5] = {1, 2, 3, 4, 5}; // Initialize array
Assigning values one by one: int arr[5];
for (int i = 0; i < 5; i++) {
arr[i] = i + 1; // Assign array elements values from 1 to 5
}
4. Common Array Operations
- Sum: Calculate the sum of all elements in the array.
- Find Maximum: Find the maximum value in the array.
- Reverse Array: Reverse the order of elements in the array.
6. Strings and Their FunctionsC++ provides two main ways to handle strings: character arrays (C-style strings) and std::string class objects.1. Character Arrays (C-style Strings)
Character arrays are the basic way to handle strings in C, storing strings in the form of character arrays, with a null character ‘ ’ as the end marker.
Declaration and Initialization
char str1[10] = “Hello”; // Declare a character array of length 10 and initialize
char str2[] = “World”; // Compiler automatically calculates length
Common C String Functions
- strlen(array name): Calculate the length of the string (excluding the end marker ‘ ’)
- strupr(array name): Convert lowercase letters in the character array to uppercase
- strlwr(array name): Convert uppercase letters in the character array to lowercase
- strcpy(array name1, array name2): Copy one string to another
- strcat(array name1, array name2): Append one string to the end of another
- strcmp(array name1, array name2): Compare two strings.
2. std::string Class Objects The std::string class in the C++ standard library provides more powerful and flexible string manipulation capabilities. Using std::string can avoid common errors in C-style strings, such as memory overflow.
Declaration and Initialization
#include <string>
std::string str1 = “Hello”; // Initialize using string literal
std::string str2(“World”); // Initialize using constructor
std::string str3(str1); // Initialize using another string object
Common Member Functions
- size() or length(): Get the length of the string.
- find(substring subs, [starting position pos]): Find the position of the substring; if not found, return std::string::npos.
- substr(start position i, substring length): Get the substring.
- compare(string name): Compare two strings.
- insert(): Insert characters or strings.
- replace(): Replace substring; if the length of the source data being replaced is not equal to the length of the data being replaced, the length of the resulting string changes.
- erase(): Delete 1 character or a segment of characters
- clear(): Clear the content of the string.
3. String ApplicationsUsing string.find, string.substr, string.erase to propose passwords.
7. Algorithms (Enumeration Method, Simulation Method)1. Enumeration Method The enumeration method is a way to find solutions to problems by traversing all possible cases. It is suitable for problems with a limited solution space that can be directly enumerated. The key to the enumeration method is to clearly define the range of the solution space and check each possible solution one by one to see if it meets the conditions.
Example Problem: Find all numbers between 1 and 100 that can be divided by both 3 and 5.
2. Simulation Method The simulation method is a way to find solutions to problems by simulating the actual process of the problem. It is suitable for problems that need to be executed step by step according to certain rules. The key to the simulation method is to accurately implement the rules and logic described in the problem.Example Problem: Simulate a simple “Rock-Paper-Scissors” game, where the user inputs an option (rock, scissors, or paper), the program randomly generates an option, and then determines the winner.
8. STL (vector, list, map, bitset)1. vector vector is one of the most commonly used data structures in STL, which is a dynamic array that can automatically adjust its size. It supports random access, and insertion and deletion operations at the tail are efficient, but they are less efficient in the middle or at the head.
2. list list is a doubly linked list that supports efficient insertion and deletion of elements at any position but does not support random access. It is suitable for scenarios where frequent insertion or deletion of elements in the middle is required.3. map map is a collection of key-value pairs, where keys are unique and support fast lookup. It is commonly used in scenarios where quick access to values based on keys is needed.
4. bitset bitset is a fixed-size set of bits that can efficiently store and manipulate bits. It is commonly used for bitwise operations and state representation.
Summary
- vector: Dynamic array, supports random access, suitable for scenarios requiring frequent access to elements.
- list: Doubly linked list, suitable for scenarios requiring frequent insertion or deletion of elements in the middle.
- map: Collection of key-value pairs, supports fast lookup, suitable for scenarios requiring access to values based on keys.
- bitset: Set of bits, suitable for bitwise operations and state representation.