1. Introduction to PID Algorithm
The position PID, also known as the full-scale PID, is an acronym for Proportional, Integral, and Differential. It is a closed-loop control algorithm that integrates the three elements of proportional, integral, and differential control. It is currently one of the most mature control algorithms in continuous control systems and plays a crucial role in various fields such as industrial control, robotics, drones, robotic arms, and balance vehicles. This control algorithm emerged in the 1930s and 1940s and has remained relevant to this day, suitable for situations where the model of the controlled object is not well understood. Both practical experience and theoretical analysis have shown that applying this control law to many industrial processes yields satisfactory results. The essence of PID control is to perform proportional, integral, and differential operations on the error between the target value and the actual value, and use the result to influence the output.
The ideal PID control law for continuous control:
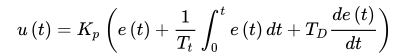
Editor
-
Kp——Proportional gain, Kp is inversely related to the degree of proportionality.
-
Tt——Integral time constant.
-
TD——Differential time constant.
-
u(t)——Output signal of the PID controller.
-
e(t)——Error between the set value r(t) and the measured value.
Proportional (P)
Proportional control is the simplest form of control, reacting proportionally to the deviation signal between the input and output of the control system. As soon as a deviation occurs, control action is immediately taken to reduce the error. The output of the proportional controller is directly proportional to the input, allowing for a rapid response to deviations. The speed at which the deviation decreases depends on the proportional coefficient Kp; a larger Kp results in a faster reduction of the deviation, but it can easily cause oscillations. Reducing Kp decreases the likelihood of oscillations but slows down the adjustment speed. Pure proportional control has an unavoidable static error, which requires integral control to address.
Integral (I)
Static errors generated in the proportional control phase are primarily eliminated in the integral phase, which aims to improve the system’s zero-error state. The strength of the integral action depends on the integral time constant Ti; a larger Ti results in a weaker integral action, and vice versa. The existence of integral control action is related to the duration of the deviation e(t); as long as there is a deviation in the system, the integral phase will continuously act, integrating the input deviation, causing the output of the controller and the actuator’s opening to change continuously, thus exerting control to reduce the deviation. With sufficient integral time, static errors can be completely eliminated, and the integral control action will remain unchanged. A smaller Ti results in a faster integral speed and a stronger integral action. However, if the integral action is too strong, it can lead to increased overshoot and even cause system oscillations.
Differential (D)
The role of the differential phase is to reflect the trend of change in the system’s deviation, or the rate of change. It can introduce an effective corrective signal before the error occurs, which helps improve the speed of output response, reduce overshoot of the controlled quantity, and increase system stability. Although the integral phase can eliminate static errors, it reduces the system’s response speed, making the introduction of a differential controller necessary, especially for controlled objects with significant inertia, where using a PI controller may not yield good dynamic adjustment quality, leading to large overshoots and oscillations. In such cases, differential action can be introduced. At the moment a deviation appears or changes, not only is a timely response made based on the deviation amount (i.e., proportional control action), but a larger control action is also provided based on the trend of change in the deviation amount (speed) (i.e., differential control action), effectively eliminating the deviation at its inception. This significantly reduces the system’s dynamic deviation and adjustment time, improving the dynamic adjustment quality of the system. The differential phase helps reduce overshoot, overcome oscillations, accelerate the system’s response speed, and reduce adjustment time, thereby improving the system’s dynamic performance. However, if the differential time constant is too large, it can lead to system instability. A significant drawback of differential control action is its susceptibility to high-frequency noise, making it unsuitable for flow control systems with severe interference signals.
Example Analysis
(1) Consider a water tank filling example, where the water level can be observed in real-time, and the goal is to fill the tank from empty to a certain level, controlling only the size of the water faucet.
To fill the tank, you only need to observe the distance between the actual water level and the target position. If the distance is large, open the faucet wider; if the distance is small, reduce the faucet opening. As the distance decreases, eventually closing the faucet will achieve the goal of filling the tank. For this simple system, only proportional adjustment is needed;
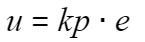
Editor
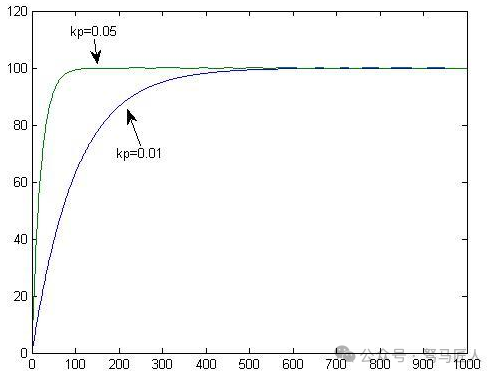
Kp represents the size of the water faucet; the larger the faucet, the faster the adjustment, meaning increasing the proportional coefficient can speed up the system’s response.
Editor
(2) Building on the previous example, not only is water needed to fill the tank, but continuous water supply to the user is also required. Therefore, a constant term needs to be added to the original mathematical model, as follows:
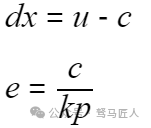
Editor
If the controller only uses a proportional phase for adjustment, when the system is in a steady state, meaning the speed of water outflow equals the speed of water inflow, dx = 0, it can be deduced that the relationship of e will not be zero when the system is stable, resulting in a slight difference in liquid level height, which is the system’s static error.
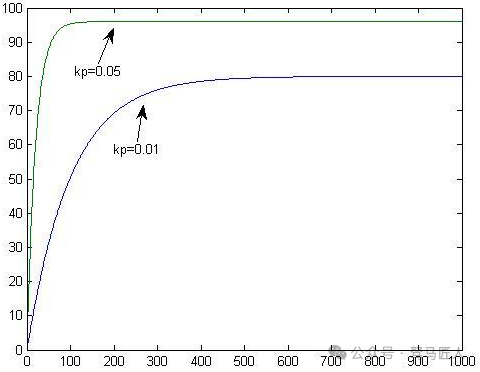
When c is a fixed constant, increasing kp will reduce e, meaning in the presence of static error, increasing the proportional coefficient helps reduce static error;
As shown in the following figure:
Editor
However, if the user’s water consumption is not a constant, controlling the static error becomes challenging, necessitating increased dynamicity in water supply. This cannot be achieved with proportional control alone; integral adjustment is required.
Editor
This is equivalent to adding another faucet, which operates under the rule that when the water level is below the target height, it is opened wider, and when the water level is above the target height, it is closed. If the user’s water consumption remains constant, after several adjustments, the system’s static error can be eliminated; this is how the integral phase can eliminate the system’s static error.
With the addition of the integral adjustment phase, another important parameter is integral time; see the following figure:
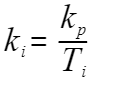
Editor
From the above equation, it can be seen that a larger integral time will lead to a smaller adjustment by the integral phase, effectively reducing the sensitivity of integral adjustment. In the example, this can be understood as replacing the water pipe of the faucet with a thinner one. Before reaching the predetermined height, the second faucet will inject water into the tank at maximum capacity. When the expected height is reached, the faucet will be fully opened, naturally leading to an overfilling phenomenon, where the excess amount is the overshoot; thus, the larger the second faucet, the faster it reaches the expected height, but the more fluctuations occur. As shown in the following figure:
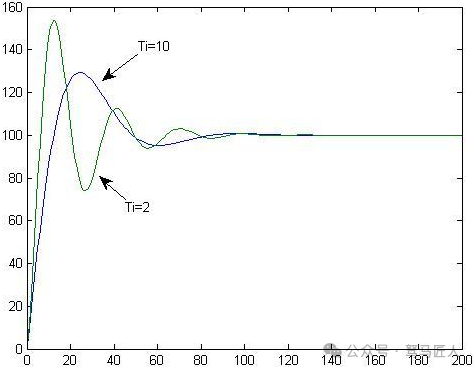
Editor
Therefore, the conclusion can be drawn: increasing the integral time helps reduce overshoot, increases system stability, but will prolong the time to eliminate static error.
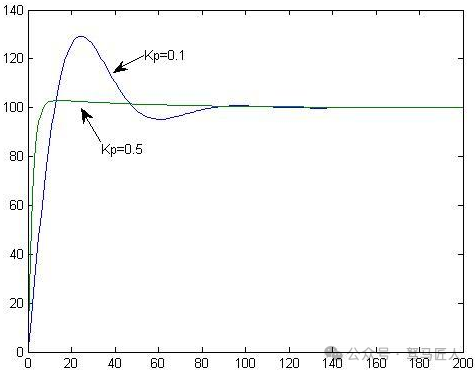
(3) If the user’s water consumption is not a constant but a variable, then the second faucet’s control based on the expected height becomes somewhat delayed, as it is difficult to predict the user’s water consumption in the next time period. In this case, merely using proportional and integral adjustments may not be effective, necessitating the introduction of differential adjustment. This is equivalent to adding another faucet and a controllable valve that can leak; now, it is necessary to observe the rate of change in water level and adjust the speed of water outflow/inflow based on the rate of change in the actual height versus the expected height to achieve better control of the water level. The effect is shown in the following figure:
Editor
2. C Language Implementation of Position PID
Define Structure
/*pid*/ typedef struct { float target_val; // Target value float actual_val; // Actual value float err; // Define deviation value float err_last; // Define last deviation value float Kp,Ki,Kd; // Define proportional, integral, and differential coefficients float integral; // Define integral value }_pid;PID Parameter Initialization
/** * @brief PID parameter initialization * @note None * @retval None */ void PID_param_init(){ /* Initialize parameters */ printf("PID_init begin \n"); pid.target_val=0.0; pid.actual_val=0.0; pid.err=0.0; pid.err_last=0.0; pid.integral=0.0; pid.Kp = 0.31; pid.Ki = 0.070; pid.Kd = 0.3; printf("PID_init end \n"); }This function primarily initializes all parameters of the PID, including the three parameters Kp, Ki, and Kd, as these directly affect the time and state in which the algorithm reaches the target value.
Implementation of PID
/** * @brief Implementation of PID algorithm * @param val Actual value * @note None * @retval Output after PID calculation */float PID_realize(float temp_val){ /* The target value only participates in the calculation here, calculating the error between the target value and the actual value */ pid.err=pid.target_val-temp_val; /* Error accumulation */ pid.integral+=pid.err; /* Implementation of PID algorithm */ pid.actual_val=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid.err-pid.err_last); /* Error transmission */ pid.err_last=pid.err; /* The returned value is the value after PID operation */ return pid.actual_val;}Setting the Target Value
/** * @brief Set target value * @param val Target value * @note None * @retval None */void set_pid_target(float temp_val){ pid.target_val = temp_val; // Set the current target value}The following function should be called within the loop, and the set_pid_target() function should be called beforehand to set the target value.
/** * @brief Timer periodic call function * @param None * @note None * @retval None */ void time_period_fun(){ static int num=0; static int run_i=0; if(!pid_status) { float val=PID_realize(pid.actual_val); int temp = val; // Send actual value to channel 1 set_computer_value(SEED_FACT_CMD, CURVES_CH1, &temp, 1); } }