
The Programme for International Student Assessment (PISA), initiated by the Organisation for Economic Co-operation and Development (OECD) in 2000, is the largest and most influential international education evaluation. It tests 15-year-old students from various countries who are receiving basic education. The PISA 2021 Mathematics Literacy Assessment Framework (as shown in the figure) adjusts the definitions, connotations, and assessment content of mathematical literacy, treating it as a basis for evaluating an individual’s ability to reason mathematically in different real-world contexts, express, apply, and interpret mathematical reasoning during problem-solving. The assessment framework strengthens the examination of students’ ability to handle complex information in real situations; it highlights the core role of mathematical reasoning in the mathematical modeling process, increases the scoring weight of mathematical reasoning, emphasizes that mathematics is fundamentally aimed at solving problems, underscores the connection between content areas and mathematical modeling, and incorporates 21st-century skills, clarifying the goals of a “21st-century citizen”. In the coming years, this new definition of mathematical literacy will influence basic mathematics education globally.
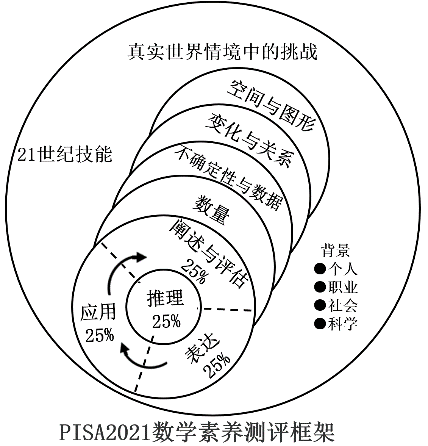
By studying the PISA 2021 Mathematics Literacy Assessment Framework in depth and understanding the definitions, connotations, and assessment content of mathematical literacy, we can better grasp the development direction of mathematics education reform. If we view the design of primary school math problems from the perspective of PISA assessments, we can gain a higher-level insight into the relationship between mathematics education, assignment design, and the cultivation of core mathematical literacy. Below, I will discuss our practices and thoughts on designing primary school math problems under the PISA 2021 Mathematics Literacy Assessment Framework from four aspects.
1. Create Realistic Situational Problems to Improve Problem-Solving Skills
The PISA 2021 Mathematics Literacy Assessment Framework categorizes mathematical situations into personal, social, occupational, and scientific contexts. As the cognitive distance from students increases from personal to scientific contexts, their familiarity gradually decreases, but the requirements for cognition and understanding deepen. Problem design should enhance the authenticity of situations, strengthen the connection between mathematical knowledge and real-life contexts, starting from simple and direct everyday tasks, beginning with personal situational problems, gradually increasing the complexity of situations, and ultimately reaching high-level scientific contexts, reflecting the essence of the mathematics discipline. Based on the learning situation of primary school students, the design of math problems should primarily focus on creating personal and social situational problems.
Problem 1 (Grade 3)
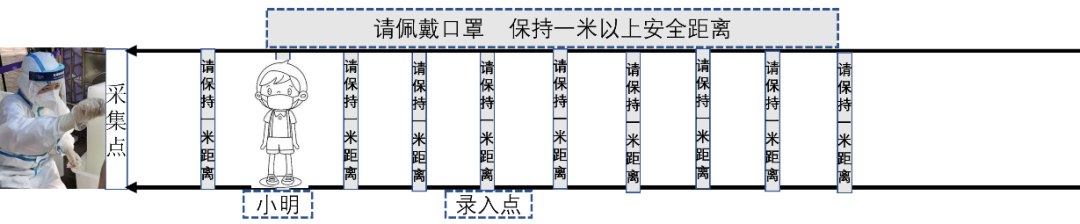
The commonly used “ten-in-one mixed sampling” nucleic acid test collects samples from 10 individuals into one collection tube for testing, improving testing efficiency. The first person to hold the collection tube is referred to as the “tube leader”. Please mark the position of the next “tube leader” with an “▲” in the diagram and explain your reasoning.
Problem 2 (Grade 5)
To enhance physical fitness, Xiaohua runs around the perimeter of the Xiamen International Conference and Exhibition Center every day, as shown in the diagram. Estimate the approximate area of the Xiamen International Conference and Exhibition Center in square meters and explain how you made your estimation.
Problem 3 (Grade 6)
The “Moonlight Ring” landscape light in the Garden Expo Park, symbolizing “The bright moon rises over the sea, and at this moment, we share the same sky”, has an outer diameter of 36 meters and an inner diameter of 22 meters. What is the area of the “Moonlight Ring” in square meters?

Problem 4 (Grade 6)
The Mid-Autumn Festival Bo Bing legend was invented by the national hero Zheng Chenggong, using the results of throwing six dice into a large bowl to determine the prizes for participants, a unique custom activity during the Mid-Autumn Festival in Xiamen. The traditional prizes for Bo Bing are mooncakes of different sizes: 1 cake representing the top scholar (“Zhuangyuan”); 2 cakes representing the second place (“Dui Tang”); 4 cakes for the third place (“San Hong”); 8 cakes for the fourth place (“Si Jin”); 16 cakes for the fifth place (“Er Ju”); and 32 cakes for the sixth place (“Yi Xiu”). The basic rules of Bo Bing are as follows: After throwing six dice, if you get one red four, two red fours, or three red fours, you receive one “Yi Xiu”, “Er Ju”, or “San Hong” cake respectively; a “Zhuangyuan” cake is awarded for rolling four red fours, with the highest score from the other two dice determining the winner; “Si Jin” is awarded for rolling four of the same number excluding red fours; if all six dice show different numbers from one to six, you receive a “Dui Tang”. Detailed rules can be understood by scanning the right code. Can you use the mathematical knowledge you have learned to explain whether these rules are reasonable? If they are reasonable, please explain why. If not, please propose your improvement suggestions.
Problem 5 (Grade 6)
Xia, Yi, and Bing are carpooling. Their drop-off locations and distances are illustrated in the diagram. At the end of the trip, they paid a total of 100 yuan for the fare. Please help them design a reasonable payment scheme and calculate how much each passenger should pay.

2. Increase Mathematical Reasoning Problems to Highlight the Core Position of Mathematical Reasoning
The PISA 2021 Mathematics Literacy Assessment Framework places reasoning at its core, integrating mathematical reasoning throughout the problem-solving process, reflecting a focus on the essence of mathematics. In the primary stage, the emphasis is on reasoning awareness. In the specific expressions of reasoning ability in the PISA 2021 Mathematics Literacy Assessment Framework, we select five specific expressions with relatively low level requirements: “choose appropriate reasons”, “make simple summaries”, “explain the significance or lack thereof of a mathematical conclusion in a real problem”, “understand definitions, rules, and formal mathematical systems, and use algorithms and computational reasoning”, and “defend and explain the reasoning process, procedures, and simulations leading to a certain mathematical result or conclusion” to design common reasoning-type problems for primary school mathematics.
Problem 6 (Grade 3)
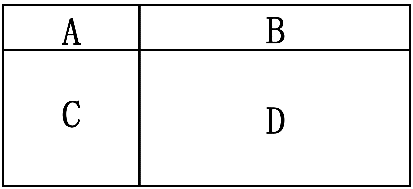
As shown in the figure, a rectangle is divided into four smaller rectangles. If the area of B is 10 square decimeters; C’s area is 15 square decimeters, and D’s area is 30 square decimeters, what is the area of A in square decimeters? Explain your reasoning.
Problem 7 (Grade 4)
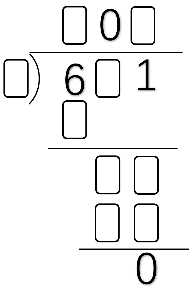
Based on the division equation on the right, you can deduce that the divisor must be ( ).
Problem 8 (Grade 4)
Observations of a planar figure are recorded as follows:
(1) It has four sides, with only one pair of opposite sides parallel.
(2) It has four angles, two of which are acute and two are obtuse.
(3) This figure can completely overlap its left and right sides when folded.
Based on these observations, the planar figure can be determined to be ( ).
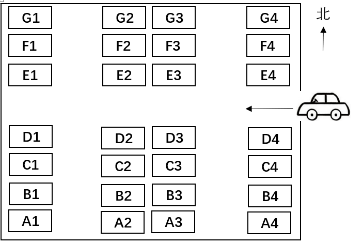
Problem 9 (Grade 4)
Dad drives into the parking lot from the arrow and heads west, turning south at the second intersection. Based on the parking position diagram, Dad could possibly park in ( ) position.
A.F2 B.F4 C.B2 D.B4
Problem 10 (Grade 4)
The survey results of the favorite TV programs among the students of Class 4, Grade 2 are as follows. The statistical chart that corresponds to the information represented by the results is ( ).

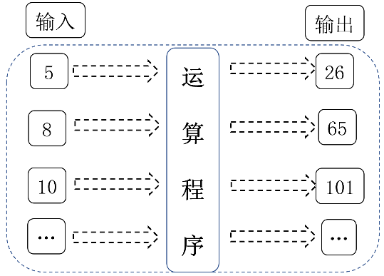
Problem 11 (Grade 5)
A programming software has an operation program, and the operation results are shown in the figure. Based on this operation program:
(1) If you input 6, what will the output be ( )?
(2) If you input ( ), what will the output be 82?
(3) What is the pattern of this operation program ( )?
Problem 12 (Grade 5)
Xiaoming said: If the sum of the digits in the unit, ten, and hundred places of a three-digit number is divisible by 3, then this number can also be divided by 3. Do you agree with his statement? Please explain your reasoning.
3. Conduct Comprehensive Practical Applications to Clarify the Fundamental Purpose of Problem Solving
The PISA 2021 mathematics literacy definition emphasizes that mathematics solves practical problems. According to the characteristics of students at different age stages, when designing realistic situational problems, it is important to guide students to comprehensively apply mathematical knowledge and interdisciplinary knowledge to solve problems, designing exploratory practices, project learning, and small research tasks (problems) that allow students to experience the entire process of discovering problems, raising questions, analyzing problems, and solving problems in real situational problems, thereby enhancing their ability to solve practical problems.
Problem 13 (Grade 6)
Comprehensive practical activity on Bo Bing culture.
Research background: In Xiamen, the Mid-Autumn Festival is comparable to the New Year. During this time, families organize dice games for Bo Bing, a unique folk culture in Xiamen.
(1) Explore Bo Bing culture. Collect and organize relevant information about Xiamen Bo Bing culture (such as historical origins, Bo Bing customs, evolution of prizes, Bo Bing tools, Bo Bing stories, interesting photos, etc.). Each family collaborates to complete the collection, and each family organizes the collected information into a slideshow to share in the class group, learning from each other, with students voting for the top 5 works to share in class (one week is allocated).
(2) Experience Bo Bing customs. Invite folk culture experts to introduce Xiamen Bo Bing culture and rules, share the latest Bo Bing rules with students, and organize students into groups to experience the Bo Bing folk activity according to the rules (two class periods are allocated).
(3) Study Bo Bing rules. Assign exploratory homework requiring students to investigate whether the Bo Bing rules are reasonable from a mathematical perspective in groups. If difficulties arise, they can invite parents to participate in the study. Try to write the research process and results into a math diary or research paper and create a slideshow to report in class (two weeks are allocated).
Problem 14 (Grade 6)
“Little Financial Manager” comprehensive practical activity.
Research background: During the Spring Festival, students receive a lot of red envelopes, plus their saved pocket money, most students have a significant amount of wealth.
(1) Design a driving question: If you were to be a little financial manager, how would you manage your wealth correctly to ensure steady growth?
Discussion: What knowledge areas need to be researched to address this question? What channels can be notified to obtain information? What difficulties might be encountered? What assistance might be needed? Based on the discussion results, groups will collect and organize information, creating a slideshow to share within the group (one week is allocated).
(2) Arrange for excellent works to be shared in class; invite financial experts to answer students’ questions, discussing and summarizing how to achieve steady growth in wealth and what points need attention (two class periods are allocated).
(3) Design a personal wealth management plan, explaining the rationale behind the plan (three days are allocated).
(4) Exchange personal wealth management plans within the group, evaluate each other, and adjust individual wealth management plans based on classmates’ feedback. “Show off” the adjusted personal wealth management plans (two days are allocated).
(5) Based on your personal wealth management plan, experience related services such as opening accounts and financial management (one week is allocated).
(6) Collect wealth income data to verify whether the personal wealth management plan is reasonable. Independent reflection: Did my wealth achieve steady growth? What might be the reasons? Write a research report for group exchange (two months later, near graduation).
(7) Micro-lesson learning on the design of “personal wealth management plans” (one day is allocated).
(8) Assign summer homework: Based on your practical research conclusions, design a wealth management plan of 30,000 yuan for a selected group, considering “complete structure”, “appropriate plan”, and “aesthetic design”.
Designing such a long-term comprehensive practical task allows students to experience the process of “collecting information – sharing and communicating – expert guidance – practical experience – summarizing and organizing – innovative application”. In this practical application that students personally experience, problem-solving drives students’ autonomous learning, enhancing their comprehensive literacy.
4. Implement Advanced Problem Design to Realize the Evaluation Orientation of Core Competencies
The evaluation requirements of the PISA 2021 Mathematics Literacy Assessment Framework are consistent with the 2022 curriculum standards, both focusing on the achievement of knowledge objectives, the development of cognitive abilities, and the comprehensive attention to students’ core competencies. Research by Professor Yu Ping indicates that since mathematical core competencies stem from mathematical knowledge, the evaluation of core competencies can also begin from a knowledge perspective. He categorizes knowledge learning into three levels: knowledge understanding, knowledge transfer, and knowledge innovation, viewing the three abilities generated from knowledge learning as three levels of core competencies. Based on this theory, we can design advanced problems corresponding to three levels for evaluating core competency levels. In problem design, the problems at the three levels can be arranged in a 7:2:1 ratio, meaning that most children can solve 70% of the basic knowledge understanding level problems, some children can solve 20% of the more difficult knowledge transfer level problems, and a small number of children can take on the challenge of the 10% most difficult knowledge innovation level problems.
Problem 15 (Grade 6)
The area occupied by the sheep pen is a rectangle, 3 meters long and 2 meters wide, with grassland surrounding it. A sheep is tied at the corner outside the sheep pen (as shown in figure 1), and the length of the rope is 2 meters.
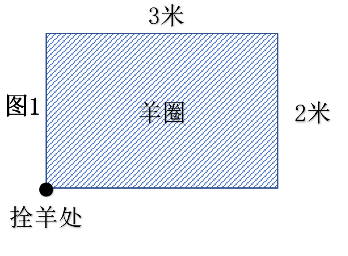
(1) What is the range of grass that the sheep can eat, which means finding what?
(2) Draw the shaded area representing the range of grass the sheep can eat.
(3) Calculate the size of the area of grass the sheep can eat.
(4) If the rope is tied at the midpoint of the long side of the sheep pen (as shown in figure 2), what is the size of the area of grass the sheep can eat?
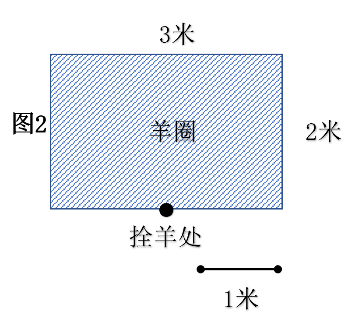
(5) Move the place where the sheep is tied; when can the sheep eat the maximum area of grass? Explain your reasoning.
In Problem 15, parts (1), (2), and (3) belong to level 1 problems, requiring students to use knowledge of circles and calculate the area of circles to establish a model for the sheep’s grazing range. Part (4) is a level 2 problem, where students can transfer knowledge and methods to solve related problems in new contexts. Part (5) is a level 3 problem, where after solving problems 1 and 2, students can flexibly apply knowledge and methods to solve exploratory and open-ended unconventional problems. The design of the three levels of advanced problems achieves an evaluation of the three levels of core competencies.
Since the PISA 2021 Mathematics Literacy Assessment Framework will profoundly impact our basic mathematics education, when designing math problems, we should base them on creating realistic situations, using comprehensive practical applications as a pathway, and employing advanced problem design as a method, focusing on the core of mathematical reasoning, striving to improve students’ problem-solving abilities, thereby realizing the cultivation objectives of core competencies.
[This article was published in the 5th issue of “Primary School Teaching” in 2023, with some omissions]

Author of this article

Wu Weihua, a mathematics researcher at Xiamen Siming District Teacher Training School, an expert mathematics teacher in Xiamen, has been engaged in primary school mathematics teaching for 14 years and has been a mathematics subject researcher for 15 years. His main research focuses are primary school mathematics case studies, classroom observations, and academic evaluations in primary mathematics.

Zhang Chang, a leading primary school mathematics teacher in Xiamen, a senior teacher, and the deputy director of the Academic Affairs Office at Hu Ming Primary School in Siming District, Xiamen. She has won the Xiamen Education System Excellence Award, first prize in the district innovation competition, first prize in the city quality class evaluation, has conducted over thirty public classes and special lectures in provincial, municipal, and district levels, published nine educational papers in CN-level journals, and currently leads a key research project on the “Extraction of Core Issues in Overall Teaching of Primary School Mathematics Units” in Xiamen.

Call for Papers
The “View Exchange” column invites all readers of the “Ming Teacher’s Way” WeChat public account to submit summaries of experiences, papers, and existing confusions and questions related to curriculum standard study, textbook interpretation, and question design research. The editorial team will select excellent submissions for promotion in “View Exchange”. This call for papers is ongoing, and we welcome your participation!

Editor: Fan Qiuxiang
Initial Review: Wei Guocai
Final Review: Lin Jincheng
