Knowledge Group 1: Magnetic Phenomena and Magnetic Fields
1. Magnetic Phenomena and the Magnetic Effect of Electric Current
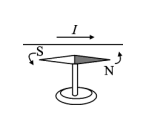
1. Magnetic Phenomena
2. The Magnetic Effect of Electric Current
Knowledge Group 2: Magnetic Induction Intensity and Common Magnetic Fields
1. Magnetic Induction Intensity
1. Direction of Magnetic Induction Intensity
2. Magnitude of Magnetic Induction Intensity


2. Magnetic Field Lines (Key Point)
1. Definition
2. Distribution of Magnetic Field Lines in Common Magnetic Fields
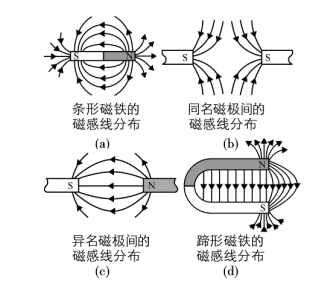
3. Characteristics of Magnetic Field Lines
3. Common Magnetic Fields
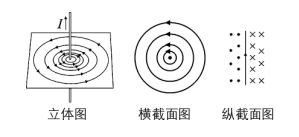
1. Magnetic Field of a Straight Electric Current (Key Point)
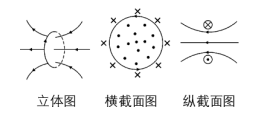
2. Magnetic Field of a Circular Electric Current (Key Point)
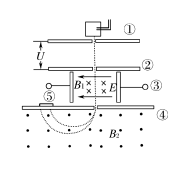
3. Magnetic Field of a Current-Carrying Solenoid (Key Point)
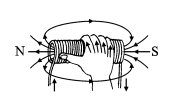
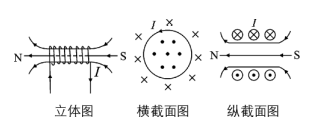
4. Ampere’s Molecular Current Hypothesis
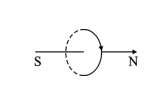
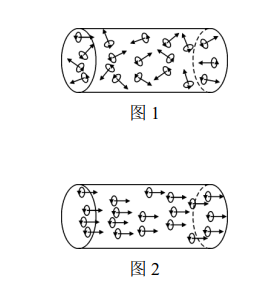
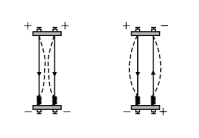
4. Uniform Magnetic Field
1. Definition
2. Characteristics of Magnetic Field Lines
3. Locations of Existence
5. Magnetic Flux
1. Definition
2. Calculation (Key Point)
3. Units

4. Magnetic Flux Density

5. Positive and Negative Magnetic Flux
6. Several Situations of Changing Magnetic Flux
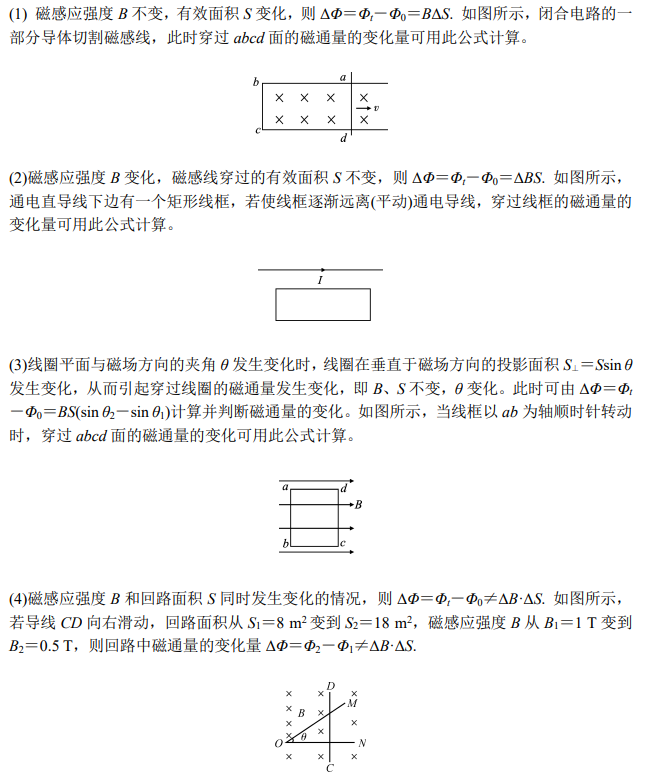
Knowledge Group 3: Ampere’s Force and Lorentz Force
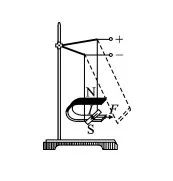
1. Ampere’s Force
1. Ampere’s Force and Its Direction
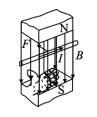
2. Difference Between Ampere’s Rule and Left-Hand Rule
3. Magnitude of Ampere’s Rule (Key Point)

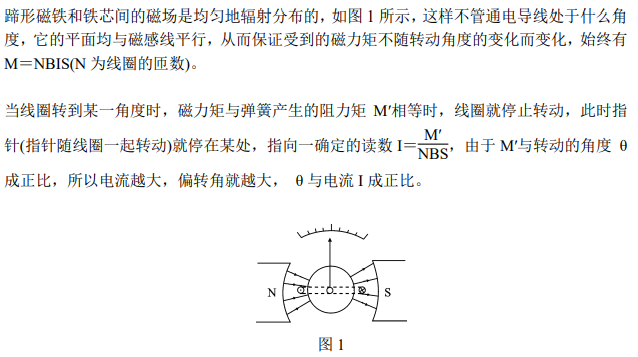
4. The Effect of Uniform Magnetic Field on Current-Carrying Coil
5. Electromagnetic Galvanometer
2. Lorentz Force
1. Magnitude and Direction of Lorentz Force
3. Motion and Application of Charged Particles in Magnetic Fields
1. Motion of Charged Particles in a Uniform Magnetic Field

2. Television Picture Tube

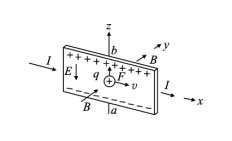
3. Velocity Selector (Key Point)


4. Mass Spectrometer (Key Point)
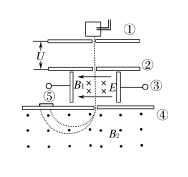
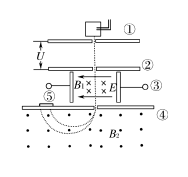
5. Cyclotron (Key Point)

6. Technological Applications of Charged Particles in Magnetic Fields