Understanding the Principles of Bit-Banding Operations in Cortex-M

Bit-banding operations may not be used as much now, but in the past, when MCU performance was not very good, bit-banding operations were a common operation among many software engineers.

This article mainly discusses the Cortex-M3 core (STM32F1), and I believe many friends have been confused when they first learned about it.

1About Bit-Banding Operations

Bit-banding, abbreviated as bit-band, is also known as bit-segment. After supporting bit-banding operations, you can use ordinary load/store instructions to read and write individual bits.

Many friends come from learning the 51 microcontroller and know that the P1.1 pin can be controlled individually; the pin we are operating on is a Bit bit.

We all know that in STM32, you cannot directly operate on a specific Bit of a register, for example, to control the ODR1 in the data output register of the PA port individually, as shown below:

The STM32F1 core Cortex-M3 has long considered this issue. To achieve direct operation on ODR1 like this Bit, a dedicated address area (bit-band alias) was opened up in the core: You can map Bit positions like ODR1 (bit-band area) to the corresponding address in the bit-band alias area, and by operating on the mapped address, you can operate on the ODR1 bit.

In simple terms, this is a mapping operation, but there are many conventions to follow for this mapping operation.

2Mapping Relationships in Bit-Banding Operations

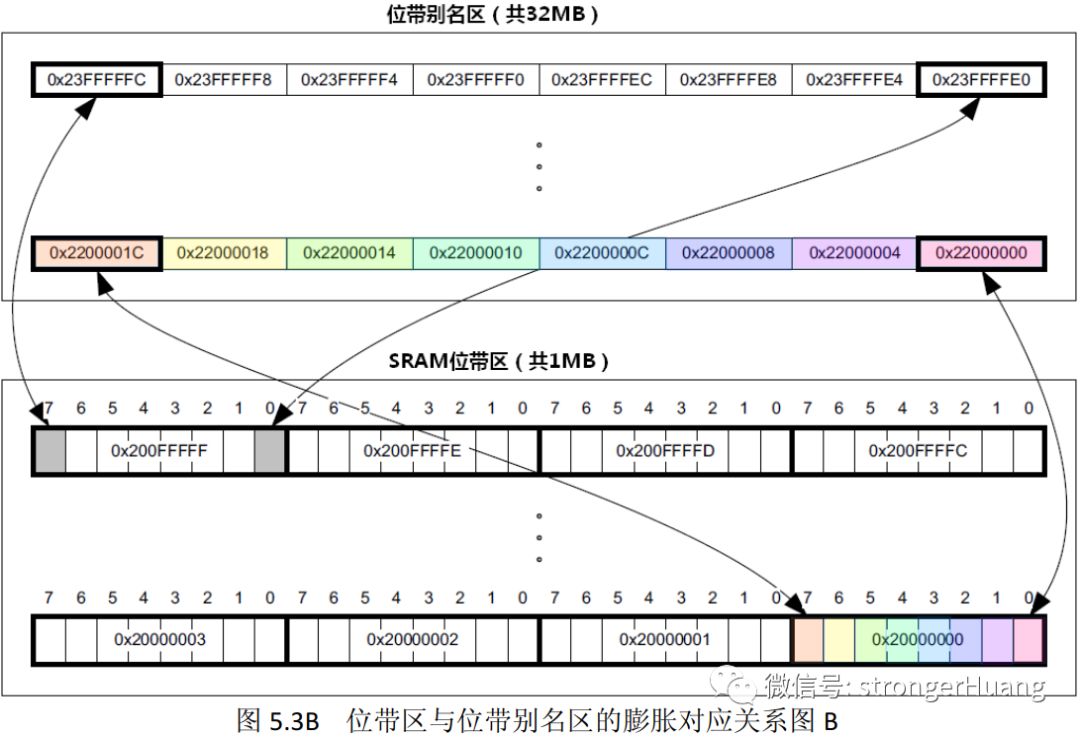
In Cortex-M3, there are two areas that implement bit-banding operations, one is the SRAM area of the lowest 1MB range, and the second is the on-chip peripheral area of the lowest 1MB range.

These two areas are marked in red in the following figure:

These two 1MB will be mapped to another two address areas:

• The lowest 1MB of the SRAM area (0x2000 0000—0x200F FFFF) maps to (0x2200 0000 — 0x23FF FFFF).

• The lowest 1MB of the on-chip peripheral area (0x4000 0000—0x400F FFFF) maps to (0x4200 0000—0x43FF FFFF).

In fact, it is mapped to an offset (distance from itself) of 0x0200 0000 outside the 32MB space (bit-band alias area), as shown in the SRAM area mapping relationship:

Understanding the Principles of Bit-Banding Operations in Cortex-M

Tip: The colored 8Bit in the figure is mapped to an offset 0x0200 0000 outside the 32Bit (4Byte) space.When we read and write the address 0x2200 0000, we are actually operating on the Bit0 of 0x2000 0000.

This is known as the “bit expansion correspondence“, where 1Bit expands to 32Bit (4 bytes).The 4 bytes correspond to the address of that 1Bit, and the data in that address is only valid for the lowest bit (LSB).

Explanation of the keywords that appear multiple times above:

• Bit-band area: The address area that supports bit-banding operations.

• Bit-band alias: Access to the alias address ultimately acts on the access of the bit-band area.

3Bit-band Area to Alias Area Calculation Formula

The main purpose of bit-banding operations: to calculate the alias area address (AliasAddr) from the bit address (A).

1. SRAM Area Calculation Formula

AliasAddr＝0x22000000+((A‐0x20000000)*8+n)*4=0x22000000+(A-0x20000000)*32+n*4

2. On-chip Peripheral Area Calculation Formula

AliasAddr＝0x42000000+((A-0x40000000)*8+n)*4=0x42000000+(A-0x40000000)*32+n*4

Since the mapping relationship is the same, the principle of the formula is also the same; only the addresses are different. The calculation formula needs to be understood in conjunction with the bit expansion correspondence shown in the above figure.

*8: 1 word is 4 bytes

*4: 1 byte is 8 bits

4Code Implementation

Using the above calculation formula, the process of code implementation is very simple; our goal is to perform read and write operations on the “AliasAddr” address.

1. RAM Bit-Banding Operation Macro Definition

#define BITBAND_RAM(RAM, BIT) (*((uint32_t volatile*)(0x22000000u + (((uint32_t)&(RAM) - (uint32_t)0x20000000u)<<5) + (((uint32_t)(BIT))<<2))))

2. Peripheral Register Bit-Banding Macro Definition

#define BITBAND_REG(REG, BIT) (*((uint32_t volatile*)(0x42000000u + (((uint32_t)&(REG) - (uint32_t)0x40000000u)<<5) + (((uint32_t)(BIT))<<2))))

For comparison, here is a screenshot:

A. Write 0 to Bit1 of RAM address 0x20001000

BITBAND_RAM(*(uint32_t *)0x20001000, 1) = 0;

B. Read Bit1 of RAM address 0x20001000

uint8_t Val;Val=BITBAND_RAM(*(uint32_t *)0x20001000, 1);

C. Output 1 to the data output register of PA1

BITBAND_REG(GPIOA->ODR, 1) = 1;

D. Read the data output register of PA1

uint8_t Val;Val=BITBAND_REG(GPIOA->ODR, 1);

Here, we are operating on a specific address, similar to operating on a pointer.

5Advantages and Disadvantages of Bit-Banding Operations

1. Advantages

Compared to directly operating registers, the code is more concise, and the running efficiency is higher. It avoids confusion in multitasking or interrupts.

2. Disadvantages

If operated improperly (incorrect address parameters), it can easily lead to bus faults.

6Conclusion

For more details about the bit-banding operations of Cortex-M3, please refer to the Cortex-M3 Technical Reference Manual (Authoritative Guide).

Later Cortex-M processors no longer support bit-banding operations; from the perspective of compatibility with future software, it is not very recommended for everyone to continue using it.

However, bit-banding operations are a classic; here I share it for everyone to understand, and I hope it helps you.

END

Author: strongerHuang

Source: Embedded Column

Copyright belongs to the original author. If there is infringement, please contact to delete.

▍Recommended Reading

Transitioning from STM32 to Embedded Linux Driver Development

7 Small Websites That Embedded Engineers Can’t Resist (Resource Edition)

ChatGPT Implementing Various Light Control Programs for 51, STM32, Raspberry Pi, etc.

→ Follow to avoid getting lost ←