The RSA encryption algorithm is the cornerstone of modern information security, widely used in network communication, data encryption, and e-commerce. However, with the rapid development of quantum computing, traditional cryptography faces unprecedented challenges. Especially in the era of Noisy Intermediate-Scale Quantum (NISQ) computing, the Variational Quantum Factorization (VQF) algorithm, based on quantum-classical hybrid methods, provides a new approach to breaking RSA. This article will detail the principles of RSA encryption and explore how the VQF algorithm decrypts RSA-encrypted data and its advantages.
01What is the RSA Encryption Algorithm?
The RSA algorithm was proposed in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman as a public key encryption algorithm (RSA is formed from the initials of their last names). RSA is currently the most influential public key encryption algorithm, capable of resisting the vast majority of cryptographic attacks to date, and is recommended by ISO as the standard for public key data encryption.
RSA encrypts and decrypts data using two keys (public key and private key):
• Public Key: A public “lock” that anyone can use to lock (encrypt) information.
• Private Key: A unique “key” for the receiver, which can unlock (decrypt) the “lock”.
For example, if Xiaohong wants to send a love letter to Xiaolu, but there are many intermediaries, Xiaohong does not want the content to be seen by them. Xiaolu provides a box with a lock (the public key, which is analogous to this lock), which can only be opened with Xiaolu’s unique key (the private key, which is analogous to the only key for this lock). After receiving the box, Xiaohong puts the love letter inside and locks it, then hands it to the intermediary. Although the intermediary can access the box and the lock (the public key), they do not have Xiaolu’s unique key (the private key), so they cannot open the box.
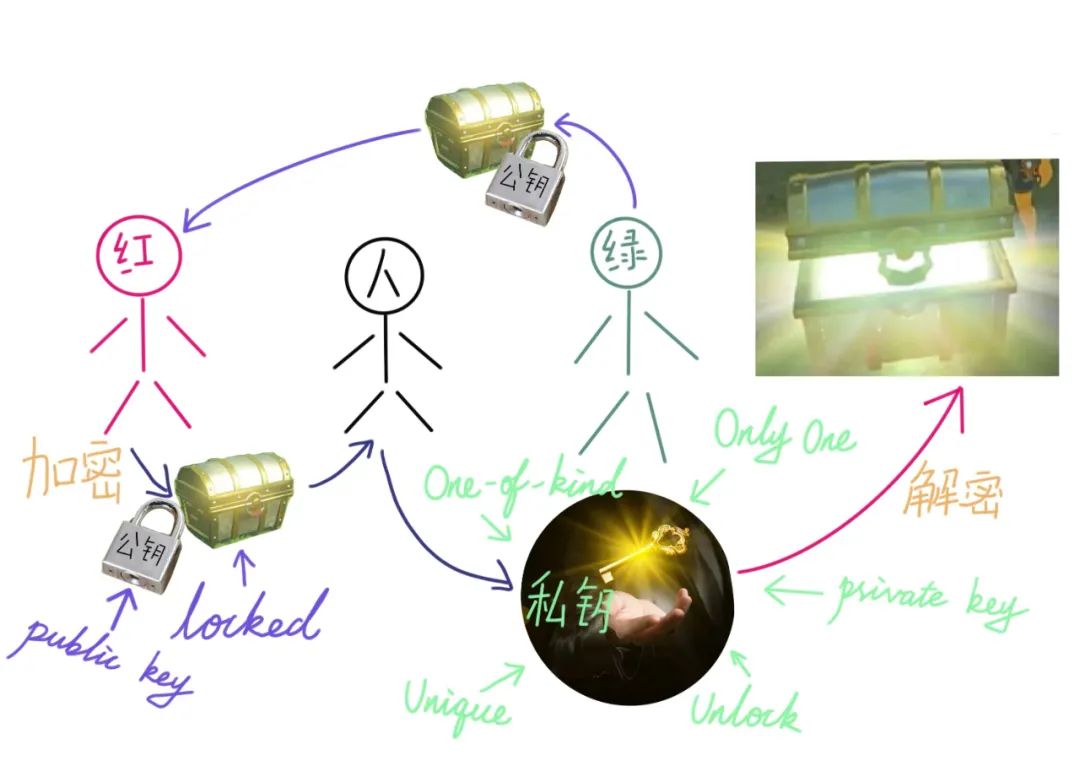
△ Example
However, the security of this encryption relies on the complexity of the lock, which is the difficulty of cracking the private key. If the lock is complex enough, it will be extremely difficult to crack the private key, thus ensuring information security.
02Why is RSA Difficult to Crack?
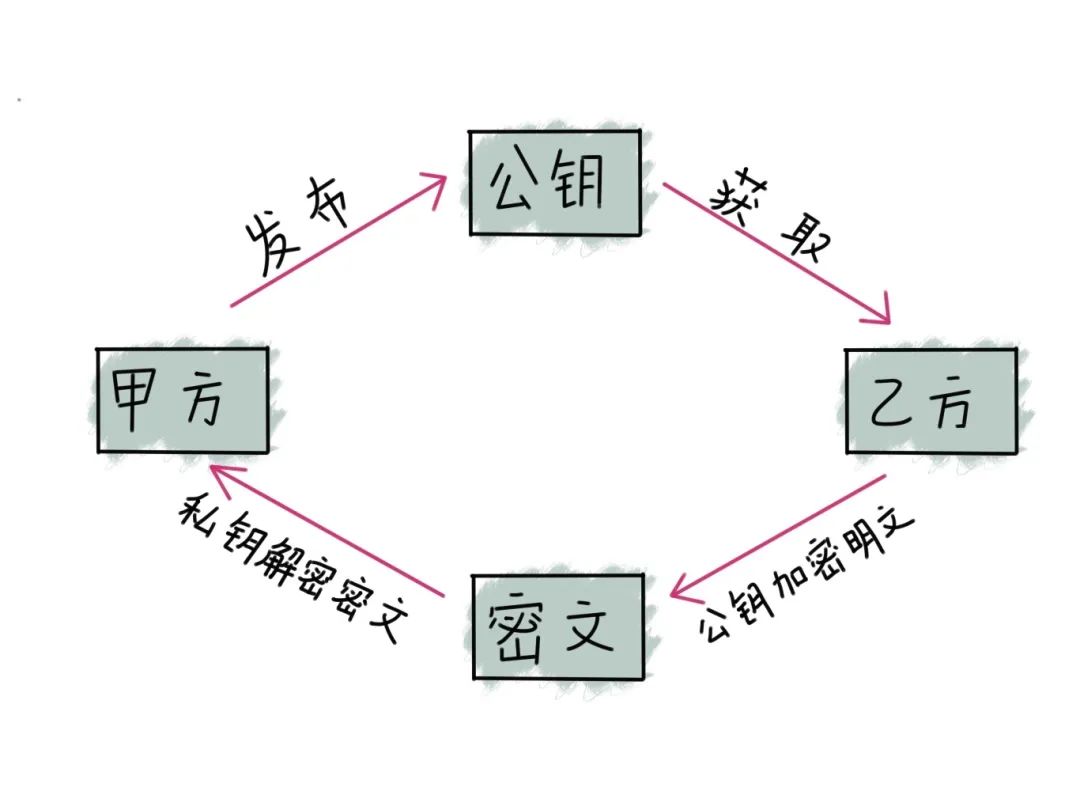
△ RSA Principle
The RSA algorithm is based on a very simple number theory fact: it is easy to multiply two large prime numbers, but extremely difficult to factor their product. Therefore, we publish the product of two large prime numbers as the encryption key.
The core of the RSA algorithm is the factorization problem of large integers N. Specifically, given N=p×q (where p and q are two large prime numbers), cracking RSA requires finding p and q from N, which is a task that is difficult to accomplish in a reasonable time with classical computation.
For example, a 2048-bit RSA key corresponds to an N that typically contains over 600 decimal digits, and factoring such a large integer is impossible to complete in a short time with current classical computing capabilities.
Now, on the China Telecom Quantum “Tianyan” quantum computing cloud platform, you can experience the encryption and decryption process for free. Let us embark on this fascinating journey together to explore the mysteries of quantum technology!
Platform address:https://qc.zdxlz.com/
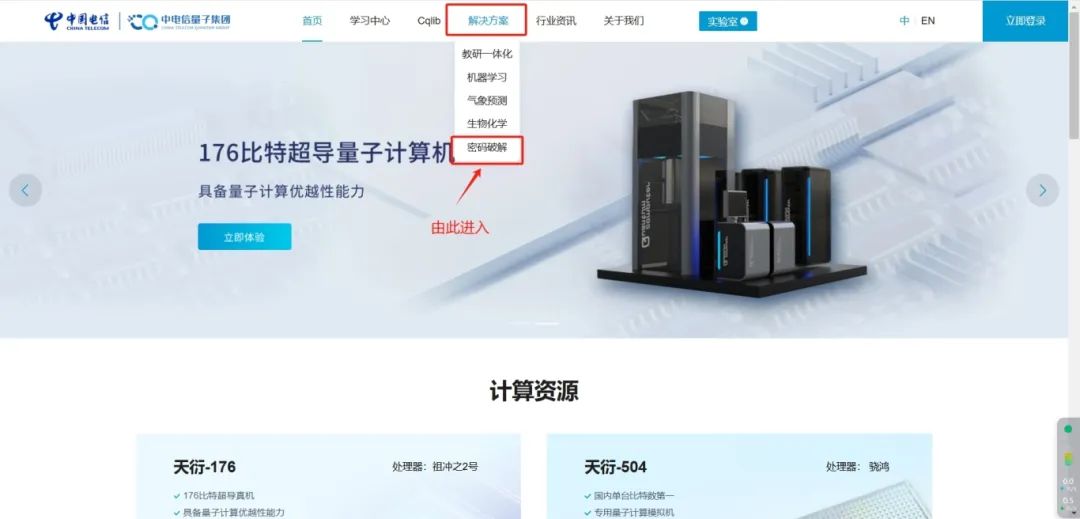
△ Experience Entry
03RSA Encryption Process
The encryption and decryption process of RSA includes the following steps:
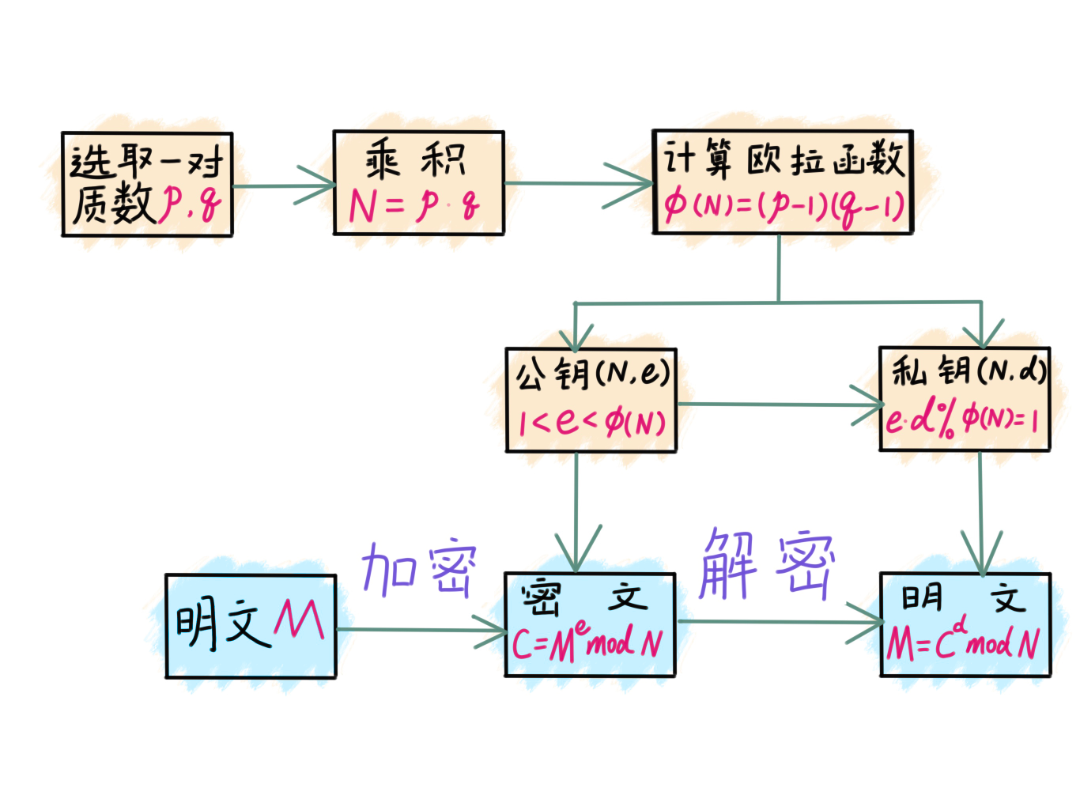
△ RSA Process
01Randomly select a pair of large prime numbers p and q
A prime number is a positive integer that can only be divided by 1 and itself. The larger the selected p and q, the more secure the encryption.
02Calculate the modulus N
N=p×q
For example, if p=97 and q=89, then N=8633. Converting 8699 to binary gives 10000111111011 (14 bits), and the longer the bit length, the harder it is to crack the encryption.
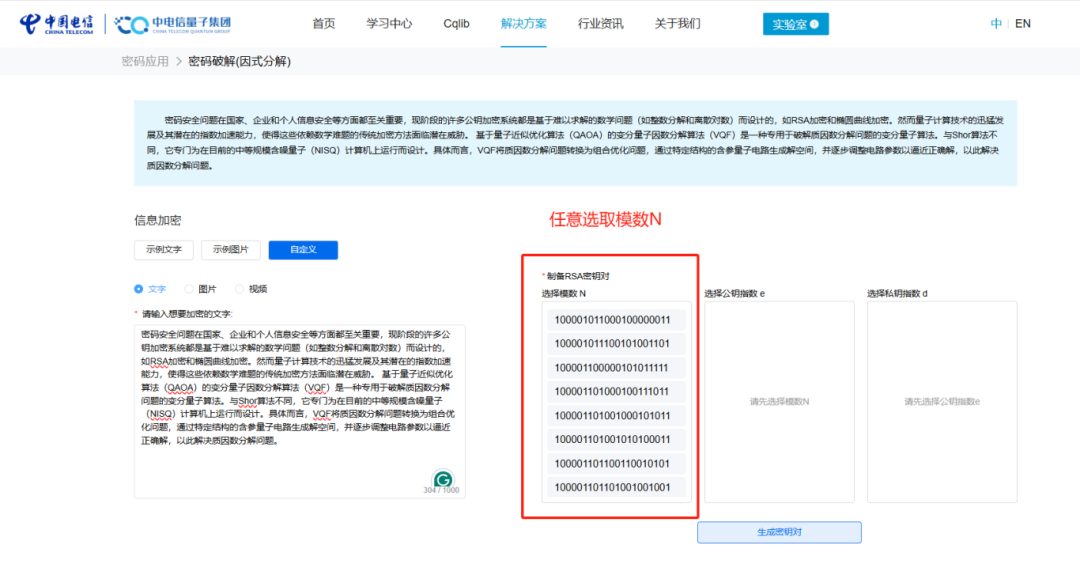
△ Selecting modulus N
03Calculate Euler’s function
Φ(N)=(p-1)(q-1)
Euler’s function represents the count of positive integers less than N that are coprime to N (the only common divisor of the integers is 1). For example, when N=8, the coprime numbers are 1, 3, 5, 7 (where 2, 4, 6 have a common divisor of 2 with 8), thusΦ(8)=4.
04Generate public key e, N
1<e<Φ(N)
e is a random number within the inequality range and is coprime to Φ(N).
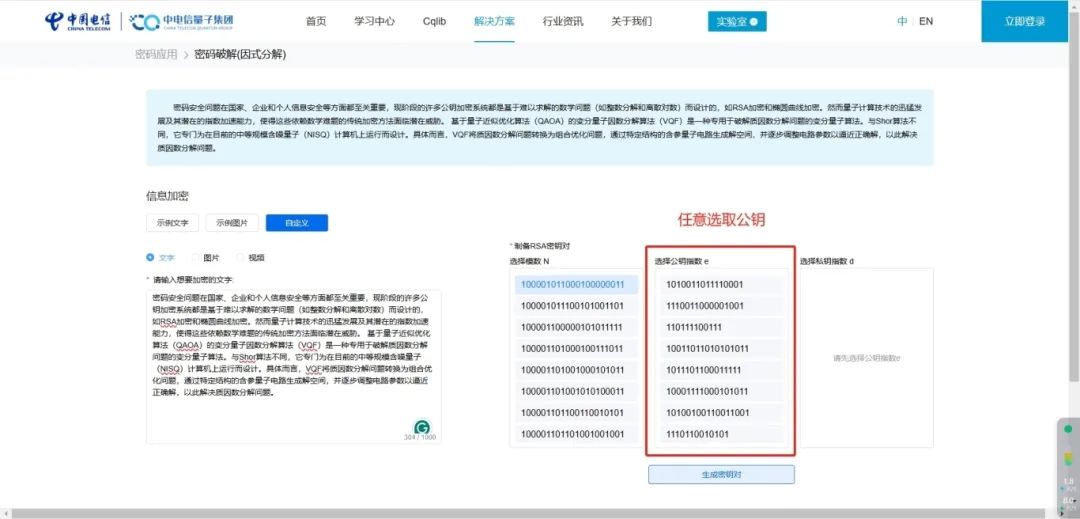
△ Selecting public key e, N
05Generate private key d, N
where d satisfies the following conditions:
• e×d mod Φ(N)=1
Here, d can be solved using the extended Euclidean algorithm.
(The extended Euclidean algorithm is an effective method for solving binary linear equations (such as ax+by=1) by recursively calculating the greatest common divisor to derive d.)
• 1<d<Φ(N)
• d is coprime to Φ
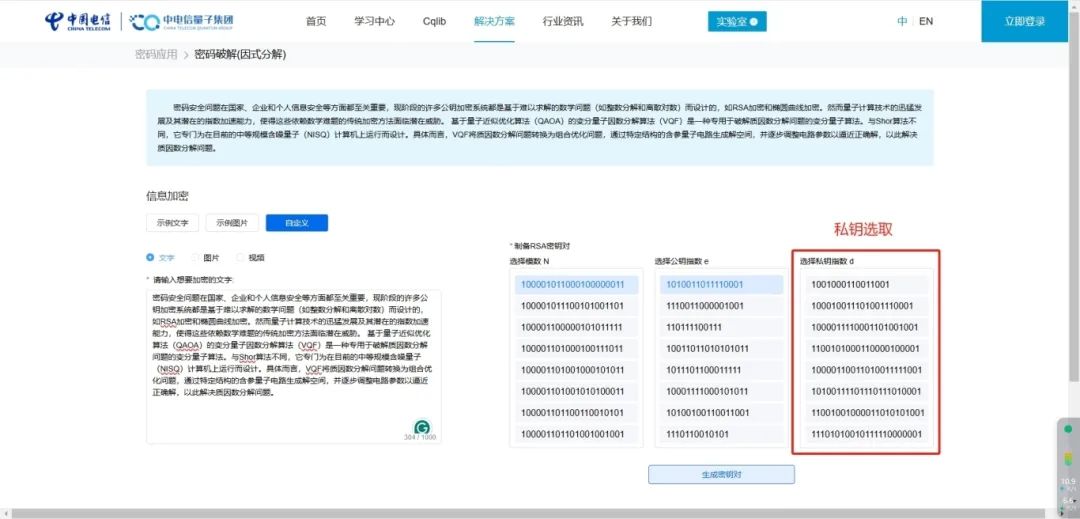
△ Private key selection
06Public key encryption
Encryption formula: C=Me mod N
where M is the plaintext and C is the ciphertext. mod denotes the modulus operation, which calculates the remainder. For example, 9 mod 2=1.

△ Generating ciphertext
04Overview of the VQF Algorithm
VQF is a quantum-classical hybrid algorithm designed to optimize specific objective functions by leveraging the unique advantages of quantum computing (such as ultra-high-dimensional state superposition).
The core idea of this algorithm is to use parameterized quantum states in quantum circuits to represent the solution space of optimization problems, transforming the problem into an iterative process of finding the best parameters. This method combines the powerful computational capabilities of quantum computing with the optimization capabilities of classical computing, aiming to break through the bottlenecks of classical methods.
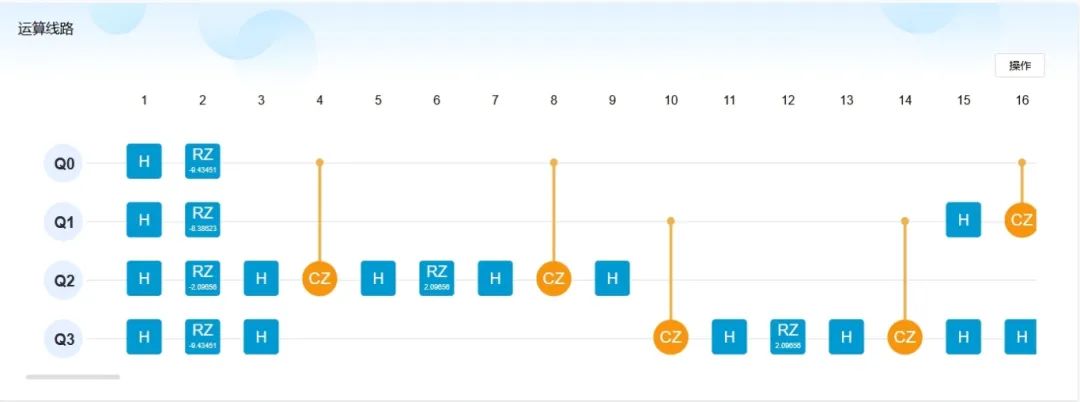
△ For the complete computation circuit, please log in to the “Tianyan” quantum computing cloud platform to view
05Core Steps of the VQF Algorithm01Mathematical Preprocessing: Simplifying Equations
The first step of the VQF algorithm is to reverse the factorization problem N=p*q into a multiplication problem p*q=N; then, based on the multiplication table, transform the multiplication problem into an equation problem; finally, simplify the equation based on the Boolean relationships of each bit to reduce the number of variables (bits).
For example: Factorizing 143=1000 1111 (8-bit binary)
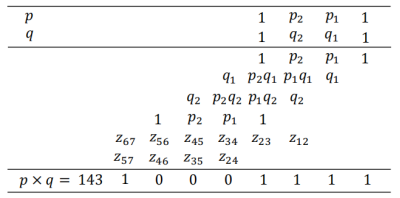
This will transform into a problem of solving equations:
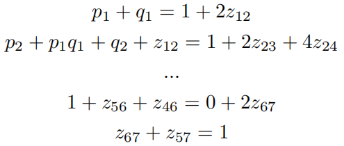
By further simplifying the equation, we aim to reduce the number of unknowns, making it easier to obtain results:
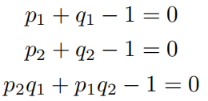
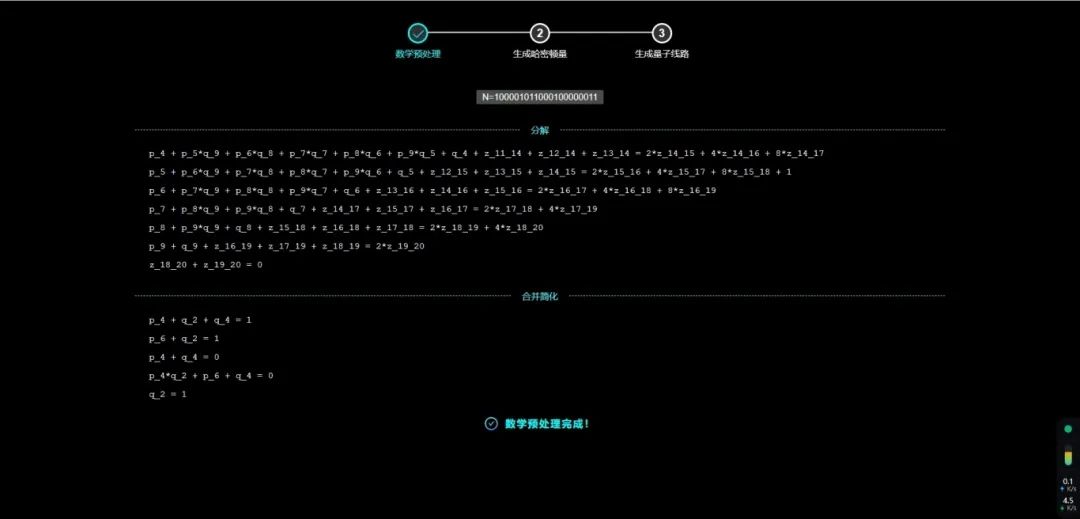
△ Screenshot of the experience process on the Tianyan platform – Mathematical Preprocessing
02Combinatorial Optimization
After preprocessing, the equation-solving problem is transformed into a combinatorial optimization problem.
Using a cost function to optimize parameters:
Cost=(p1+q1-1)2+(p2+q2-1)2+(p2q1+p1q2-1)2
Adjusting the parameters to p1→x0; p2→x1; q1→x2; q2→x3.
Thus, we have: Cost=(x0+x2-1)2+(x1+x3-1)2+(x1x2+x0x3-1)2
03Quantum Problem Transformation
Next, it is necessary to quantize the core computation of the problem on a quantum computer, transforming the combinatorial optimization problem into a Hamiltonian problem suitable for quantum computing.
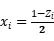
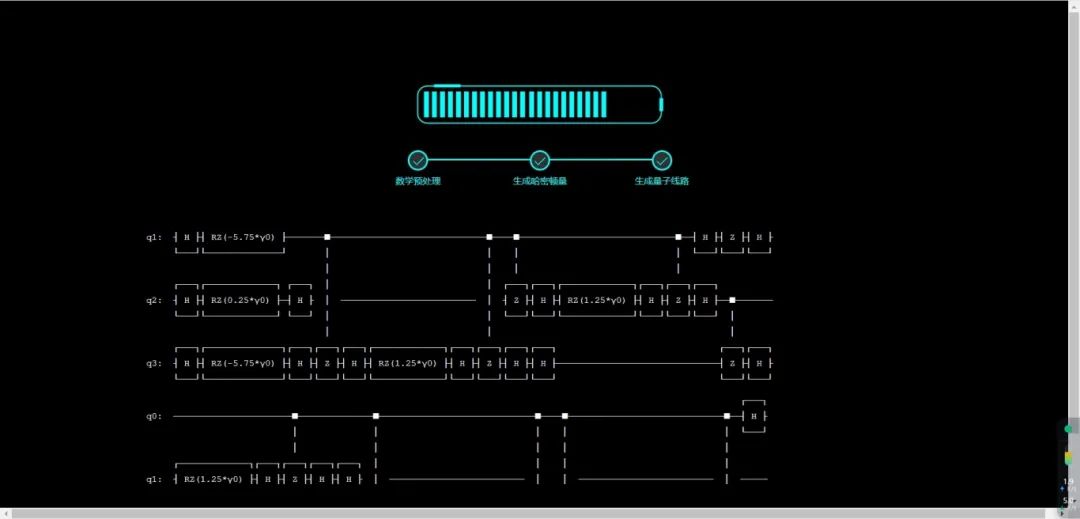
△ Circuit Diagram
04Multiple Iterations: Parameter Optimization Combined with Classical Computation
The essence of the VQF algorithm lies in the collaborative work of classical optimizers and quantum computers, gradually approaching the optimal solution of the problem through multiple iterations while avoiding local minima.
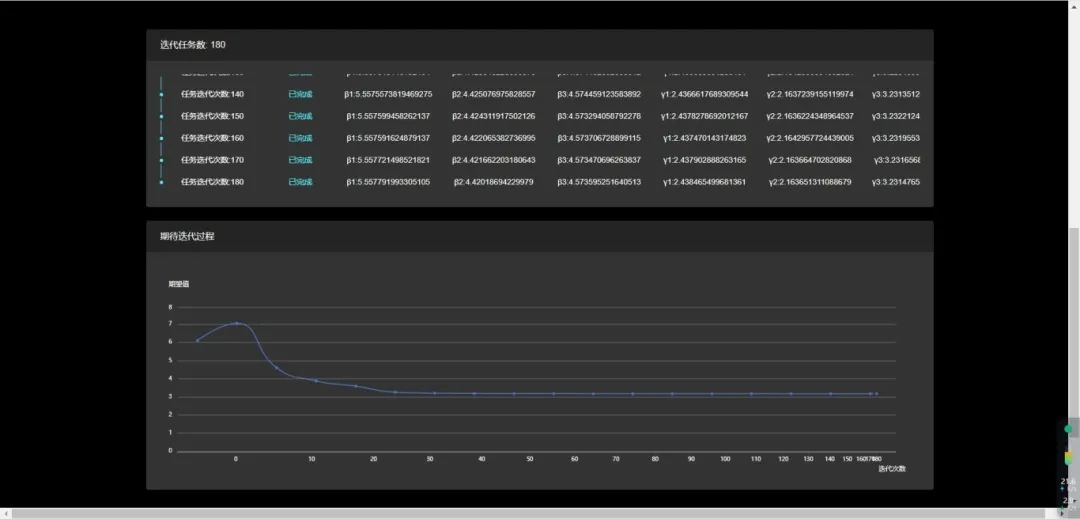
△ Multiple Iterations
05Decoding Results
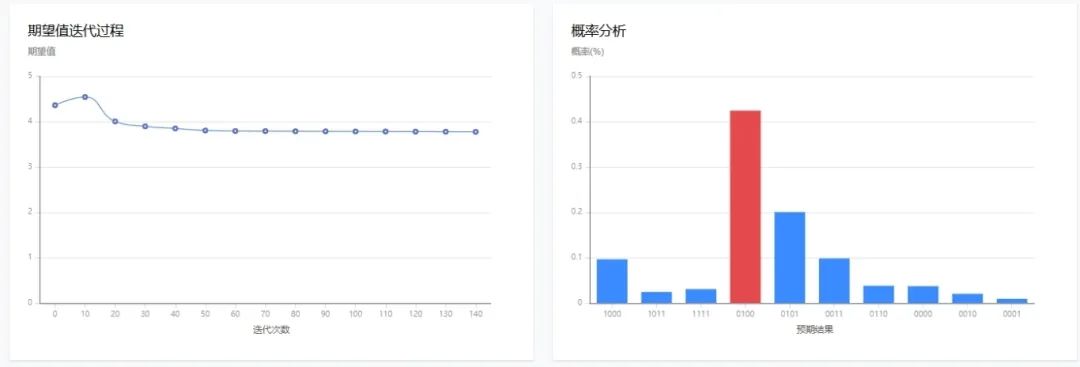
△ Decoding Results
In the result graph, the expected value gradually stabilizes with the number of iterations, indicating that the algorithm is converging during the optimization process, finding the parameter settings that are likely to be optimal or close to optimal. The bars marked in red in the histogram correspond to probabilities significantly higher than other quantum states, indicating that the algorithm successfully concentrated the probability distribution of quantum states on the optimal solution.
Conclusion
The Variational Quantum Factorization (VQF) algorithm accelerates factor search by utilizing the characteristics of quantum superposition and parallel computation, significantly reducing the requirements for the number of qubits and gate depth through the combination of classical optimization. It not only demonstrates the computational potential of quantum algorithms in integer factorization but also indicates that quantum computing remains practically feasible in this field even under hardware constraints, providing technical possibilities for future factorization of larger integers.
To learn more about quantum knowledge
come to the “Tianyan” quantum computing cloud platform!
 Scan or copy the link to access on PChttps://qc.zdxlz.com/
Scan or copy the link to access on PChttps://qc.zdxlz.com/
Authors: Fang Yuhua, Zheng Shuyue
Editor: Liu Lanlan
Executive Editor: Li Jingqing
Reviewer: Ye Bo

More Reading