
High-precision calculation is an algorithm for programming design. Due to the word length limits of the central processing unit, for example, in a 32-bit CPU, an integer can only take a maximum value of 4,294,967,295 (=2^32-1). Therefore, in out-of-range numerical calculations, simulation methods are often required. Typically, the method of separating characters is used to process numerical arrays.
Wikipedia: High-Precision Calculation
In the first two parts, I introduced how to use MATLAB’s built-in toolbox and the toolbox developed by the expert John D’Errico to perform high-precision calculations. This part serves as the finale for high-precision calculations with MATLAB, introducing a high-precision computing tool that is much more efficient than the toolboxes discussed in the previous two parts — Multiprecision Computing Toolbox for MATLAB (AdvanpixMCT).
Before we start, let’s take a look at the official comparison table to see how the AdvanpixMCT tool compares in efficiency with the built-in VPA, Maple, and Mathematica:
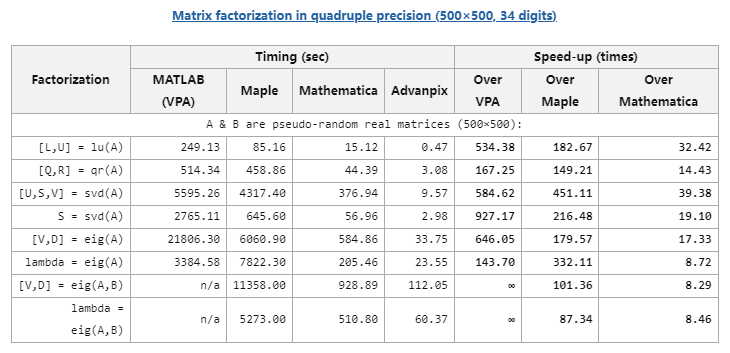
(Screenshot from www.advanpix.com)
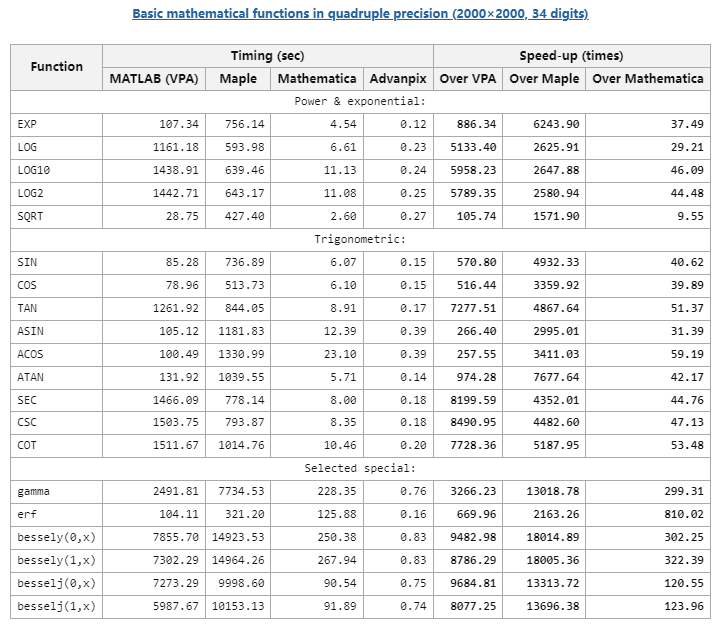
(Screenshot from www.advanpix.com)
From the two tables above, it is clear that whether for matrix calculations or regular calculations, AdvanpixMCT outperforms the other three tools, with computing efficiency far exceeding MATLAB’s VPA and Maple, and significantly leading Mathematica. I think this is also why AdvanpixMCT has become a paid toolbox.
AdvanpixMCT provides computational support covering the following areas:
-
Real and complex numbers, full matrices and sparse matrices, multi-dimensional arrays
-
Elementary and special mathematical functions
-
Solvers for linear equations (including direct and iterative sparse solvers)
-
Matrix analysis functions and factorization
-
Eigenvalues and eigenvectors, including generalized and large-scale problems.
-
Singular value decomposition
-
Solvers for nonlinear equations (using Levenberg-Marquardt and other trust-region methods for fsolve)
-
Numerical integration (including adaptive quadgk and the full set of Gaussian quadrature)
-
Optimization and polynomials
-
Ordinary differential equation solvers
-
Data analysis and Fourier transforms
-
Number theory functions
In the first two parts, I have explained a lot about how to define and use the high-precision calculation toolbox, and the usage of AdvanpixMCT is not much different from them. After installing the free 7-day trial version, you can test using the example code in the following code block.
>> mp.Digits(34); % Setup default precision to 34 decimal digits (quadruple).>> format longG % Toolbox shows all digits in case of 'long' formats.% Simple expressions evaluation in quadruple precision:>> x = mp('pi/4') x = 0.7853981633974483096156608458198757 >> y = mp('sqrt(2)/2')y = 0.707106781186547524400844362104849 >> A = repmat(x,10,10); % Create mp-matrix by scalar replication.>> norm(y-cos(A)) % Calculations are done with 34 digits precision.ans = 9.629649721936179265279889712924637e-35 % Assemble matrix row by row:% (Butcher tableau for Gauss-Legendre method: https://goo.gl/izuFWg)>> a1 = mp('[ 5/36 2/9-sqrt(15)/15 5/36-sqrt(15)/30 ]');>> a2 = mp('[ 5/36+sqrt(15)/24 2/9 5/36-sqrt(15)/24 ]');>> a3 = mp('[ 5/36+sqrt(15)/30 2/9+sqrt(15)/15 5/36 ]');>> a = [a1;a2;a3]; % Concatenate rows into final matrix % Create mp-matrices by conversion from double>> A = mp(rand(5));>> B = mp(eye(5));>> [V,D] = eig(A,B);>> norm(A*V - B*V*D,1)/(norm(A,1) * norm(B,1))ans = 8.1433805952291741154581605524001229e-34 % Create sparse matrix with accumulation using triplets:>> i = [6 6 6 5 10 10 9 9]'; >> j = [1 1 1 2 3 3 10 10]';>> v = mp('[100 202 173 305 410 550 323 121]')'; % Prepare vector of nonzeros>> S = sparse(i,j,v) % Form quadruple precision sparse matrixS = (6,1) 475 (5,2) 305 (10,3) 960 (9,10) 444Is high-precision calculation really that important? In some cases, it is necessary to use high-precision calculations, such as when dealing with ill-conditioned eigenvalue problems. The only reliable way to achieve accurate calculations is to extend the computation precision. Below, let’s take a look at the importance of precision in handling ill-conditioned eigenvalue problems using the examples provided by AdvanpixMCT. We will use the eigenvalue-sensitive Grcar matrix for demonstration. The Grcar matrix contains only -1, 0, and 1 as its elements, and can be generated in MATLAB by calling the gallery function, such as an 8*8 Grcar matrix:
gallery('grcar',8)ans = 1 1 1 1 0 0 0 0 -1 1 1 1 1 0 0 0 0 -1 1 1 1 1 0 0 0 0 -1 1 1 1 1 0 0 0 0 -1 1 1 1 1 0 0 0 0 -1 1 1 1 0 0 0 0 0 -1 1 1 0 0 0 0 0 0 -1 1Theoretically, the Grcar matrix and its transpose should have the same eigenvalues. Below, we will use simple code to demonstrate how a small error can lead to a large discrepancy.
% MATLAB floating-point precisionA = -gallery('grcar',150);figure('Color','w');plot(eig(A),'k.'), hold on, axis equalplot(eig(A'),'ro') % MATLAB VPA high-precision calculation (34 digits precision)digits(34); A = vpa(-gallery('grcar',150));eA = eig(A);cA = eig(A');figure('Color','w');plot(eA,'k.'), hold on, axis equalplot(cA,'ro')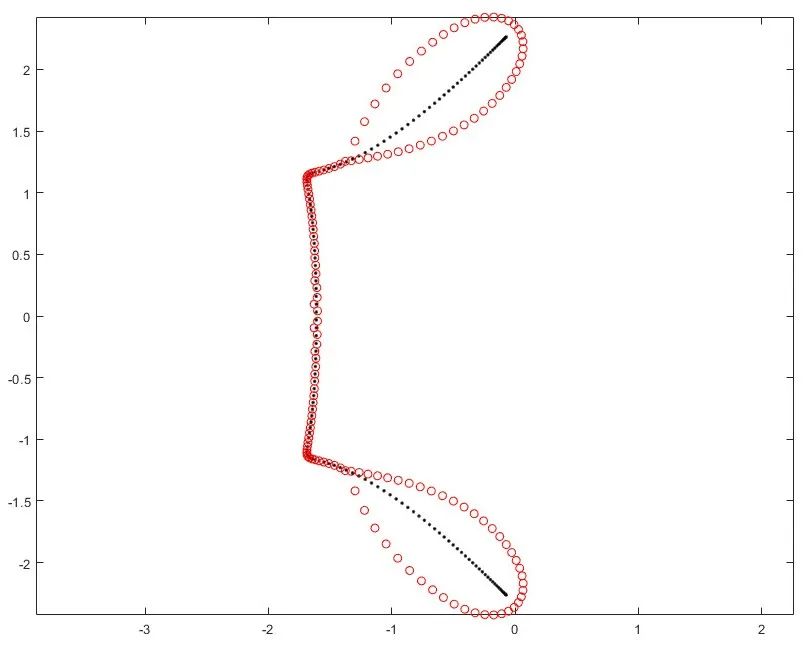
(a) Floating-point calculation results
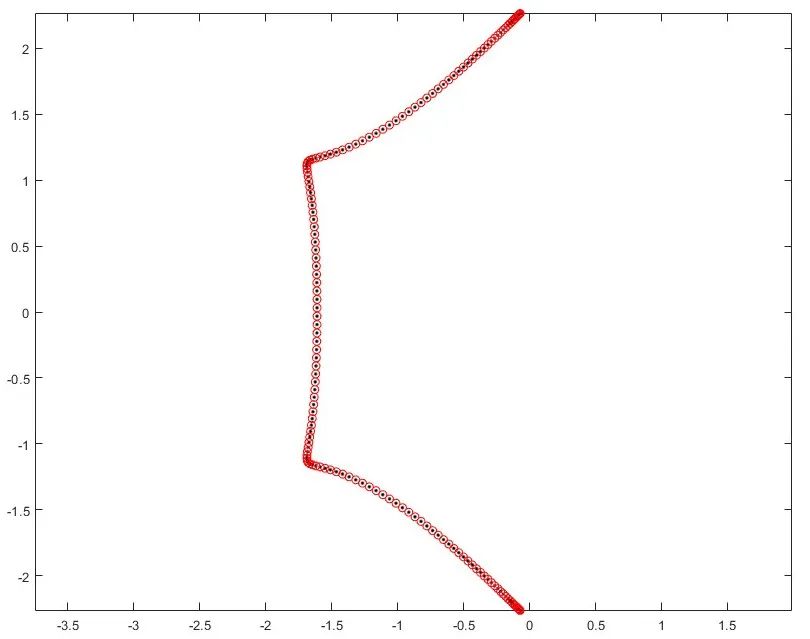
(b) VPA high-precision calculation results
In figures (a) and (b), the black dots represent the eigenvalue plot of the 150*150 Grcar matrix, while the red dots represent the eigenvalue plot of its transpose matrix. Although the condition number cond(A) = cond(A’) = 3.6106 is not high, using double precision floating-point calculations still leads to significant errors.
The basic introduction is coming to an end. Interested partners can further explore more application scenarios based on the help documentation.
As a powerful MATLAB high-precision calculation toolbox, AdvanpixMCT is not cheap, with the academic single-user version priced at $249, and the enterprise single-user version priced at $996. For student users, a 50% discount can be obtained by sending an email. Even at half price, it is still about 830 RMB. I originally wanted to get it, but after thinking about it, I hesitated a bit; with 800 RMB, I could buy an individual license for Endnote 20 (PS: I am already hooked).AdvanpixMCT uses VMProtect strong encryption methods and some special file association methods. After installation, if the 7-day trial period expires, even after uninstalling and reinstalling, it cannot be reused unless the system is reinstalled.
 . Reminder:AdvanpixMCT trial version currently has no functional limitations; all functions are available for trial.
. Reminder:AdvanpixMCT trial version currently has no functional limitations; all functions are available for trial.However, long-term followers of our public account know that we have never encouraged the use of pirated versions. The above method is only a temporary solution; it is better to use the genuine version when you have the ability to support it. I have already gotten the 50% discount code, and if any partners are willing to support me in purchasing AdvanpixMCT, I will exchange it for the qualification to join the original code group, and the appreciation amount will be adjusted to the historical lowest, while providing free AdvanpixMCT computing service support for participating partners. For details, please see the next tweet.
References:www.advanpix.com

For reprints, please reply “Reprint” in the public account to obtain authorization!