C++ Loop Practice Problem – Iterative Method for Square Root Calculation

Time Limit: 2s Memory Limit: 192MB

Problem Description

Calculate the square root using the iterative method

Formula: The iterative formula for finding the square root of a is: X[n+1]=(X[n]+a/X[n])/2. The absolute difference between two consecutive results must be less than 0.00001. Output should be rounded to 3 decimal places.

Input Format

X

Output Format

The square root of X

Sample Input

4

Sample Output

2.000

Code

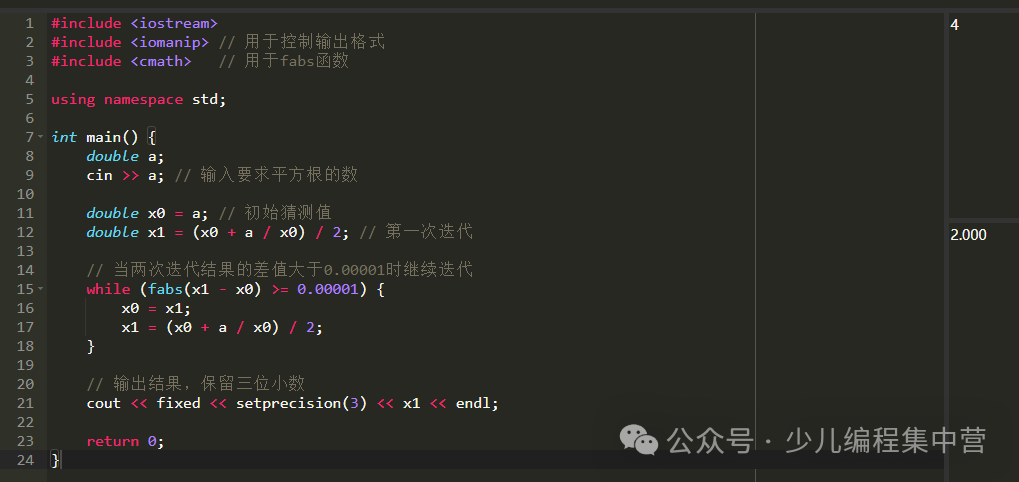
#include <iostream>#include <iomanip> // For controlling output format#include <cmath>   // For fabs function
using namespace std;
int main() {    double a;    cin >> a; // Input the number for which square root is required
    double x0 = a; // Initial guess    double x1 = (x0 + a / x0) / 2; // First iteration
    // Continue iterating while the difference between two results is greater than 0.00001    while (fabs(x1 - x0) >= 0.00001) {        x0 = x1;        x1 = (x0 + a / x0) / 2;    }
    // Output result, rounded to three decimal places    cout << fixed << setprecision(3) << x1 << endl;
    return 0;}

Output Result

Code Explanation

1. (1) Input Handling:

• Use<span>cin</span> to read the user input value a.

(2) Variable Initialization:

• <span> x0</span> is initialized to a (initial guess).

• <span> x1</span> calculates the first iteration result: (x0 + a/x0)/2.

(3) Iterative Calculation:

• Use<span>while</span> loop to continue iterating while the difference between two results is greater than or equal to 0.00001.

• Each iteration updates x0 to the previous x1, then calculates a new x1.

(4) Output Result:

• Use<span>fixed</span> and<span>setprecision(3)</span> to ensure the output is rounded to three decimal places.

Example Demonstration

For the sample input a=4:

1. Initial guess: x0 = 4

2. First iteration: x1 = (4 + 4/4)/2 = 2.5

3. Second iteration: x0 = 2.5 → x1 = (2.5 + 4/2.5)/2 = 2.05

4. Third iteration: x0 = 2.05 → x1 = (2.05 + 4/2.05)/2 ≈ 2.0006

5. Fourth iteration: x0 ≈ 2.0006 → x1 ≈ 2.00000009

6. At this point |x1 – x0| < 0.00001, stop iterating

7. Output 2.000

Mathematical Principle

1. This method is actually a special case of Newton’s iterative method for finding square roots. It converges quickly to the true value of the square root through continuous approximation.

2. Notes

3. 1. The choice of the initial guess is important, usually a itself is chosen as the initial value.

   2. Use<span>fabs</span><span> to calculate the absolute value, ensuring the difference is positive.</span>

   3. The loop condition must be >=, because when the difference is exactly 0.00001, iteration should still continue.

   4. The output format must strictly retain three decimal places.

C++ Basic Tutorial Collection

C++ Basic Materials

1. C++ Output

2. C++ Variables

3. C++ Input

4. C++ Expressions

5. IF Statements

6. IF Applications

7. WHILE Loop Statements

8. FOR Loop Statements

9. Arrays

10. One-Dimensional Arrays

11. Two-Dimensional Arrays

12. C++ Functions

13. C++ File Operations – Writing Files

If you find it useful, please click on me