

Algorithm: The basic ideas and methods for solving problems with computers.
Description of the algorithm: It describes the methods and steps taken to solve a problem or complete a task, including what data is needed (what data is input, what results are output), what structures are used, what statements are employed, and how these statements are arranged. Algorithms are usually described using natural language, structured flowcharts, pseudocode, etc.1. Simple Algorithms for Counting, Summing, and Factorials
These types of problems require loops, and it is important to determine the initial value, end value, or termination condition of the loop based on the problem. It is also essential to pay attention to the initial values of the variables used to represent counts, sums, and factorials.
Example: Use a random function to generate 100 random integers in the range [0, 99], count the occurrences of the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0 in the ones place, and print the results.
This problem is handled using arrays, where the array a[100] stores the generated 100 random integers, and the array x[10] stores the counts of the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. For instance, the count of numbers with 1 in the ones place is stored in x[1], the count of numbers with 2 in the ones place in x[2], and so on, with the count of numbers with 0 in the ones place in x[10].
void main() { int a[101],x[11],i,p; for(i=0;i<=11;i++) x=0; for(i=1;i<=100;i++) { a=rand() % 100; printf("%4d",a); if(i%10==0)printf("\n"); } for(i=1;i<=100;i++) { p="a"%10; if(p==0) p="10"; x[p]=x[p]+1; } for(i=1;i<=10;i++) { p="i"; if(i==10) p="0"; printf("%d,%d\n",p,x); } printf("\n"); }2. Finding the Greatest Common Divisor and Least Common Multiple of Two Integers
Analysis: The algorithm for finding the greatest common divisor (GCD) is based on the idea that (Least Common Multiple = Product of two integers / Greatest Common Divisor).
(1) For known two numbers m and n, with m>n; (2) Divide m by n to get the remainder r; (3) If r=0, then n is the GCD, and the algorithm ends; otherwise, proceed to (4); (4) Set m←n, n←r, and repeat (2).
For example: Find the GCD of m="14" and n=6. m n r
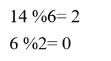
void main() { int nm,r,n,m,t; printf("please input two numbers:\n"); scanf("%d,%d",&m,&n); nm=n*m; if (m<n) { t="n"; n="m"; m="t"; } r=m%n; while (r!=0) { m="n"; n="r"; r="m"%n; } printf("GCD:%d\n",n); printf("LCM:%d\n",nm/n); }3. Checking for Prime Numbers
A number that can only be divided by 1 or itself is called a prime number. The basic idea is to take m as the dividend and use numbers from 2 to INT( ) as divisors. If none divides evenly, m is a prime number; otherwise, it is not. (The following code segment can be used to implement this.)
void main() { int m,i,k; printf("please input a number:\n"); scanf("%d",&m); k=sqrt(m); for(i=2;i<k;i++) if(m%i==0) break; if(i>=k) printf("This number is prime"); else printf("This number is not prime"); }Write it as a function that returns 1 if it is prime, and 0 if it is not.
int prime(int m) { int i,k; k=sqrt(m); for(i=2;i<k;i++) if(m%i==0) return 0; return 1; }4. Verifying Goldbach’s Conjecture
Any even number greater than or equal to 6 can be expressed as the sum of two prime numbers.
The basic idea: Let n be any even number greater than or equal to 6, which can be expressed as n1 and n2. Check if n1 and n2 are both prime; if so, it is a solution. If n1 is not prime, there is no need to check n2. Start with n1=3 and check if both n1 and n2 (where n2=N-n1) are prime. Then increment n1 by 2 and check again until n1=n/2.
Using the above prime function, the program code to verify Goldbach’s conjecture is as follows:
#include "math.h" int prime(int m) { int i,k; k=sqrt(m); for(i=2;i<k;i++) if(m%i==0) break; if(i>=k) return 1; else return 0; } main() { int x,i; printf("please input an even number(>=6):\n"); scanf("%d",&x); if (x<6||x%2!=0) printf("data error!\n"); else for(i=2;i<=x/2;i++) if (prime(i)&&prime(x-i)) { printf("%d+%d\n",i,x-i); printf("Verification successful!"); break; } }5. Sorting Problems
1. Selection Sort (Ascending Order)
The basic idea: 1) For a sequence of n numbers (stored in array a(n)), select the smallest number and swap it with the first number; 2) From the remaining n-1 numbers, select the smallest and swap it with the second number; 3) Repeat this process until the sequence is sorted in ascending order. The program code is as follows:
void main() { int i,j,imin,s,a[10]; printf("\n input 10 numbers:\n"); for(i=0;i<10;i++) scanf("%d",&a); for(i=0;i<9;i++) { imin="i"; for(j=i+1;j<10;j++) if(a[imin]>a[j]) imin="j"; if(i!=imin) {s=a; a=a[imin]; a[imin]=s; } printf("%d\n",a); } }2. Bubble Sort (Ascending Order)
The basic idea: (Compare two adjacent numbers and move the smaller one to the front) 1) For n numbers (stored in array a(n)), the first pass compares each pair of adjacent numbers, moving the smaller one to the front. After n-1 passes, the largest number will have
