Most people in society would agree that among the major disciplines of natural sciences, mathematics and physics are the most authoritative, precise, and beautiful. The experience of authority is not easy to grasp, but as time spent in these fields increases, the understanding deepens. The authority of physics is reflected in the simplicity, effectiveness, and quantitative significance of physical laws. These laws are unshakeable, even when dealing with complex systems and multi-dimensional spacetime structures. Conversely, the appreciation of beauty may vary due to personal sentiment, talent, and experience, making it difficult to define and evaluate.Ising, as a physicist, is somewhat of an imposter, but having worked in the field of condensed matter physics for decades, I ask for the temporary qualification to comment on this subject. This discussion also reflects the elegance of physics.
Among the various branches of physics, the authority of condensed matter physics may be relatively lower. The degree of authority is related to the complexity of the objects that physics deals with. Nevertheless, it still demonstrates sufficient authority and aesthetic appeal. This authority may not be as precise as Newton’s law of gravitation or physical constants, which are often shown with many decimal places, as illustrated in Figure 1(A), but is more reflected in the norms of laws and applicable boundaries (order of magnitude). These laws and boundaries are not easily transcended. The evolution of many situations goes something like this: young physicists are often full of ambition and eager to make their mark, so they frequently become overly excited about “unusual” theoretical or experimental results. However, as time passes and experiences and lessons accumulate, physicists gradually realize that unusual things are usually either wrong or have some ’cause’ behind them. Here, the ’cause’ can be referred to as ‘weird’, often pointing to reasons we do not yet know, do not understand, or overlook due to a lack of knowledge and experience. Once the discrepancies are understood, the next step is to return to the source and restore tranquility to the physicist’s career.
The widely accepted tenets of condensed matter physics and quantum materials are that “energy/energy scale” and “symmetry” govern everything. Figure 1(B) shows the typical energy scales of condensed matter physics effects organized by physicists from different perspectives, while the corresponding detection methods are summarized in Figure 1(C).
Such claims may seem arbitrary, but they carry their own connotations.Ising will boldly make a few statements.
(1) The occurrence of physical effects is primarily determined by thermodynamic processes. However, whether the effects can be manifested and utilized by physicists depends on their energy scale. The term “energy scale” refers to the energy change corresponding to the occurrence of the effect, generally indicating the magnitude of free energy decrease. The sayings “the strong eat the weak” and “those who follow will prosper, those who oppose will perish” illustrate this principle. The energy of a system is the algebraic sum of the energy scales corresponding to various processes. Only the effect with the largest energy scale is the one that is most easily observed. The meaning of “those who oppose will perish” is that if two effects have opposing energy scales, they compete, leading to one annihilating the other, with the effect of smaller energy scale usually suppressed by that of larger energy scale.
This physical logic has become fundamental knowledge that even high school students encounter. Physicists have long accepted and internalized it. Of course, accepting this knowledge is one thing, and being able to apply it is another. This application is reflected in two aspects: firstly, whether one is accustomed to having a clear estimate of the energy scales of various effects related to physical problems; secondly, whether one can reasonably conduct Hamiltonian modeling or experimental design to simplify the complex to get concise physics. FromIsing‘s experiences, young scholars in theoretical condensed matter are generally aware of this authority. However, the attention given to this authority gradually decreases from experimental condensed matter physicists to materials physicists and chemists. The level of attention affects the control, refinement ability, and research efficiency of scientific problems. Higher attention makes it relatively easier to avoid mistakes, misunderstandings, and confusion. However, the downside that comes with this is the risk of losing some original opportunities due to “cognitive darkness”. Clearly, the recognition of energy scale is a double-edged sword that requires a certain level of literacy and regular examination to avoid missing opportunities while maintaining high exploration efficiency. Readers may benefit from carefully examining the connotations of Figure 1.
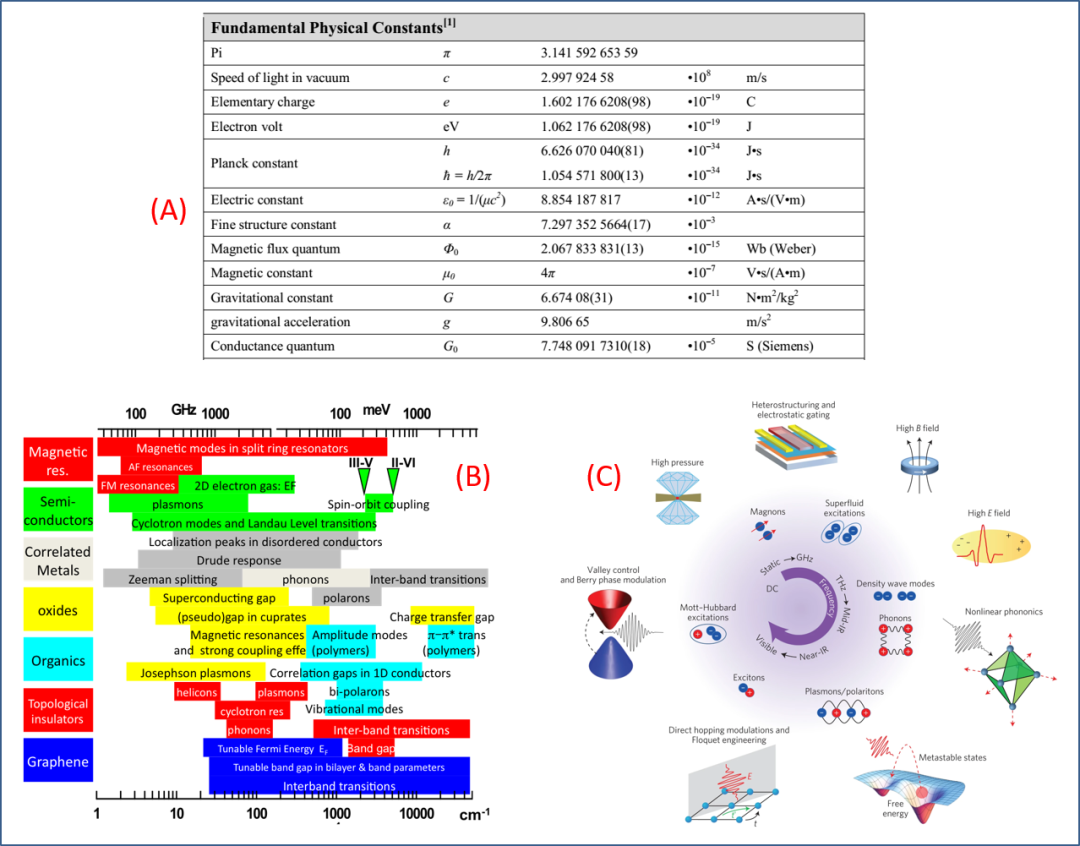
Figure 1. The energy scales and corresponding physical effects of physics and quantum materials as perceived by physicists likeIsing, including detection methods. (A) Several fundamental physical constants, focusing on the effective digits after the decimal point of these constants. (B) The energy scales of some typical effects in quantum materials, indicated by spectral frequency (Hz) and wave number (cm-1). (C) Some spectroscopic measurement methods corresponding to each fundamental physical effect, including the most powerful angular-resolved photoemission spectroscopy ARPES.
(A) Fundamental physical constants, from http://www.scitk.org/subsides/Natural_Science/Physics/Fundamental_Physical_Constants/fund_phys.php.(B) Energy scales of collective excitations in several groups of quantum materials, from Bosov Lab., http://infrared.ucsd.edu/research.html.(C) Methods for controlling quantum phases, and elementary excitations in quantum materials and select control techniques, from D. N. Bosov et al, Nature Mater. 16, 1077 (2017), https://www.nature.com/articles/nmat5017.
(2) The awareness of this authority becomes even more critical and sensitive in quantum materials. Figures 1(B) and 1(C) reiterate this point. Compared to traditional structural materials and smart materials involving light/electric/magnetic effects, the physical effects of quantum materials are much smaller in energy scale. In the realm of physical ensembles, there are fewer large energy scale effects, while the number of small energy scale effects increases rapidly. As the energy scale decreases, two consequences arise: on one hand, smaller energy scales make observation of effects more stringent and require precise control; otherwise, it is difficult to capture them. On the other hand, smaller energy scales lead to a larger number of participating effects, making their competition and coexistence complex and multi-dimensional. Nevertheless, physicists, having experienced countless moments, firmly believe that the dominance of energy scales remains unshakable. The dominance of large energy scale effects and their consistently successful application outcomes give physicists the courage and ambition to challenge the authority of energy scales to achieve extraordinary knowledge.Ising, in ignorance, will provide a few random examples.
The first example is room-temperature superconductivity. If one still believes that superconductivity is the Bose-Einstein condensation of Cooper pairs, the effects determining the superconducting temperature are either electron-phonon coupling or the currently debated spin fluctuation pairing. The energy scale boundaries of these two effects are not difficult to estimate. The energy scale of electron-phonon coupling does not typically exceed the order of ~10 meV (as shown in Figure 2(A) which provides data for some common semiconductors), hence the existence of ceilings like the McMillan limit for superconductivity. The energy scale of spin fluctuations is likely similar, thus the highest superconducting transition temperature is around ~100 K. Coupled with other limiting factors, achieving room-temperature superconducting transition temperature remains a difficult challenge to the authority of physics. Looking back at the recent widely discussed and controversial room-temperature superconductivity data, the skepticism among physicists is not without reason.
The second example is spin-orbit coupling (SOC). Besides the commonly recognized SOC physics, which is the coupling between the spin degree of freedom of outer electrons in the nucleus and its orbital degree of freedom, as shown in Figure 2(B), there are at least two types of SOC effects that significantly impact quantum materials: one is the Dzyaloshinsky-Moriya interaction (DMI), which is a small energy scale effect added to the Hamiltonian of the spin system; the other is the Rashba effect associated with specific symmetry breaking. Of course, since SOC is a universal effect, it can theoretically couple with all other effects in solid-state physics, leading to many physical phenomena derived from SOC. The literature contains many varied and mixed names associated with SOC, andIsing, lacking knowledge, will not elaborate further.
It is reasonable to expect that all higher-order effects derived from the coupling of SOC with other first-order effects cannot exceed the strength of SOC itself. The strength of SOC is directly determined by the atomic number, a fundamental physical quantity. No matter how high the order of coupling, its energy scale cannot exceed that of first-order effects, remaining a smaller energy scale effect. Currently, even for 5d transition metal compounds, the largest SOC energy scale is unlikely to exceed ~10 meV.
The third example could be two-dimensional magnetism and two-dimensional ferroelectricity. The isotropic Heisenberg spin system has long been determined by the MW theorem to be identity-less, meaning it cannot have long-range order. This understanding has reinforced the authority of physics for a long time (which is indeed the case), but it has also somewhat hindered physicists from attempting to explore. Later, due to the magnetic crystal anisotropy brought by two-dimensional crystal structures, spins are no longer purely Heisenberg-type, and finite temperature magnetic order has finally received theoretical and experimental support. Here, it is important to note that whether it is SOC or the so-called spin-lattice coupling, the energy scales remain significant. If one also considers negative contributions from symmetry, and the even smaller interlayer coupling in the out-of-plane direction (as illustrated in Figure 2(C)), the path to enhancing the two-dimensional ferromagnetic temperature and magnetic moment is fraught with challenges.
Two-dimensional ferroelectricity is even more complex. The depolarization field acts like a curse, firmly suppressing the attempt to form sufficiently large out-of-plane spontaneous polarization in two-dimensional ferroelectric materials. Under certain symmetry conditions, out-of-plane polarization can certainly be non-zero, but with the negative effects of two-dimensional fluctuations, even if there is out-of-plane ferroelectricity, its Curie temperature cannot reach that of three-dimensional perovskite oxides. This disappointment and pessimism persisted until several experimental teams in the United States, led by Wu Menghao and his students, managed to realize the concept of “sliding ferroelectricity” in 2016, turning the tide. Now, at least the physics of bilayer two-dimensional ferroelectrics can be looked forward to for some applications. However, Wu Menghao discusses the interlayer physics of bilayer and multilayer vdW systems, similar to magic-angle two-dimensional materials, which is a new branch.
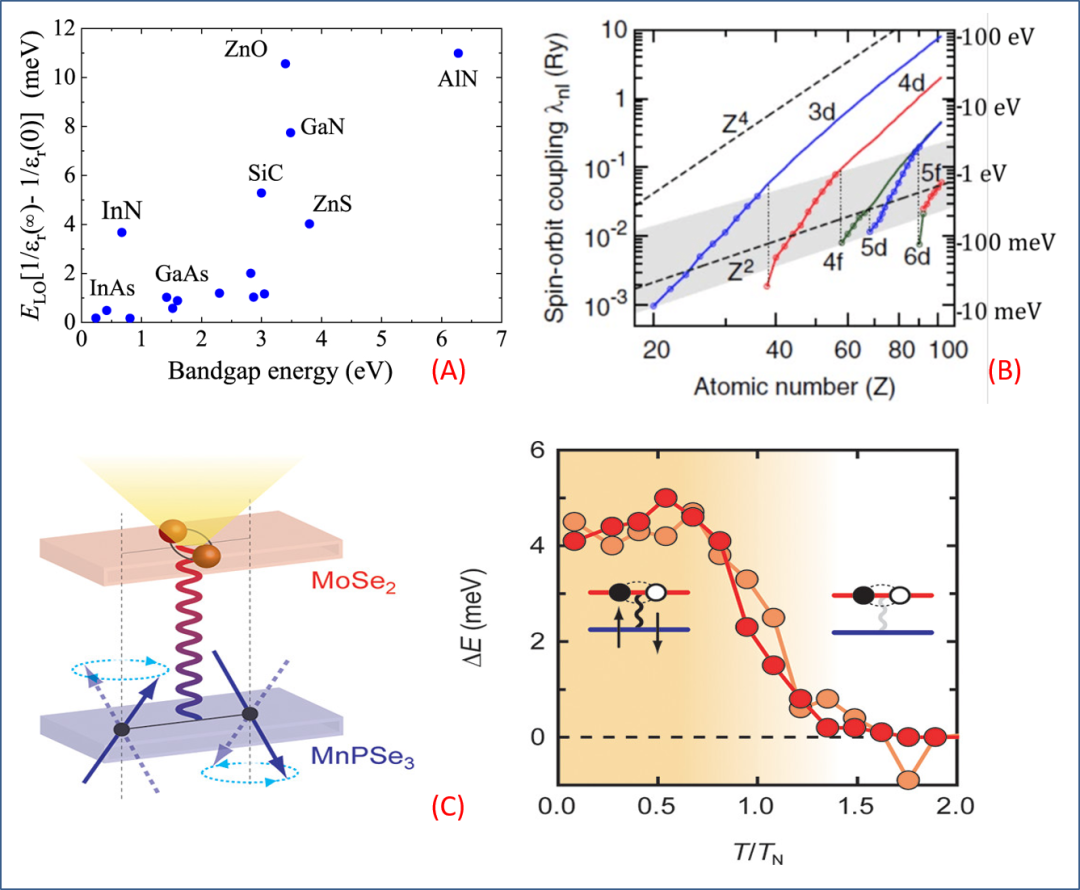
Figure 2. The energy or intensity of some typical effects in quantum materials is roughly illustrated. (A) The relationship between the electron-phonon coupling strength and bandgap for various semiconductors (in fact, not much relationship), noting that most semiconductors have a coupling strength of only ~meV. (B) The dependence of the strength of SOC for different groups of atoms in the periodic table on atomic number. For multielement quantum material compounds, the coupling strength generally decreases by 1 to 2 orders of magnitude, i.e., ~10 meV. (C) The out-of-plane antiferromagnetic coupling energy of typical vdW two-dimensional materials and antiferromagnetic two-dimensional materials can be roughly calibrated by ΔE, which is below ~5 meV.
(A) Electron-phonon coupling strength for various semiconductors, from Y. Ishitani et al, JJAP 58, SCCB34, https://iopscience.iop.org/article/10.7567/1347-4065/ab09e2.(B) Spin-orbital coupling strength, from K. V. Shanavas et al, PRB 90, 165108 (2014), from https://journals.aps.org/prb/abstract/10.1103/PhysRevB.90.165108; F. Hellman et al, RMP 89, 025006 (2017), https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.89.025006.(C) Peak energy shifts of MoSe2/MnPSe3 samples due to antiferromagnetic ordering, where ΔE is the difference between the peak shifts of MPSe3 and that of SiO2 at each temperature, From M. Onga et al, Nano Lett. 20, 4625 (2020), https://pubs.acs.org/doi/10.1021/acs.nanolett.0c01493.
Thus, these three examples, which appear unusual but are actually quite representative, illustrate that physicists understand: in the family of quantum materials with small energy scales and numerous effects, the authority of condensed matter physics still regulates the steps and journeys of physicists chasing their dreams through energy scale. Particularly, as mentioned earlier, the coexistence, competition, and coupling of many small energy scale effects present significant difficulties in describing physical problems, even qualitatively. At this point, grasping the energy scale and using it as a research handle may not be an easy path, worthy of consideration by young scholars.
Having written this far,Ising has piled up a lot of nonsense about energy scales, all of which merely repeats the common knowledge of physicists. Furthermore, one must not forget the authority of “symmetry”. Quantum materials are undoubtedly the discipline that most venerates symmetry, and the physics under symmetry constraints can be accurately presented here. However, the laws of symmetry and its breaking are the premise, conditions, and norms for exploring problems, thus they are not the most difficult issues to handle. For a given system, symmetry determines whether a certain effect exists, which directly determines whether physicists will continue to move forward; this is straightforward and quickly accomplished. If symmetry permits (for example, time-reversal symmetry breaking determines magnetism), then whether the concerned effect can genuinely occur and its magnitude depend on the authority of energy scale, which relies on the coexistence, coupling, and competition of various effects, making the problem complex and turbulent at times. Here, I will mainly focus on “energy scale”; the role of “symmetry” will only be slightly embellished when necessary.
Since the main concern of quantum materials is the effects with small energy scales, the common pursuit faced by the entire field must be how to enhance the intensity of effects and how to increase the temperature at which effects survive for application needs. This common challenge also highlights the achievements of those who have made significant progress in enhancing intensity and increasing temperature. However, at this moment, (1) it is essential to keep in mind the authority of energy scales, as it is not easily challenged; if the effect indicators increase or rise too much, it appears unusual; (2) it is necessary to cautiously consider the authenticity and reliability of experimental findings or theoretical predictions, as the results may stem from errors, fluctuations, or impurity factors; (3) it is crucial to deeply contemplate whether there are other new physical effects or mechanisms that have not been considered, thus reducing the correctness of result interpretations. The interpretation of obtained results depends on a profound understanding of the problem; only by focusing on these three needs can physicists see through effects to mechanisms, through complexity to structure, and through surface to essence.
Setting aside the “false” results caused by computational or measurement errors, for those results that significantly enhance a certain physical effect in an “unusual” manner, one must first consider whether they stem from a lack of interpretation of the results? Are there mechanisms that have not been fully considered? Are there new couplings that have not been recognized? Therefore, excluding non-physical factors and revealing the opportunities behind cognition is the core goal of quantum materials research. The idea that unusual phenomena often have ‘weird’ causes is probably the meaning behind this.
Here, I present a good example that showcases this logical thinking.
In the broad field of quantum materials, the themes of correlated quantum and topological quantum are at the forefront. Both depend on the size and pattern of the SOC in the system. In fact, SOC is the core mechanism behind many new effects in quantum materials, including:(1) New effects related to SOC, such as the quantum Hall effect, new topological states, Berry phase, unconventional superconductivity, and even real-space spin or ferroelectric topological structures, multiferroics, two-dimensional quantum states, all are scenarios where SOC plays a crucial role.(2) Exploring which systems have large intrinsic SOC? In particular, which systems have significant DMI, Rashba effects, etc.? (3) Exploring which specific low-dimensional structures and what types of symmetry-breaking surfaces and interfaces can induce strong SOC? Especially strong Rashba effects? (4) How to utilize strong SOC to construct new topological, correlated, and low-dimensional quantum states? Of course, these topics thatIsing casually mentions do not necessarily represent the mainstream of quantum materials; they merely illustrate that SOC physics is multidimensional and rich.
As previously mentioned, the strength of SOC essentially stems from the intrinsic properties of the atoms that compose the material. However, such intrinsic properties become overall properties related to crystal structure, symmetry, and atomic bonding once these atoms participate in forming a solid lattice. Although the constituent atoms are similar, the overall strength of SOC in different materials significantly depends on the specific structure of the materials. For example, the difference between the electronegativity of a certain atom and that of surrounding atoms has a significant impact on the strength of SOC. Given the complexity of the composition and structure of quantum materials, the SOC of a specific material may become a physical quantity that cannot be precisely predicted. For this reason, researchers in quantum materials are eager to explore whether there exist materials with enormous SOC.
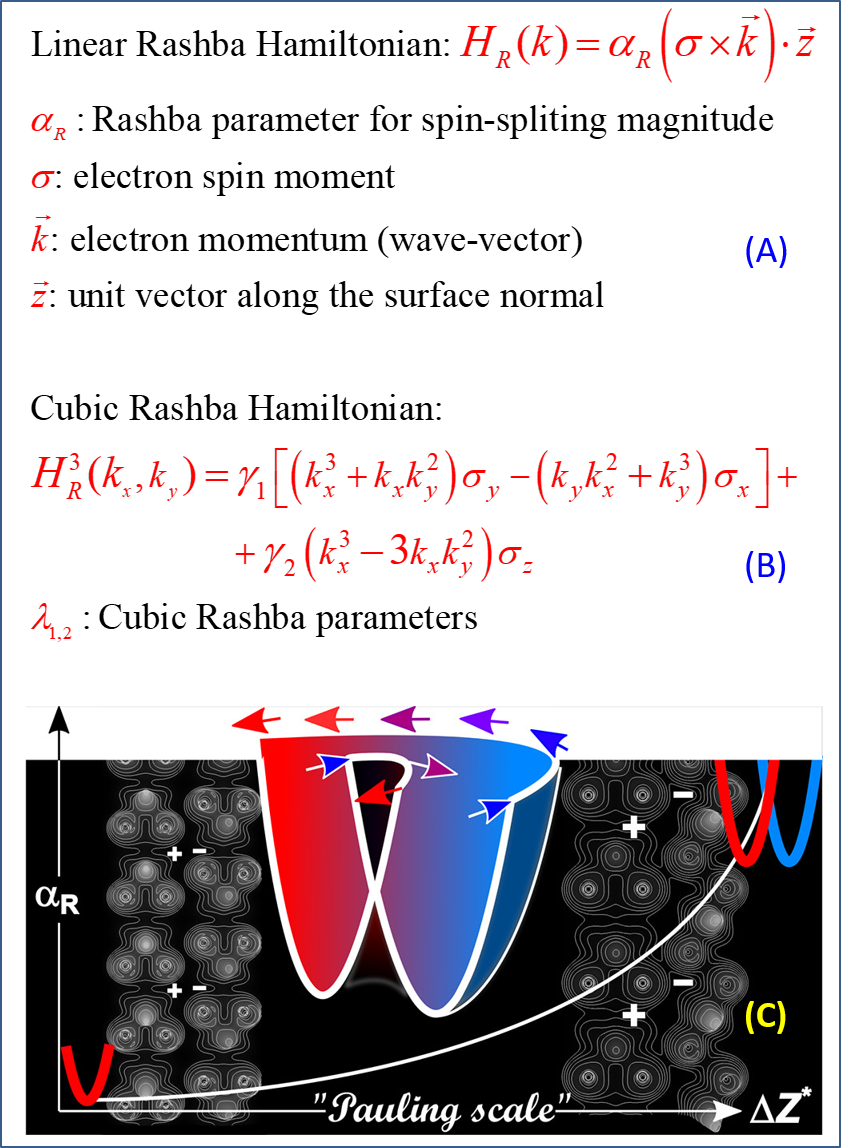
Figure 3. A simplified statement of the Rashba effect in quantum materials. (A) The Rashba effect at the surface of an isotropic system, where αR is the linear Rashba splitting factor, measuring the strength of the spin splitting effect caused by SOC. General experimental measurements and characterizations are based on this expression to calculate αR. (B) The Hamiltonian term considering cubic Rashba splitting effects, where the cubic Rashba splitting factors are γ1,2. (C) The relationship between the linear Rashba factor αR and the Pauling scale electronegativity factor ΔZ*, which has approximately linear dependence on atomic number.from Rashba splitting due to the SOC effect, from S. Gupta et al, JACS 143, 3503 (2021), https://pubs.acs.org/doi/full/10.1021/jacs.0c12809.
However, followingIsing‘s conservative old-fashioned experience, the energy scale of SOC is fixed; it is not an effect that can be easily surpassed. If a computational prediction or experimental discovery suddenly reveals a seemingly ordinary solid with an “unusual” SOC effect, such a determination requires careful analysis. A recently noted example is the observation of a class of non-centrosymmetric narrow bandgap semiconductor compounds with significant Rashba spin-splitting effects (giant Rashba-type spin-splitting). The splitting here manifests as the SOC-induced locking of spins near the Fermi surface. This effect, if understood according to the normal linear Rashba effect, can be measured using the spin-splitting factor αR defined in Figure 3(A). Physicists have long established the relationship between this splitting factor and the so-called Pauling scale (Pauling scale), as shown in Figure 3(C). The Pauling scale is a measure of atomic electronegativity that depends on atomic number. This measure represents large energy scale physics, and the relationship shown in Figure 3(C) is authoritative and robust, not easily broken.
The chemical composition of these compounds is BiTeX (X = Cl, Br, I), exhibiting a layered crystal structure. Among them, BiTeCl has the P63mc space group, while BiTeBr and BiTeI have the P3m1 space group. It is easy to determine from the crystal structure that these compounds are non-centrosymmetric polar semiconductors. Previous experimental measurements have determined the linear splitting factor defined by Figure 3(A), finding that the obtained values are two orders of magnitude larger than those of ordinary narrow bandgap semiconductors, indicating a huge SOC effect! If so, this class of compounds could serve as excellent materials for topological quantum and spintronic applications.
Indeed, Bi is an element with a large intrinsic SOC, but the experimental inference of such a significant Rashba effect for this layered structure still leaves one feeling uneasy. Such doubts certainly linger in the minds of many experienced quantum materials researchers. The young scholar Dr. Jonathan Sobota from Stanford University and the Stanford Institute for Materials and Energy Sciences, who seems to be a student of the renowned physicist Shen Zhixun or a member of Shen’s large team, together with Shen and others, formed a large experimental-theoretical collaborative team dedicated to cutting-edge explorations in quantum materials, yielding fruitful results. Recently, they systematically investigated the spin-related electronic structure of the compound BiTeCl using spin-resolved angular-resolved photoemission spectroscopy (spin-resolved ARPES). The results seem to indicate that beyond the previously understood enormous Rashba effect, there exists a richer physics. The experimental findings suggest that simply attributing the observations to an “unusual” SOC effect may be an oversimplification.
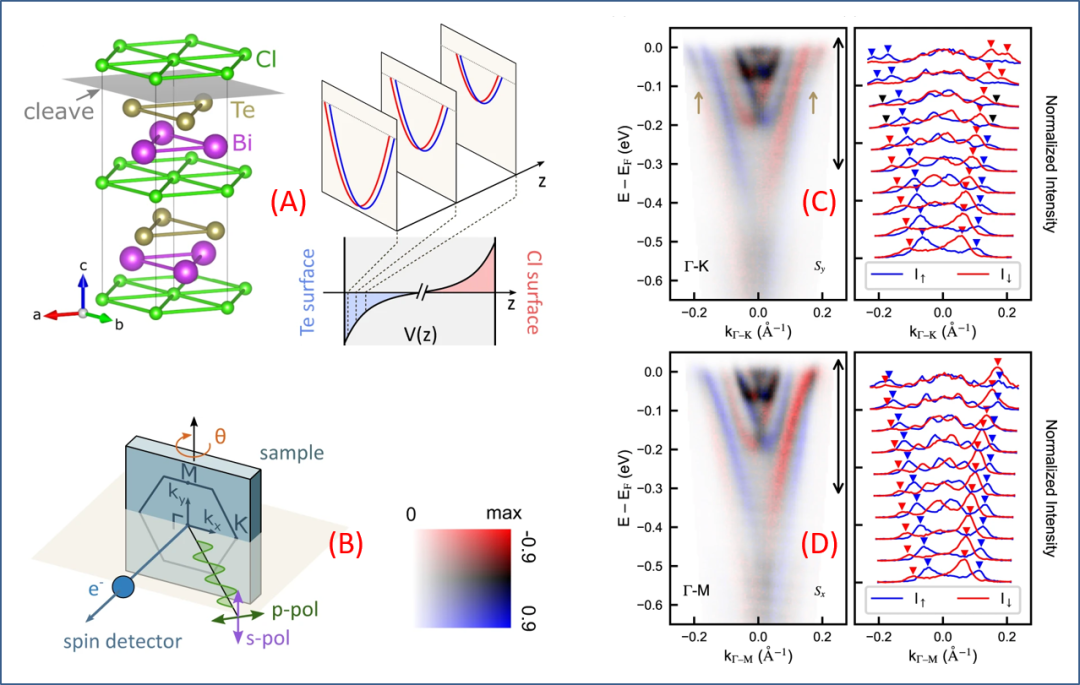
Figure 4. Some results obtained by Dr. Sobota and his team. (A) The crystal structure of BiTeCl and the band structure of Te-terminated samples. Each trilayer forms a structural unit, with a π/3 in-plane rotation between trilayers. The band structure changes significantly as one moves from the Te-terminated crystal surface into the bulk. At the same time, each band exhibits Rashba spin-splitting effects, splitting into two sub-bands. (B) A schematic diagram of the spin-resolved ARPES measurement device and method, including rotating samples for momentum tuning. (C) The Sy-resolved band structure measured along the Γ–K direction, where the spin polarization reversal phenomenon near the Fermi surface is clearly visible (indicated by the orange arrows). The corresponding spin-dependent momentum distribution data is shown in the right-side figure. (D) The Sy-resolved band structure measured along the Γ–M direction, where the band inversion near the Fermi surface disappears.
Once again,Ising demonstrates the skill of “gobbling up information haphazardly”, which is a form of “temporary reliance on superficial knowledge”. I will write down a few notes after studying the work of Dr. Sobota and his team to present my superficial impressions:
(1) Based on the specific P63mc structure of BiTeCl, the spin-resolved ARPES technique can extract electronic structure details of both surface states and bulk states separately, unlike previous analyses that treated this system as homogeneous. This improvement vividly highlights the differences between the surface and bulk states of this system.
(2) The analysis results clearly demonstrate that each trilayer in the system constitutes a primitive unit, as shown in Figure 4(A), with electronic states being relatively localized, and there is a significant difference between surface states and internal bulk states. Additionally, in the out-of-plane direction, the entire crystal structure shows an in-plane rotation of π/3 between trilayers. Although each trilayer exhibits 3m symmetry, the overall structure presents 6mm symmetry. This structural feature is the root cause of the significant differences between surface and bulk states.
(3) The spin-resolved energy spectrum clearly shows that the out-of-plane spin polarization of adjacent trilayer units is reversed, i.e., the reversal of out-of-plane spin texture, which is a result that previous studies did not observe. The band inversion caused by spin polarization reversal occurs near the Fermi surface. Therefore, when understanding the SOC effect and constructing the Rashba Hamiltonian, it is essential to consider the cubic Rashba term, as shown in Figure 3(B). Only then can one comprehensively explain the electronic structure of this system and the strength of the SOC/Rashba spin-splitting factor.
Some results obtained by Dr. Sobota and Shen Zhixun and their team are integrated in Figure 4; readers can refer to the figure title and detailed descriptions in the paper. Interestingly, this work seems to have the flavor of “losing something in the east and gaining something in the mulberry”, as it prompts us to rethink the enormous Rashba spin-splitting effect previously recognized, suggesting that “unusual phenomena often have weird causes”, although here “weird” is more of a positive term. On one hand, it supports the recognition of the authority of energy scales in condensed matter physics; on the other hand, it reveals that higher-order SOC effects may hold value for future applications in topological quantum and spintronics.
However, the defect in this result and recognition lies in that similar large spin-splitting effects have also been observed in BiTeBr and BiTeI, which are homologous to BiTeCl. Due to the differences in lattice symmetry, the analysis for BiTeCl may not be directly applicable to BiTeBr and BiTeI. This defect also somewhat limits the universality and promotion significance of Dr. Sobota’s work. It is evident that physicists still need more exploration to see how to improve this work.
One last point worth pondering is that this work subtly questions and supplements past significant discoveries. The authors express this questioning in a gentlemanly manner, implying concerns and doubts about their peers’ results while striving to present data, analysis, and expression as scientifically and objectively as possible, without any emotional cadence. This attitude and demeanor of addressing matters objectively, being restrained, and leaving conclusions for readers to judge is commendable.
The unchanging conclusion:Ising is an outsider; please forgive any omissions in the description. For those interested, please refer to the original text. The link to the original article is as follows:
Reversal of spin-polarization near the Fermi level of the Rashba semiconductor BiTeCl
J. Qu, X. Han, S. Sakamoto, C. J. Jia, J. Liu, H. Li, D. Guan, Y.-J. Zeng, M. Schüler, P. S. Kirchmann, B. Moritz, Z. Hussain, T. P. Devereaux, Z.-X. Shen & J. A. Sobota
npj Quantum Materials 8, Article number: 13 (2023)
https://www.nature.com/articles/s41535-023-00546-x
Five-Character Regulated Verse·Qiantang River Confluence
Rippling white waves, caressing the face with their dance
Wishing to kiss the swaying life, distant thoughts hidden in torrents
Crossing lines, holding on to the long river
Do not waste this moment, encounters may not come often

Note:
(1) The author Ising, works at the School of Physics, Nanjing University, and is a part-time editor of npj Quantum Materials.
(2) The title of this article “Unusual Phenomena in SOC” is an emotive expression, not a rigorously physical statement. It merely conveys that in quantum materials, the authority of energy scales still applies. If there are unusual results, seeking new physics rather than amplifying the “unusual” itself may be a more reliable thought and path. Of course, this article does not say “there must be weirdness” but uses “there are often weird causes” to express that things should not be absolute. Here, “weird” is more positive than negative.
(3) The images at the bottom are sourced from the internet, showcasing the tidal confluence of the Qiantang River (https://www.toutiao.com/video/7126021650306302478/). This five-character verse (20230912) originally describes the beautiful forms of the tidal confluence of the Qiantang River, used here to illustrate the quantum materials band structure revealed by spin-resolved ARPES. It can be seen that both the tidal flow and ARPES band structure are similar and unified in form and intrinsic beauty.
(4) The cover image displays the spin-resolved band structure obtained by Dr. Sobota and his team, clearly illustrating the spin polarization reversal effect.
Selected Articles
A New Path to Large Berry Curvature
Room Temperature Electromagnons— The Redemption of Multiferroics
Liquids Are Always So Picky, Fermi Liquids Too
Following “Yao-Li” to Characterize Quantum Spin Liquids
Mastering Topological Quantum Transport in Quantum Oscillations
Elusive: Charge Stripe Phase in Copper-Based Superconductors
It’s Okay Not to Have Long-Range Order:RIXS Probing Berry Curvature andOAM
Spin Triplet Pairing Density Waves— A Brand New Exotic Quantum State
Does Quantum Magnetism Have a Spectrum?— YesSU(3) Neutron Scattering Spectrum
Though Not Easy, It Can Be Easily ReachedLifshitz Phase Transition
Welcome to Subscribe to npj Quantum Materials Email Alerts
Click https://idp.nature.com/register/natureuser to complete the free subscription
