SIMD has played an increasingly important role in processors in recent years, providing significant performance improvements for multimedia applications, and most computations within GPGPU warps are also performed in a SIMD-like manner. Understanding SIMD is crucial for a comprehensive understanding of architecture. This book provides a comprehensive and detailed introduction to the design concepts and microarchitecture implementation methods of SIMD. It first compares SIMD with other parallel technologies, including superscalar, multithreading, and multicore technologies, and then introduces the three most important aspects of SIMD: 1. Computation and control flow; 2. Memory operations; 3. Horizontal operations. It is one of the few good books on SIMD.

This is a reading note for the book “Single-Instruction Multiple-Data Execution” from the Synthesis Lectures on Computer Architecture series, published in 2015, with some personal insights added for record-keeping and collaborative learning.

1. Data Parallelism

1.1 Data Parallelism

The simplest definition of data parallelism is: “performing the same operation X on data a to z,” and such operations are very common in real applications, especially in applications that process/model real-world physics, such as multimedia/sensor data processing, 3D modeling, etc.

However, different operations on different data can also exhibit data parallelism (for example, branch instructions performing different operations on different categories of data), so a more general definition is: “For a set of independent data, a single code segment can represent them, and they all have the same starting point” (similar to SIMT).

1.2 Data Parallelism in Applications

1.2.1 Physical Simulation

Used to simulate different types of physical phenomena, such as fluids, fabrics, hair, muscles, etc. CFD (Computational Fluid Dynamics) is used to simulate fluid motion, typically solving the <span>Navier-Stokes</span> equations under certain precision, which describe the velocity field of fluids at a given time. A common solution is to discretize the space being simulated into a three-dimensional grid and then use finite difference methods to compute each voxel, essentially updating the voxel at regular time intervals, as shown in the figure below. Essentially, each point can be updated in parallel, and the computation function is the same.

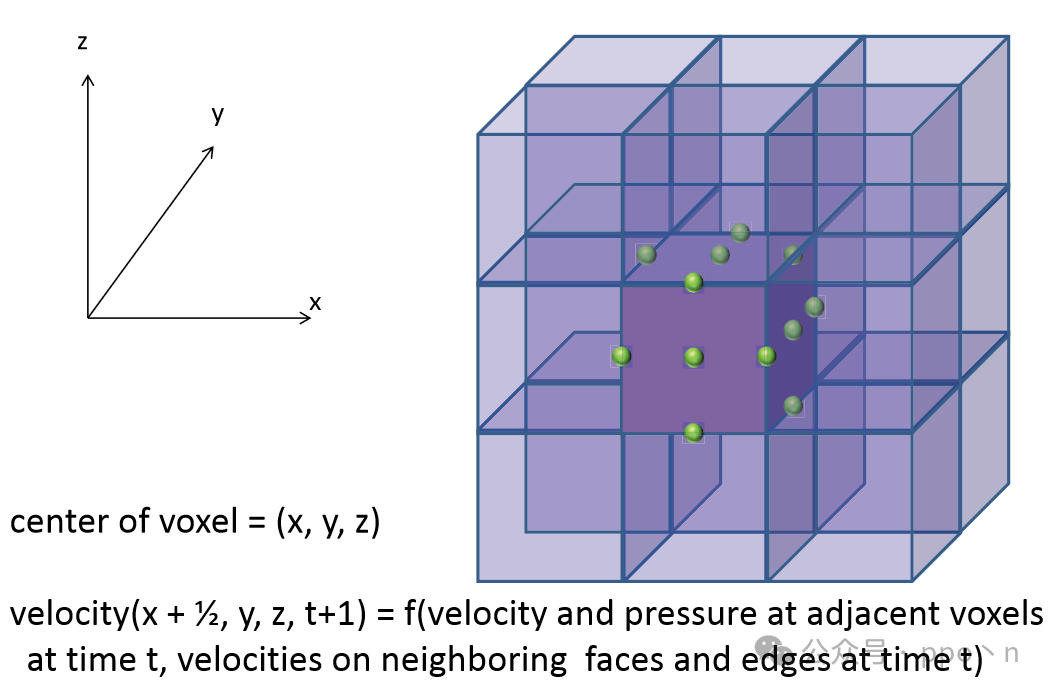
1.2.2 Computer Vision

Such as face detection, automatic hypothesis, etc., processing image data transmitted by cameras, using a mix of traditional image processing and machine learning. A simple example is median filtering, where for an nn image, n such operations need to be performed, which is also data parallelism.

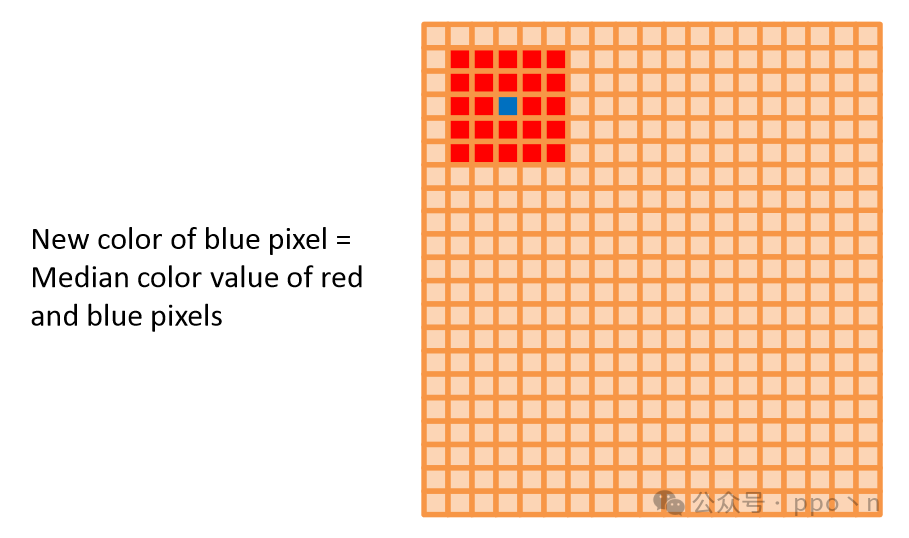
1.2.3 Speech Recognition

The main steps include: a. Extracting features from raw audio; b. Judging possible semantics based on current and previous segment features. A common algorithm in feature extraction is WFST (Weighted Finite State Transducer), which is a state machine that includes acoustic models, pronunciation models, and language models, as shown in the figure below (similar to a neural network but not fully connected), so state calculations can also be performed in parallel.

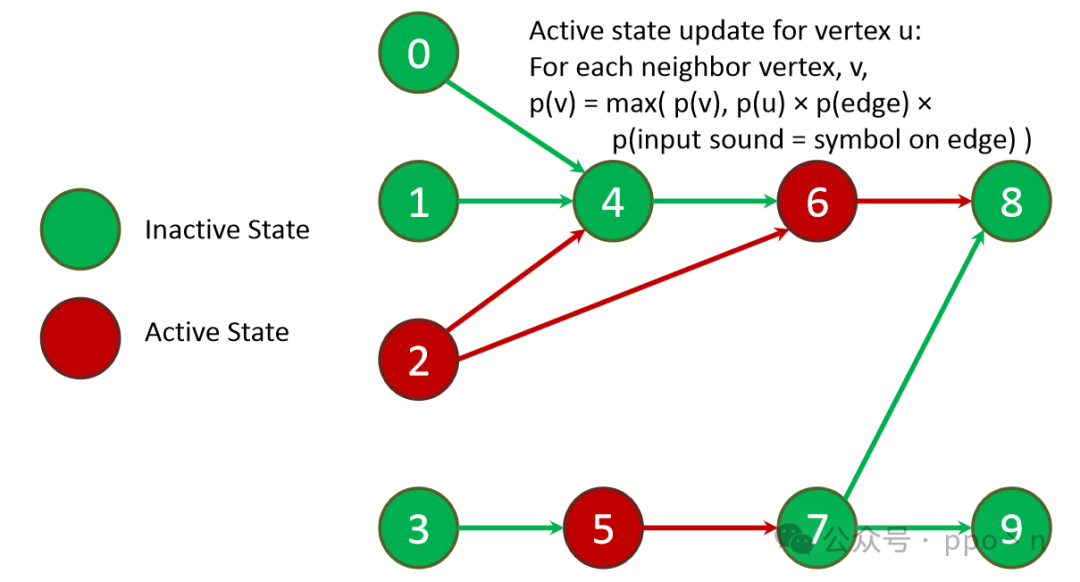
1.2.4 Database Management Systems

Used for processing queries that combine data, exhibiting data parallelism for queries that do not want to exchange data within the database.

1.2.5 Financial Analysis

Such as derivative pricing, determining whether to buy or sell at a given price, with computational equations also exhibiting data parallel characteristics.

1.2.6 Medical Imaging

Such as MRI or X-ray scans, typically requiring 3D modeling, with computations at different points in time exhibiting data parallelism.

2. Utilizing SIMD for Data Parallelism

2.1 Utilizing Data Parallelism

Options to increase the performance of a single processor core include:

• Increasing the frequency of the processor and memory system, or optimizing the microarchitecture to reduce instruction execution or memory access latency
• Typically used to accelerate serial execution instructions rather than parallel execution
• Executing more instructions simultaneously, which can be achieved through wider superscalar architectures or increasing the number of threads
• This utilizes instruction-level parallelism (ILP), which also includes data parallelism, making it more general rather than only targeting data parallelism
• Increasing the workload of each instruction execution
• Many such types of instructions exist in CISC

SIMD is a combination of the last two methods above, where a single instruction can execute multiple tasks, but it requires that the tasks are independent operations. It specifically targets data parallelism.

2.2 SIMD Execution

Early vector processors specified operations between two long vectors, but the underlying hardware could perform multiple operations in each cycle, with vectors stored in dedicated vector registers, allowing the same program to run on different hardware (such as newer RISC-V RVV). Early vector processors typically used deeply pipelined execution units to achieve higher frequencies, requiring long vectors to cover the pipeline depth, which could be satisfied for some server-side applications.

However, today, for some consumer applications, shorter vectors are more common, so today’s processors utilize SIMD to handle them, typically having a fixed number of 2-8 elements, and no longer using deep pipelines but rather multiple parallel processing units to complete operations within a single cycle.

2.3 Performance and Energy Efficiency Gains of SIMD

SIMD has two properties that translate into advantages in different aspects of microarchitecture:

1. Combining multiple operations into a single compact instruction
2. Explicitly indicating that the operations contained are independent

This section will specifically compare SIMD technology with some other more general technologies that can utilize data parallelism, including:

1. Superscalar processors, which can issue multiple instructions per cycle
2. Multithreaded cores, which can execute computational instructions from multiple threads
3. Multicore processors containing multiple scalar cores

The table below lists the hardware behaviors of these technologies utilizing data parallelism in different parts of the microarchitecture.

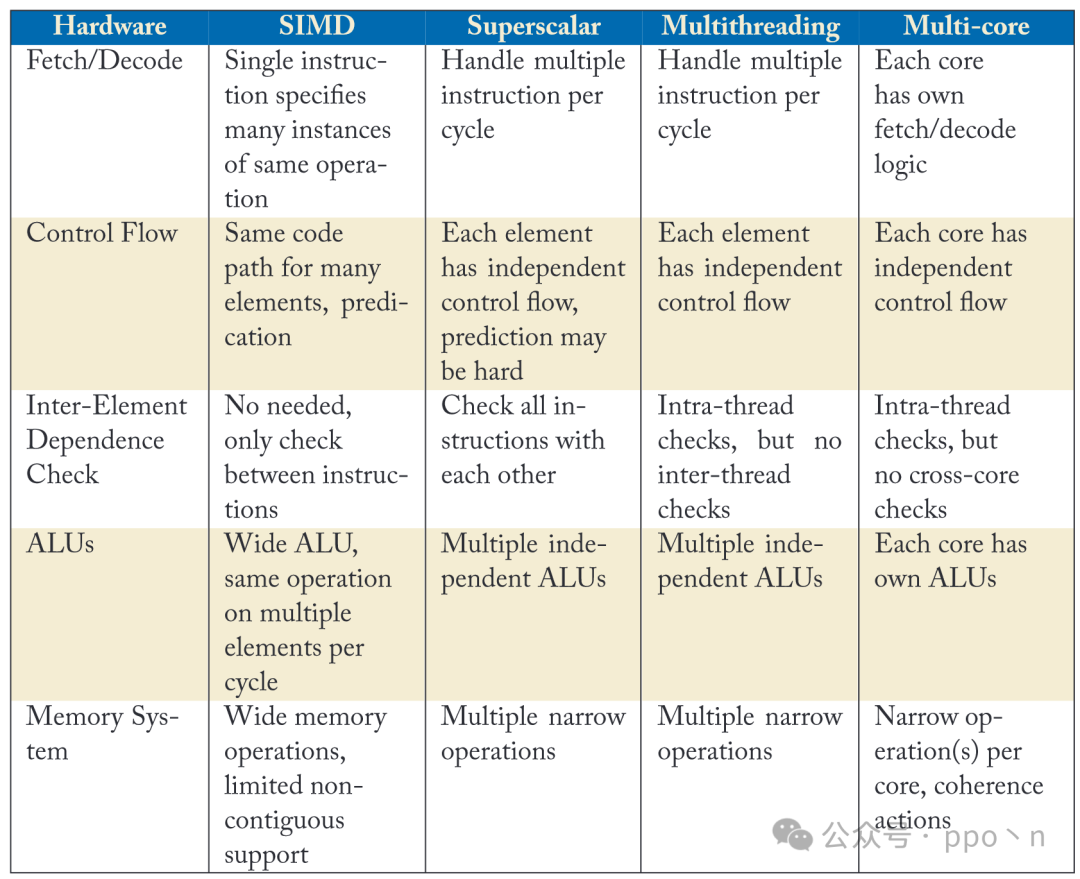
The image below also provides a more detailed illustration of its hardware behavior.

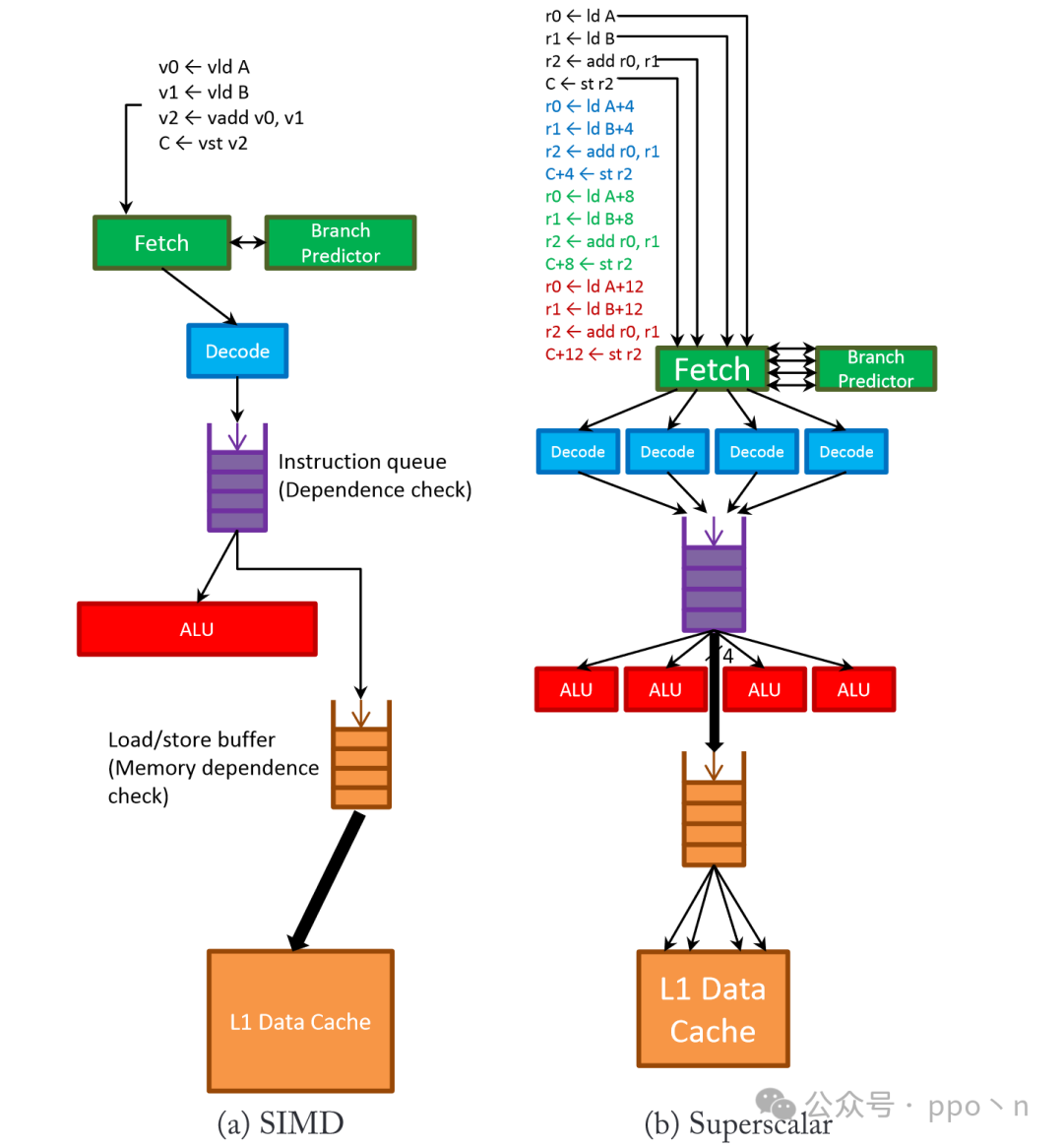
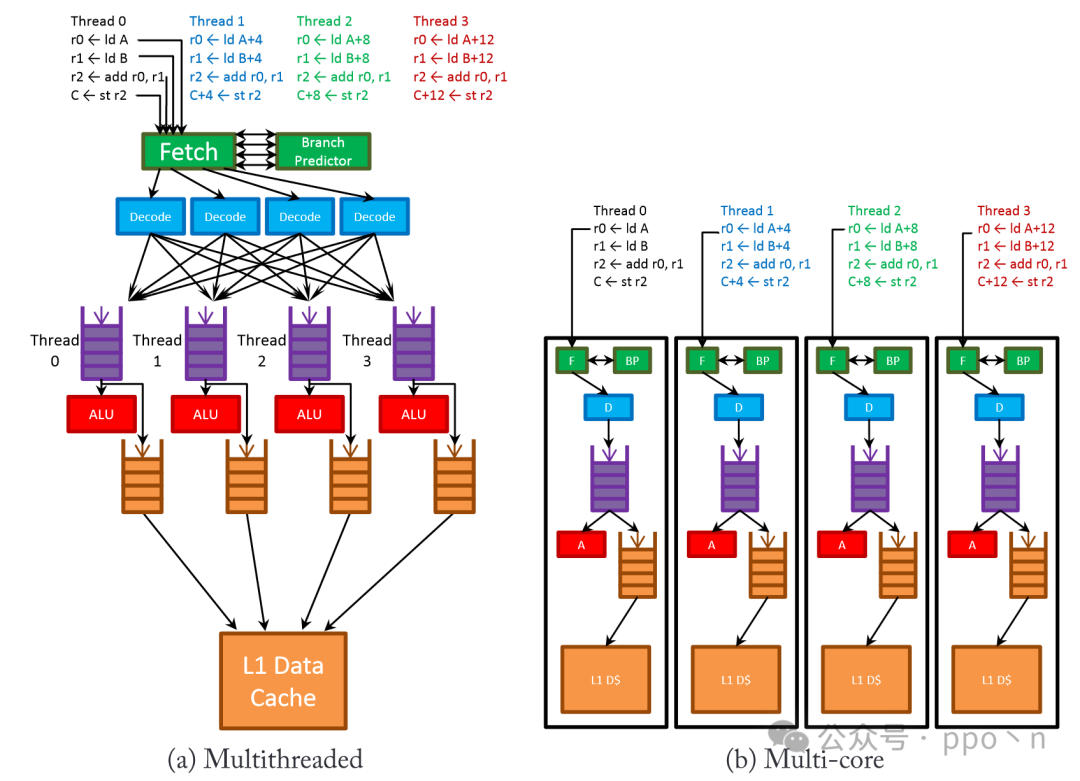
In comparison:

• Fetching and decoding parts
• SIMD design only needs to process one instruction at a time to carry multiple effective operations to the execution unit, saving related control and decoding logic
• The trade-off for SIMD is that it is only efficient for data parallelism, while other instructions can only run inefficiently, but other designs can still accelerate to some extent, such as parallelism between threads
• Execution part
• SIMD requires multiple parallel ALUs, but the cost is lower than other solutions because there is no need to duplicate control logic
• SIMD does not need to check dependencies between data within a single instruction, only inter-instruction dependencies need to be checked, similar to how simple scalar processors compare source and destination registers
• Multithreaded and multicore processors, similar to SIMD, only need to check dependencies within a single thread or a single core
• The overhead for superscalar processors is greater, as dependencies between multiple parallel instructions need to be checked each cycle
• SIMD does not require complex control logic, although some designs use predication to run control instructions, but the cost is still much lower than other designs
• Other designs have completely independent control flow paths
• Control paths
• Dependency checks
• ALU
• Memory part
• SIMD usually needs to support wider memory accesses and may also support non-contiguous data accesses, which may require additional hardware to check memory access dependencies or increase buffers to speed up access, especially for non-contiguous address accesses
• Similarly, to achieve the same bandwidth, superscalar and multithreaded designs also need to support issuing multiple independent read/write instructions per cycle, which is similar to SIMD’s access to non-contiguous addresses, and may even be more costly because they also need to check dependencies between read/write instructions accessing in parallel.
• Multicore designs are relatively simple, as each core can replicate the memory access path, but coherence and consistency are significant issues

Overall:

• SIMD is optimal in terms of area, power consumption, and complexity for utilizing data parallelism, but sacrifices generality.
• Multithreaded and multicore designs have higher costs because each thread needs to replicate some hardware, but can utilize thread parallelism, even if they run completely unrelated operations
• Superscalar costs are higher, as hardware needs to be replicated at every stage of the microarchitecture, and complexity grows superlinearly, with the payoff being its generality, allowing it to extract instruction-level parallelism from a single thread.

In real scenarios, designs typically use a combination of the above technologies. Server-side processors like Intel Xeon utilize a mix of these technologies. Superscalar is a design approach favored by programmers because they tend to design serial algorithms, but superscalar processors can only achieve limited instruction throughput; SIMD can efficiently utilize data parallelism and integrate it into superscalar cores without significantly increasing costs to achieve higher throughput; multithreading can help improve the utilization of superscalar cores, hiding long-latency operations, but too many threads can put significant pressure on the memory system; finally, multicore designs provide a very scalable way to increase the overall throughput of the processor, with the cost of replicating cores and software parallelism making it a last resort, used only when the performance and cost are deemed optimal.

2.4 Limitations of SIMD Scaling

The overhead of instruction fetching and decoding is independent of SIMD width; execution units grow linearly with SIMD width; the memory system becomes more complex as SIMD increases:

• For DCache
• Increasing cache line length, but the downside is that performance for non-contiguous memory accesses will decrease, and bandwidth utilization will drop
• Increasing cache port numbers, however, area, power consumption, and latency grow superlinearly with the number of ports, even using banking techniques can only be used for non-contiguous accesses, and there are physical limitations in scaling
• As SIMD width increases, a single memory operation may hit multiple cache lines, which can be improved in two ways
• For TLB
• Increasing page size may lead to reduced memory utilization
• Increasing TLB throughput may lead to superlinear growth in overhead
• If SIMD width is very large, it may hit multiple pages, leading to the same dilemma as DCache

The above are physical design limitations, and actual designs are also constrained by algorithm limitations, as real algorithms often include a large number of scalar steps.

Define<span>SIMD Efficiency</span> as the ratio of instruction count reduction of SIMD version code to vector length, as shown in the following formula. For example, if the SIMD version program is 1/4 of the scalar program, then the instruction reduction is 4, and if the vector length is 4, then SIMD Efficiency is 100%.

If the SIMD program and scalar program have the same latency and throughput, then the instruction reduction is the speedup seen in SIMD. If SIMD instructions execute slower (which is usually the case), then the SIMD speedup will be less than the instruction reduction.

The following figure shows the SIMD Efficiency under different vector widths and different proportions of scalar instructions. Here it is assumed that the scalar to vector conversion does not introduce additional instructions and that SIMD instructions run as fast as scalar instructions. This figure reflects the application of Amdahl’s Law to the speedup of SIMD execution.

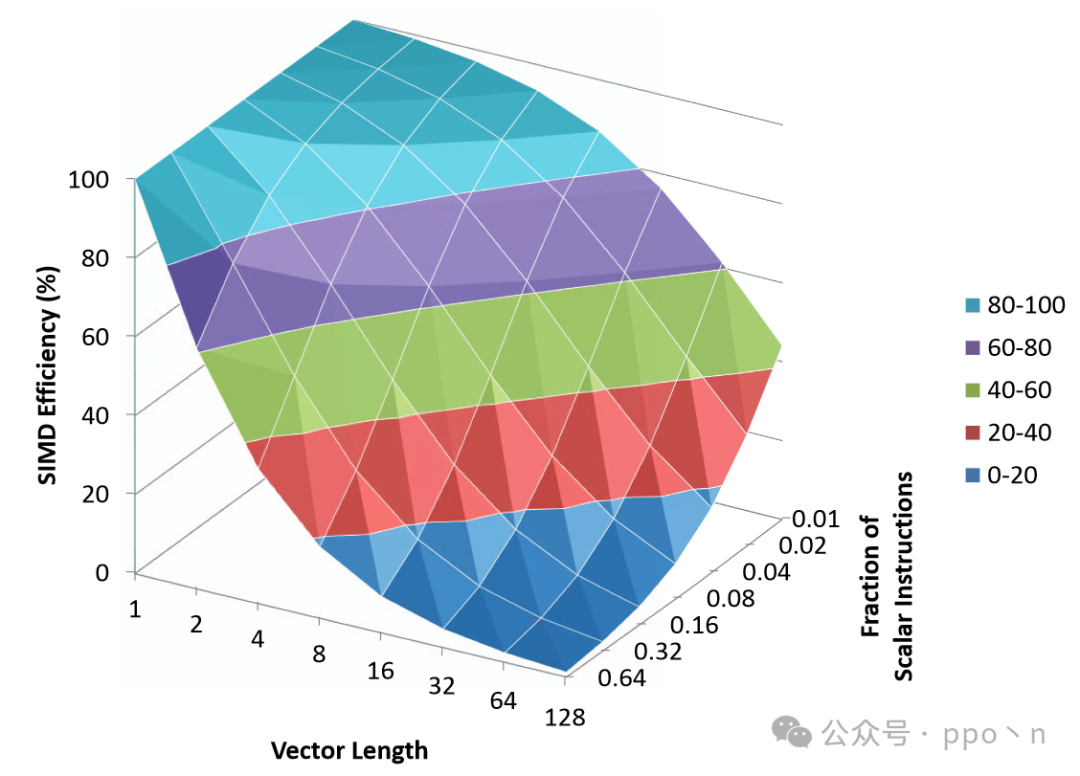
This assumption does not conform to reality but can provide a reference for the upper limit of SIMD execution speedup. The longer the vector length, the smaller the proportion of scalar instructions will lead to a rapid decline in SIMD Efficiency.

Another inefficiency in SIMD execution arises when data items are not multiples of the vector length, leading to remainders that cause some invalid executions (which can be completed by scalar execution or masked out using Predicated). The code that does not handle remainders is as follows:

for (i = 0; i < N; i += VLEN) 
{
  vload v1, A[i] 
  vadd v0, v1, v2 
  vstore B[i], v0 
}

The following figure shows the impact of loop remainders on SIMD Efficiency. The upper figure uses scalar instructions for the remainder, while the lower figure uses Predicate to handle the remainder.

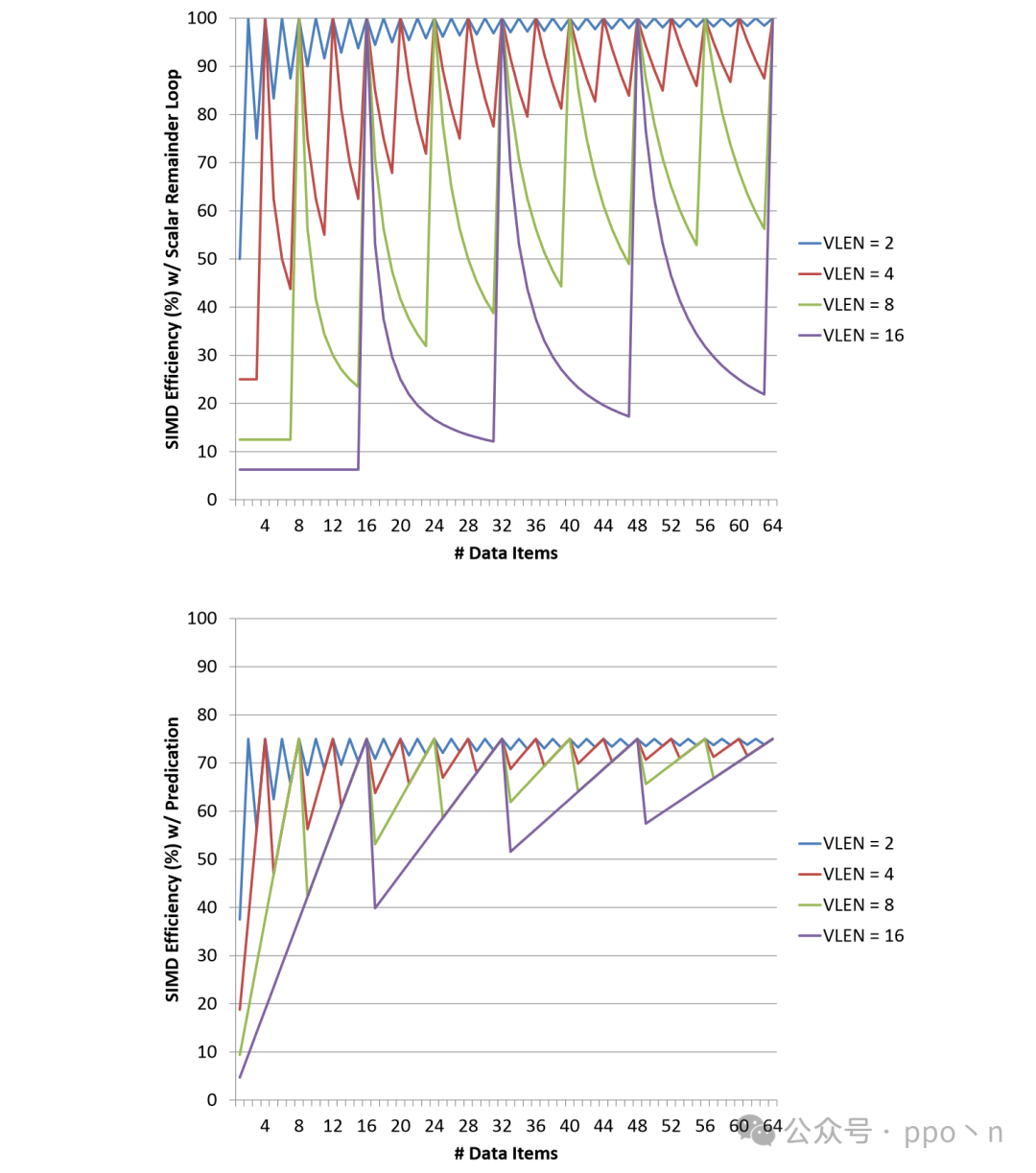
As the amount of data increases, the impact of the remainder diminishes; as VLEN increases, the impact of the remainder increases. The main overhead of the Predicate method is the computation of the Predicate register, and its overall effect is better than the scalar method. How to increase the flexibility of SIMD design to improve SIMD Efficiency is an important issue, with proposed solutions including dataflow design or software-assisted methods.

2.5 Programming and Compilation

SIMD instructions need to be manually inserted by programmers or automatically generated by compilers, which is a relatively large topic, but this article mainly focuses on architecture and does not detail these topics.

2.5.1 Programming SIMD Execution

Programmers can execute SIMD through assembly or inline assembly, which is relatively higher in performance (even as of 2025, automatic vectorization compilation tools are still not very mature, and some high-performance scenarios, such as the underlying SIMD execution of the OpenCV library, are still manually written by programmers).

2.5.2 Challenges of Static Analysis

These are some challenges faced by compilers in automatic vectorization, many of which are SIMD architecture issues. Due to hardware costs and other reasons, it is impossible to perform complete dynamic dependency and control flow checks, leading compilers to conservatively complete only a portion of the program’s vectorization.

• Determining where/what to vectorize
• Determining if all data items have the same control flow
• Determining if data is aligned
• Understanding how data is organized
• Determining the safety of vectorizing the memory operations

3. Computation and Control Flow

This chapter describes non-memory components related to SIMD, including data storage (registers), computation instructions, and control flow.

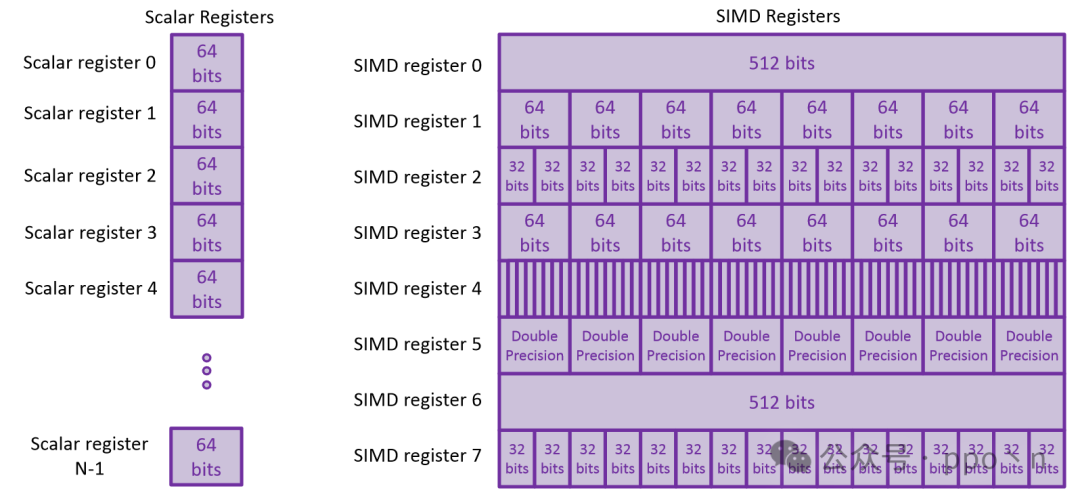
3.1 SIMD Registers

SIMD data can be stored in dedicated SIMD registers (Intel’s SSE and AVX) or across multiple general-purpose registers (Sun’s VIS). (Most modern processors use the first method).

The figure below shows scalar registers and vector registers, where scalar registers are physical registers, so for designs like superscalar processors with renameable units, they will have more than architectural registers. SIMD registers are relatively wide, and due to their size, they usually limit their quantity, so register renaming techniques are rarely used.

3.2 SIMD Computation

3.2.1 Basic Arithmetic and Logic

Computation types mainly include

• Arithmetic operations (addition, subtraction, multiplication, and division)
• Boolean operations (and, or, xor)
• Logical and arithmetic shifts
• Data type conversions
• Data selection operations (min, max)

Example code is shown in the figure below.

3.2.2 Data Element Size and Overflow

For SIMD, the smaller the data element width, the more operations it can execute simultaneously, so using compact data types can achieve higher performance. However, reducing data width can lead to more frequent overflows, and common methods include using carry bits for addition or placing results in larger registers for multiplication.

For SIMD, a more common approach is to provide<span>saturating arithmetic</span> instructions, which represent values exceeding the range using the maximum or minimum value that can be represented.

3.2.3 Advanced Arithmetic

Mainly includes:

• Transcendental functions and other nonlinear functions, including sin, cos, etc.
• <span>horizontally</span> operations, used to operate on elements within the same SIMD register
• For example,<span>horizontal add</span> computes the sum of all elements within a SIMD register
• <span>Shuffle</span> instructions are used to swap positions of elements within SIMD

3.3 Control Flow

The control flow in SIMD programs is similar to that in pure scalar programs, including loops, function calls, etc. However, when different elements in SIMD execute different code paths, some issues arise, known as<span>control divergence</span>.

3.3.1 SIMD Execution with Control Flow

<span>control divergence</span> issues may arise from if-checks, inner loops, or switches. The following example contains if-check vector loop code, where a hardware-independent method is to first speculatively execute all vector computations, write to a temporary buffer, and then use scalar execution to submit the execution results.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
if (A[i] > 0) 
  { 
    B[i] += C[i]; 
  } 
}
// Simple vectorized version 
for (i = 0; i < N; i += VLEN) 
{ 
vload v0, B[i] 
vload v1, C[i] 
vadd v2, v0, v1 
vstore buffer, v0 

for(j = 0; j < VLEN; j++) 
  { 
if (A[i + j] > 0) 
    { 
      B[i + j] = buffer[j]; 
    } 
  } 
}

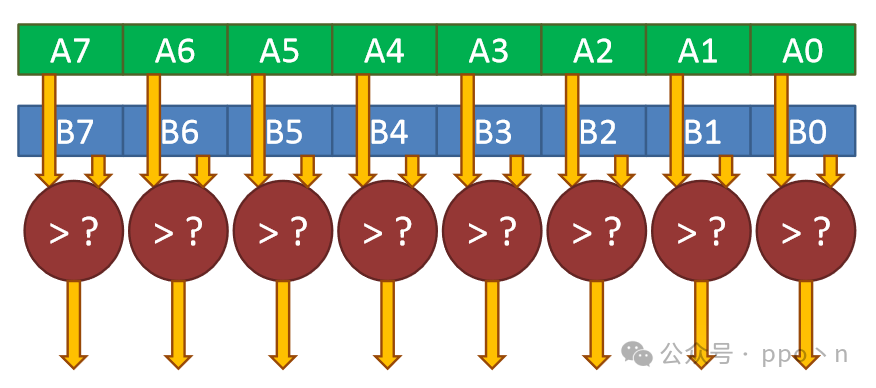
A drawback of the above code is that it may access data that the original scalar program would not access; for example, if A[i]=0, it would not access the corresponding B[i] and C[i], but the vector program below would still access them. Additionally, control conditions can also be executed in parallel, as shown in the figure below. Each of these computation results only requires 1-bit data to be stored, so dedicated registers are usually used to store these results, some of which are called<span>predicate registers</span>.

3.3.2 Conditional SIMD Execution

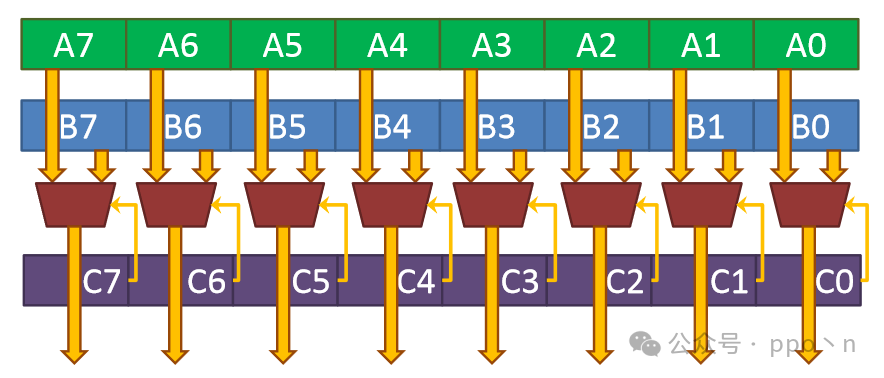
The software solution using scalar instructions to address<span>control divergence</span> is very inefficient. Another approach is to utilize<span>Blend instruction</span>, which takes input data A and B and control input C for conditional execution and computation, as shown in the figure below.

Many modern architectures provide an implicit blending instruction through the use of<span>masking</span>, which uses predicate registers, where each bit indicates whether the instruction should apply to the corresponding data. This method has many benefits:

• More registers are available for SIMD Data
• Less storage space is wasted
• No need to add extra read ports on SIMD registers

The following shows an example of conditional SIMD execution, where registers starting with m are mask registers.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
if (A[i] > 0) 
  { 
    B[i] += A[i] + C[i]; 
  } 
} 

// Vectorized version with masking 
for (i = 0; i < N; i += VLEN) 
{ 
vload v0, A[i] 
vxor v1, v1, v1 
vcmpgt m0, v0, v1 

  vload v2, m0, C[i] 
vadd v3, m0, v0, v2 

  vload v4, m0, B[i] 
vadd v5, m0, v3, v4 
vstore B[i], m0, v7 
}

Additionally, the mask does not necessarily have to be explicit. Some modern GPUs use<span>implicit masking</span>, where the mask register is not an architectural register but is automatically computed and masked by hardware.

For memory accesses, masking cannot be simply applied because there are some address ranges with side effects, such as device memory, which may read/write clear, so hardware needs to ensure that these risky accesses do not occur, either by accurately masking before executing memory accesses or providing a<span>fault suppression</span> mechanism to avoid side effects.

3.3.3 Impact of Control Divergence on Efficiency

Control divergence can waste vector elements in SIMD instructions, thus affecting efficiency. The figure below shows the effective data ratio under different levels of nesting for each divergence with infinite SIMD width.

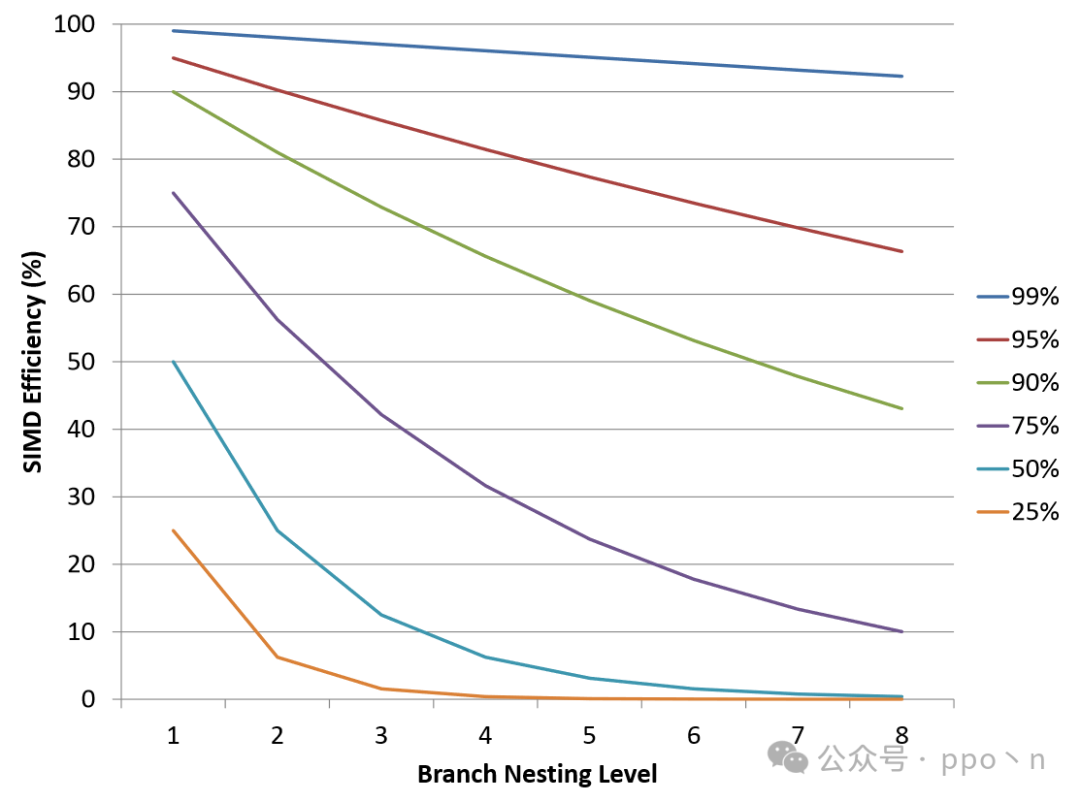
It can be seen that the effective data ratio under a single SIMD execution divergence has a significant impact on SIMD efficiency at different levels of nesting, but typically the efficiency under normal conditions does not drop too low, as at least one element among multiple elements will execute, meaning the efficiency is at least, especially when many processors have low SIMD widths, such as 4, leading to at least 25% efficiency. Therefore, many low-width SIMD designs do not focus on control divergence, such as Intel only introducing masking in AVX-512.

4. Memory Operations

4.1 Continuous Patterns

This is the most common memory access pattern in data parallel computing, which is also intuitive and easy to implement. Compared to scalar, it only needs to support a larger memory data width. In traditional scalar caches, to utilize spatial locality, cache lines will also contain multiple data, so hardware changes are almost unnecessary until a certain extent is reached.

If SIMD width exceeds cache line width, then

• Either perform memory accesses over multiple clock cycles, executing a SIMD memory operation, which may affect efficiency
• Or increase cache line size

4.1.1 Unaligned Access

Even if SIMD width does not exceed cache line size, unaligned accesses may still lead to accesses to different cache lines, which is called<span>cache line split</span>. The figure below shows three different unaligned access patterns, where the first and third both experience cache line splits.

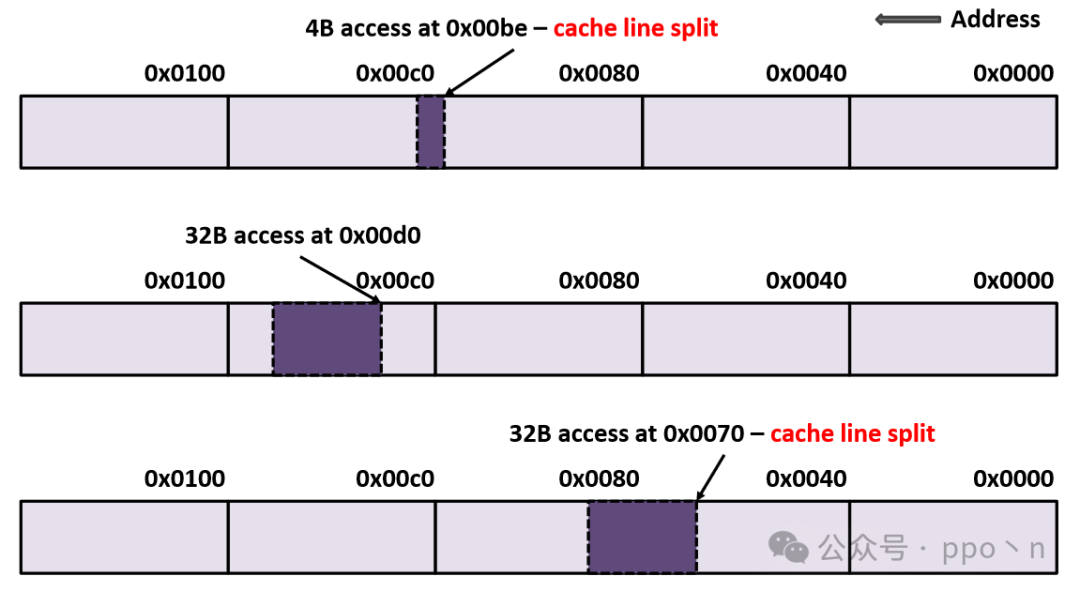
For<span>cache line split</span><span>, the cost of simultaneously accessing two cache lines in parallel is very high, so modern architectures that support unaligned accesses typically implement this through multi-cycle accesses. Although this approach halves memory access performance, it does not significantly impact scalar data access because:</span>

• Most data accesses are aligned, especially for continuous access patterns
• Scalar data is much smaller than cache line size, so the chance of crossing cache lines is low

In contrast, the likelihood of SIMD memory accesses crossing cache lines is much higher, requiring significant software or compiler assistance to mitigate its impact.

4.1.2 Throughput Impact

The frequency of cache misses and crossing cache line accesses during SIMD memory accesses is greatly increased. However, they are not the biggest performance issue compared to unaligned access patterns, because for continuous accesses, simple prefetching can cover most cache misses.

Additionally, streaming or non-temporal stores can be used to improve bandwidth utilization, exhibiting no-write-allocate behavior, meaning data is written directly to memory without needing to read back data before writing, as traditional writes do. This approach has been widely adopted in modern processors, such as the CHI protocol or Nvidia GPGPU.

4.2 Non-continuous Patterns

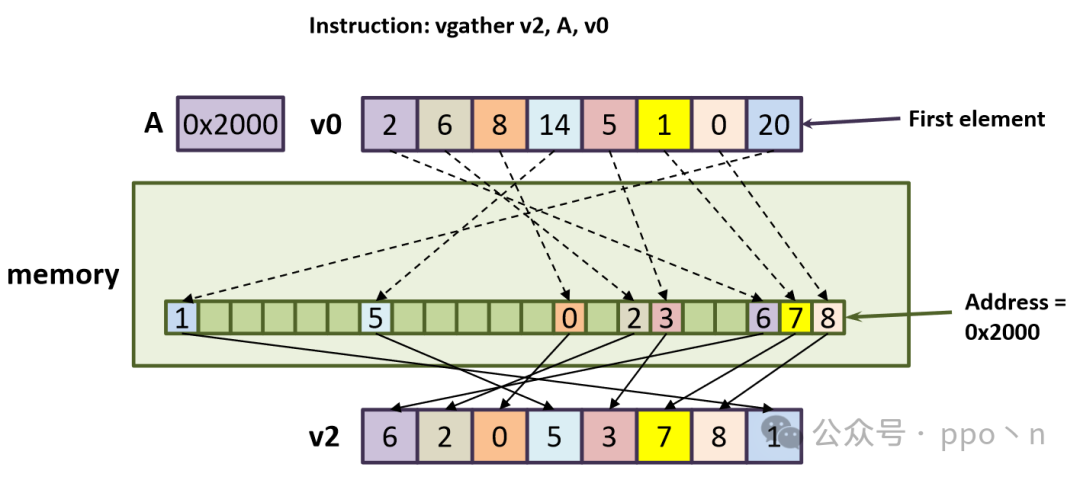
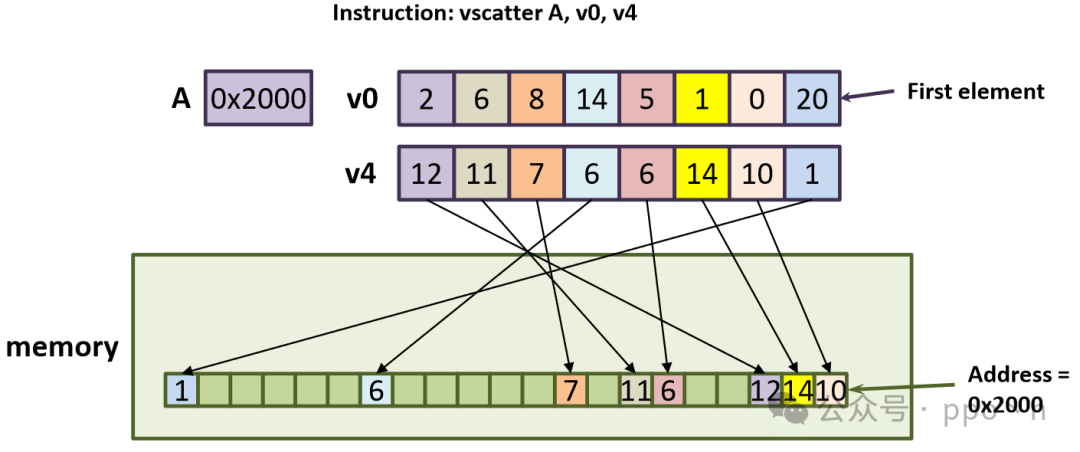
Most non-continuous memory accesses arise from simple array accesses or pointer dereferences, as shown below. Here, B is an integer array containing offsets of A, and ptr is a pointer to an integer array. To vectorize, gather and scatter instructions are used, also known as indexed load/store.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
  A[B[i]] += *(ptr[i]); 
} 

// Vectorized loop with gather and scatter 
for (i = 0; i < N; i += VLEN) 
{ 
vload v0, B[i] 
vload v1, ptr[i] 
vgather v2, A, v0 
vgather v3, 0, v1 
vadd v4, v2, v3 
vscatter A, v0, v4 
}

The figure below corresponds to the first gather instruction, where the memory access intervals will automatically scale according to the data type, for example, A[2] should correspond to address 0x2008.

The figure below corresponds to the scatter instruction in the code.

It is evident that such non-continuous memory accesses can be very inefficient. For unknown access patterns, we can dynamically check if they are continuous patterns. If done in software, the overhead would be very high and not worthwhile. Using hardware would increase area and memory access latency, and some GPUs use this hardware check, while memory-sensitive CPUs use it less.

4.2.1 Programming Model Issues

Completion Mask

Considering virtual addresses, data access needs to first access the TLB to convert to physical addresses for normal memory access, but accessing the TLB may encounter page faults, leading to exceptions that usually require long recovery times, such as being resolved by the OS, and then re-executing the memory access instruction.

For SIMD continuous memory access patterns in load/store, if its width does not exceed the page size, it will access at most 2 pages, leading to<span>page split</span>. If both pages are accessed and encounter page faults, ideally the third access can execute normally, but if the second page table is evicted while fetching the first page table, the situation will worsen, and in extreme cases, if only one page table can be stored, it may lead to the instruction being unable to execute.

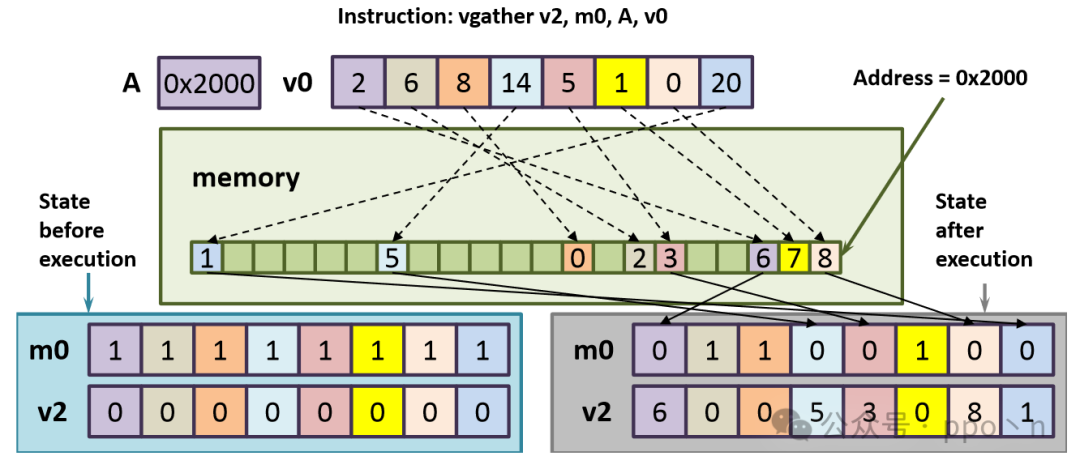
For gather/scatter instructions containing N elements, it may access up to 2N page tables, leading to a much worse situation. A feasible method is to use a<span>Completion Mask</span> register to identify which elements have completed access, allowing these instructions to partially execute, similar to conditional execution in SIMD. The figure below is an example.

Element Ordering

SIMD ordering can be divided into Inter-Instruction and Intra-Instruction, determined by the specific Memory consistency model. For Inter-Instruction, it can be similar to traditional scalar processors, using Load/Store buffers to resolve, but the difference is that it requires gather/scatter instructions to allocate multiple entries at once because it contains multiple data internally.

For Intra-Instruction ordering, the simplest and most intuitive example is when scatter instructions have the same address for writes, as shown in the figure below. The left side shows the scalar execution method, while the right side shows two ordering results for scatter execution, where only the order from front to back conforms to scalar execution.

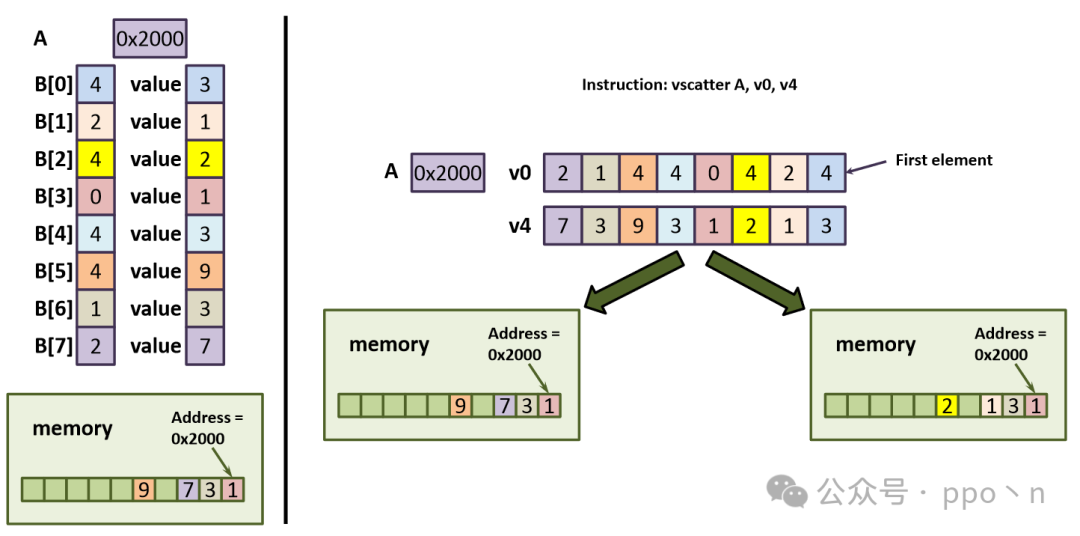
Intra-Instruction ordering can also be simply implemented using Load/Store buffers, meaning that each read/write within scatter is recorded with an entry, making it similar to the Inter-Instruction ordering solution.

Completion Guarantee of Elements

<span>Completion Guarantee</span> describes the state attributes that must be preserved in the target register/memory when the instruction completes (such as passing exceptions). The goal is to ensure that progress can be made. In implementation, care must be taken to avoid getting stuck in an infinite loop, leading to livelock, and to ensure that no information is lost.

4.2.2 Implementation of Gather and Scatter Instructions

First, consider what these instructions do:

1. Split the vector indices and mask bits into individual elements
2. For scatter, also need to split the data into individual elements
3. For each element, scale the index, add it to the base address, and use the mask bit to control the read/write
4. For gather, wait for each element to return before writing to the destination register
5. Clear the completion mask

Hardware within the Core

We only consider the hardware form, and the address calculation method is shown in the figure below, where shifting is used to implement scaling.

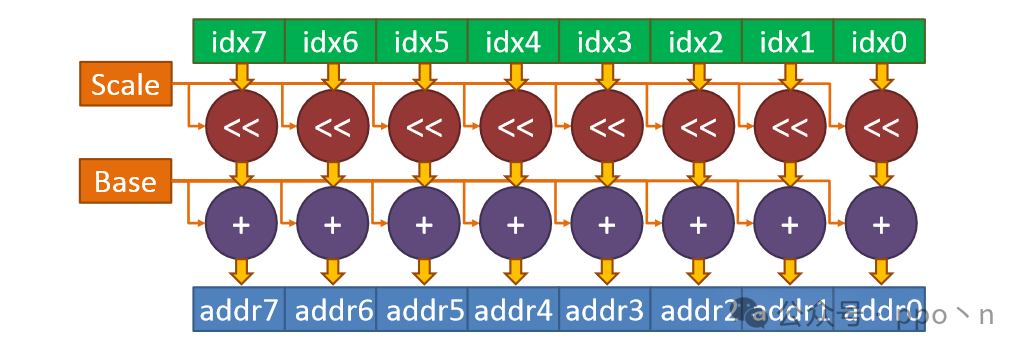
In practice, it may be limited by the access bandwidth of Cache or TLB, and may not complete the above calculations in one cycle, but this depends on the specific design or whether there are dedicated buffers or computing units.

For gather, the next key consideration is merging the returned data into the destination register, which may require an intermediate buffer to cache partial results until all data returns. For scatter, the next key consideration is extracting data, i.e., correctly retrieving data from the source register to the corresponding position.

Combining Elements

Gather or scatter instructions can also exhibit spatial locality, and hardware can use this to improve performance. For example, accessing an entire cache line may satisfy the data needs of multiple positions in the instruction. Some architects refer to this as<span>memory coalescing</span>.

An example is shown in the figure below, where a SIMD memory instruction with 8 elements can be completed in 5 memory access cycles.

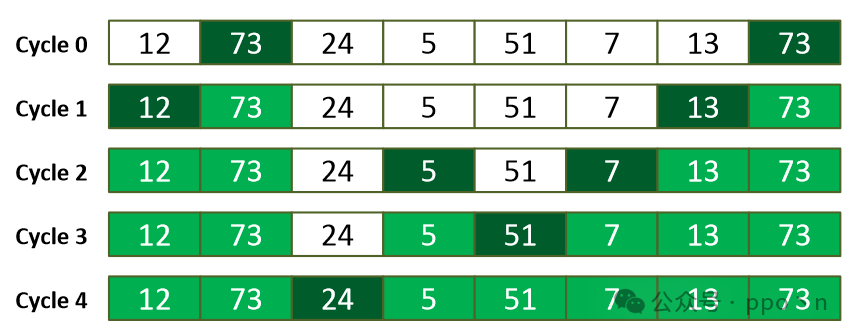
Of course, this method also has certain overheads:

• Requires additional hardware to check and record this potential spatial locality
• Accessing the entire cache line may lead to increased power consumption, etc.
• Increases the complexity of the interconnect from core to cache, as each element extracted from the cache line needs to be accessed by all SIMD elements.
• The instruction scheduler may need to predict access cycles and be able to recover in case of prediction errors

Memory System Support

Here we only focus on the first level of the memory system.

For TLB, the issues encountered are similar to those of cache, but there is less need to consider consistency maintenance, so TLB can be simply replicated. Another option is for gather and scatter instructions to skip address translation directly, but this usually requires that the address space used is different from the different memory spaces, such as software-managed scratchpad cache. This method has been widely used in GPUs, such as shared memory.

For DCache access:

• Increase the number of data elements that can be accessed between the core and cache
• Must be greater than SIMD width, otherwise it cannot meet the requirement of executing a computation instruction per cycle for SIMD
• Increase the number of data elements that can be read/written from the data array
• Organize the data array into multiple independently controlled banks, allowing different cache line accesses to occur simultaneously on different banks

The figure below is an example where each cycle supports access to 4 elements, with each cache line split across banks. Each bank is independently controlled and has a Tag, allowing simultaneous access to different cache lines. If accessing the same bank, it will lead to<span>bank conflict</span>.

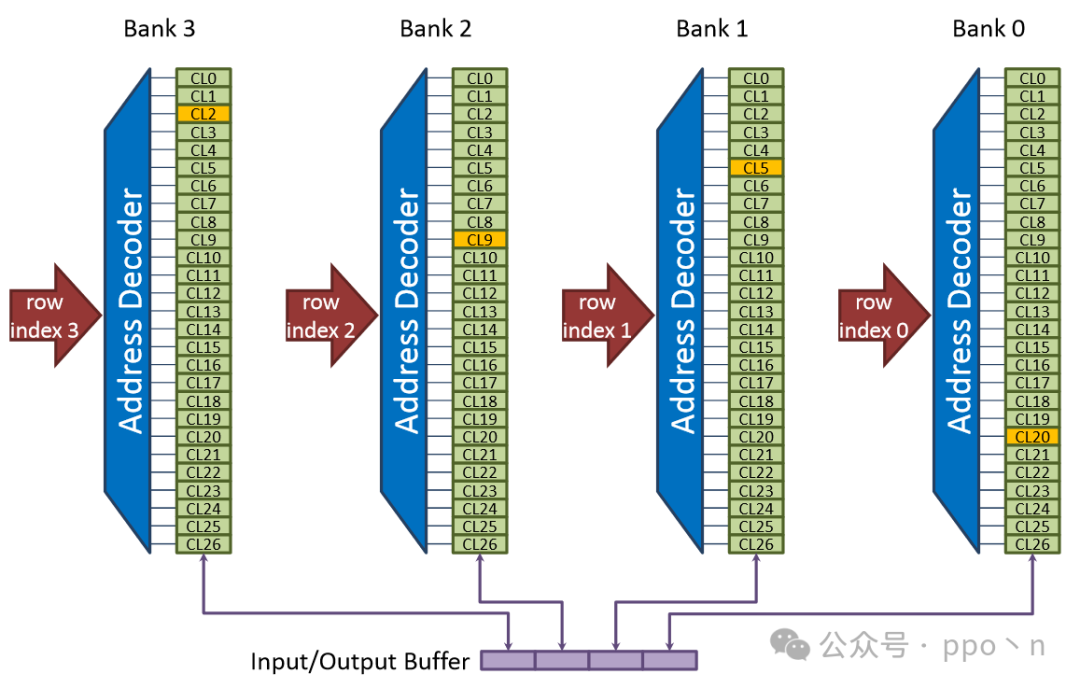
The figure below shows the expected memory access cycles for gather/scatter instructions under different SIMD widths and bank numbers, assuming each bank has only one port and all banks have the same access probability. It can be seen that the larger the SIMD width, the higher the probability of bank conflicts.

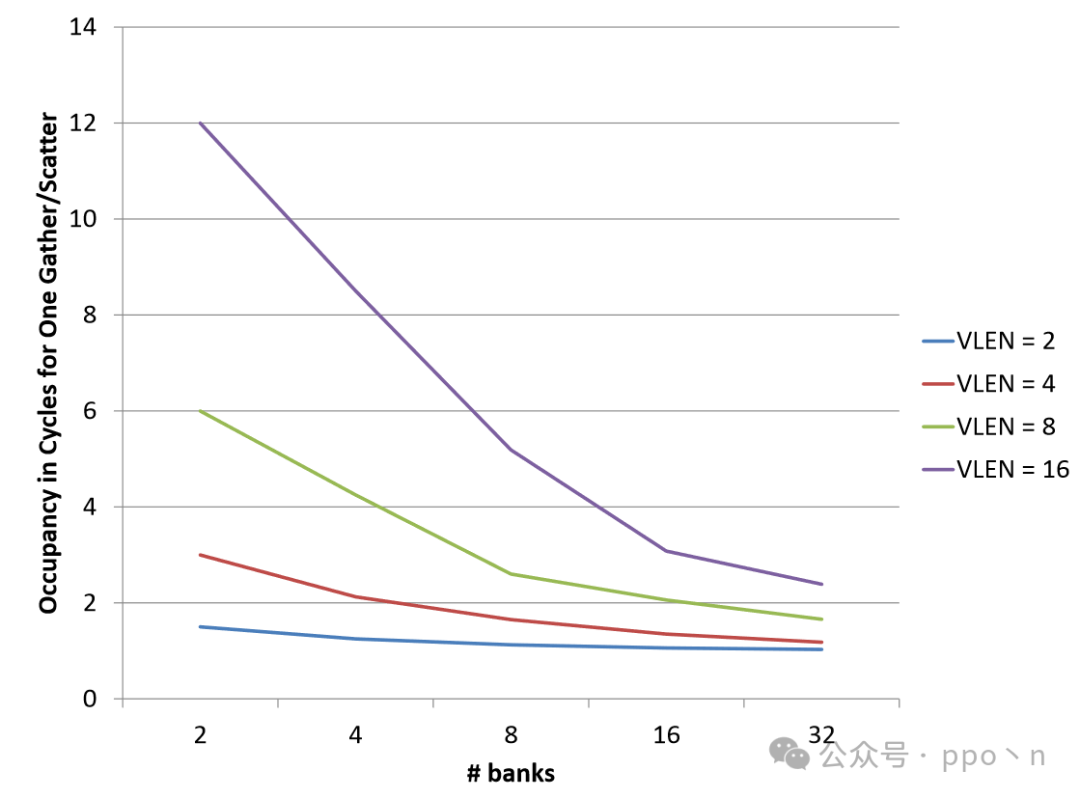
Additionally, for some special applications, such as memory access scenarios with stride patterns (which can be mitigated through random padding or hashing), the occurrence of bank conflicts will be exacerbated. Another drawback is that this method requires a lot of additional hardware, including checks for bank conflicts, duplicated logic between different banks, etc.

In particular, the arrangement of data between banks can have different organizational forms, depending on the specific implementation, with classic interleaved arrangements between banks. Besides banked caches, additional buffers or even software-managed buffers can be considered to resolve issues.

4.2.3 Locality of Gather and Scatter

No Locality Computation

When using SIMD to perform lookups in large hash tables or traversing large binary search trees, locality is rarely observed, putting significant pressure on the memory system. In this case, it may be better to bypass the cache and request the smallest possible blocks from main memory.

Locality Computation

When programs indirectly access small data structures, such as accessing small lookup tables (function approximations) related to input entries, they exhibit temporal locality. Some sparse matrix computations also involve locality.

Similarly, for some small datasets that may be reused, spatial locality will be present.

A typical example is shown below, where the input data structure is AoS (Array of Structure) with 4 fields.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
  X[i] = A[B[i]].x; 
  Y[i] = A[B[i]].y; 
  Z[i] = A[B[i]].z; 
  W[i] = A[B[i]].w; 
} 

// Vectorized loop with gathers 
for (i = 0; i < N; i += VLEN) 
{ 
vload v0, B[i] 
vload v1, B[i] 
vload v2, B[i] 
vload v3, B[i] 
vstore X, v1 
vstore Y, v2 
vstore Z, v3 
vstore W, v4 
}

The figure below illustrates the AoS-to-SoA structure, assuming a SIMD width of 2, where elements in B alternate between 0/7. Thus, the first extraction retrieves x0/x7, the second retrieves y0/y7, and so on.

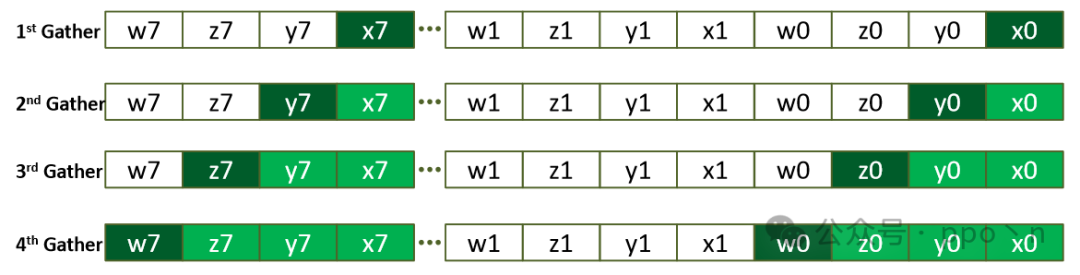
5. Horizontal Operations

While SIMD execution has been fully discussed, hardware treats vector elements as completely independent. However, actual computations also involve dependencies or calculations between different data elements within the same vector, requiring additional mechanisms to pass information from one element to another or to merge elements.

Intuitively, this can be achieved through memory, utilizing unaligned data access gather/scatter combined with appropriate operations, but with lower efficiency. Generally, dedicated hardware circuits are designed to perform these<span>horizontal operations</span>, including:

• Data movement instructions
• Reduction instructions
• Using horizontal instructions to assist with control divergence
• Handling dependencies between elements within vectors that can only be monitored dynamically

5.1 Limitations of Horizontal Operations

The cost of horizontal operations mainly lies in data redistribution. If arbitrary redistribution within the vector is allowed, its cost is quadratic in relation to vector length. Therefore, many real hardware designs either implement multi-level networks to achieve data distribution, which may increase latency, or impose some restrictions on data distribution, such as only allowing redistribution of specific and regular data within the vector.

5.2 Data Movement

Basic data movement operations can be categorized based on input:

• Broadcast
• The input is a single value, which is copied to all output elements
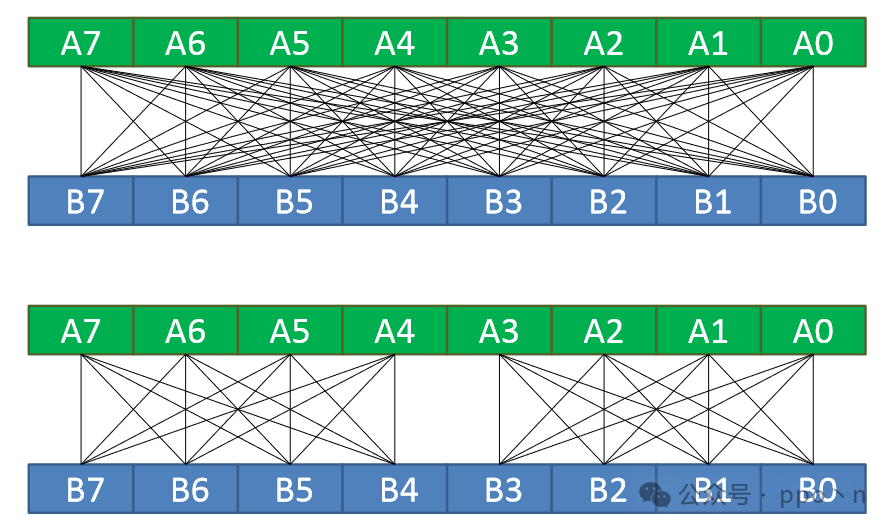
• Permute
• The input is a vector, allowing software to select any element within the vector for input and output to any element
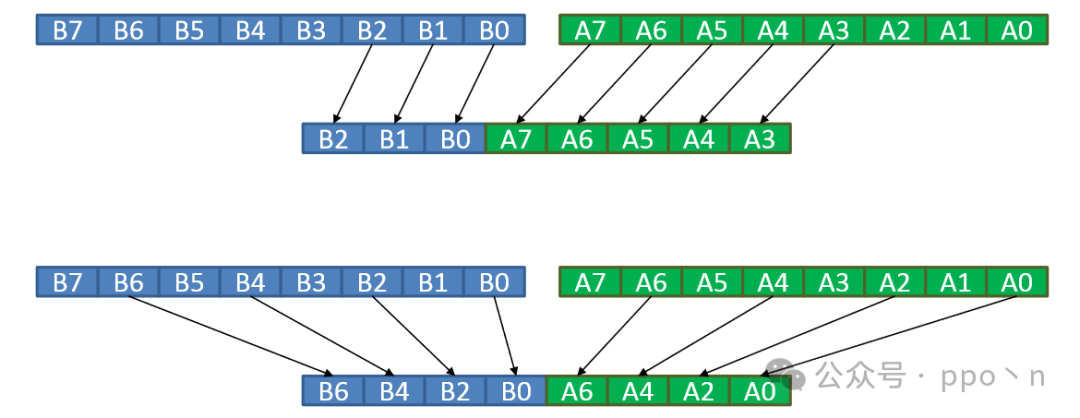
• Shuffle
• The input is multiple vectors, similar to permute, but operates on two or more vectors

The figure below illustrates an example of permute, where the top shows unrestricted arbitrary allocation, while the bottom shows restricted allocation, dividing it into two groups, allowing only allocation within the group.

The figure below shows examples of two shuffle operations, where the top selects consecutive elements from two vectors to output to a new vector, which is useful for operations like filters requiring sliding windows, while the bottom removes even elements from two vectors, applicable for AoS structure operations, belonging to stride types.

Regarding software selection for data movement operations:

• Built-in
• The instruction definition includes the exact data movement method
• Scalar value
• The instruction can take a scalar value as a parameter, which can be an immediate value or a scalar register
• Vector of value
• The instruction takes a vector value as a parameter, which is more flexible, and can be an immediate value, scalar register, or vector register.

Data movement operations are typically used to reorganize data structures or reorder elements within vectors to meet data dependencies, as well as to implement efficient lookup tables. For example, if the entire table can fit into SIMD registers and the indices of the required elements are placed in another SIMD register, executing a permute operation is equivalent to performing a table lookup, which is very efficient.

The last two types of data movement operations are<span>compress</span> and <span>expand</span>, which, compared to previous operations, require implicit communication between different vector elements to determine the correct output positions. The figure below illustrates this.

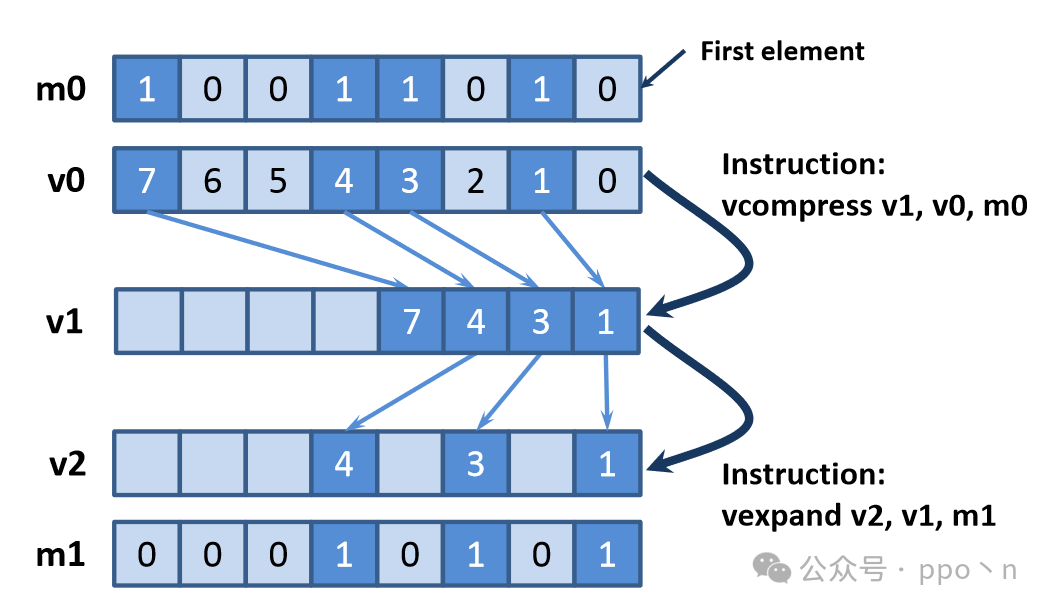
5.3 Reduction

Reduction operations take a set of data and combine them to produce fewer data. For single-threaded code, software is typically used to compute the sum of a set of elements. A SIMD execution method is shown in the figure below, performed in a binary tree form.

This method is not very efficient and requires serial execution. Dedicated hardware can also complete the instruction, but the overhead is not low, requiring specific trade-offs.

5.4 Reducing Control Divergence

This section introduces how to use horizontal operations and gather/scatter operations to reduce control divergence. A common approach is to add preprocessing steps before divergence occurs, making the data structure more convenient for the SIMD model to execute, mainly based on some hardware-assisted software strategies.

Another recently popular method is<span>automatic regrouping</span>, which has no side effects on software and is currently mainly applied to architectures with implicit masking capabilities.

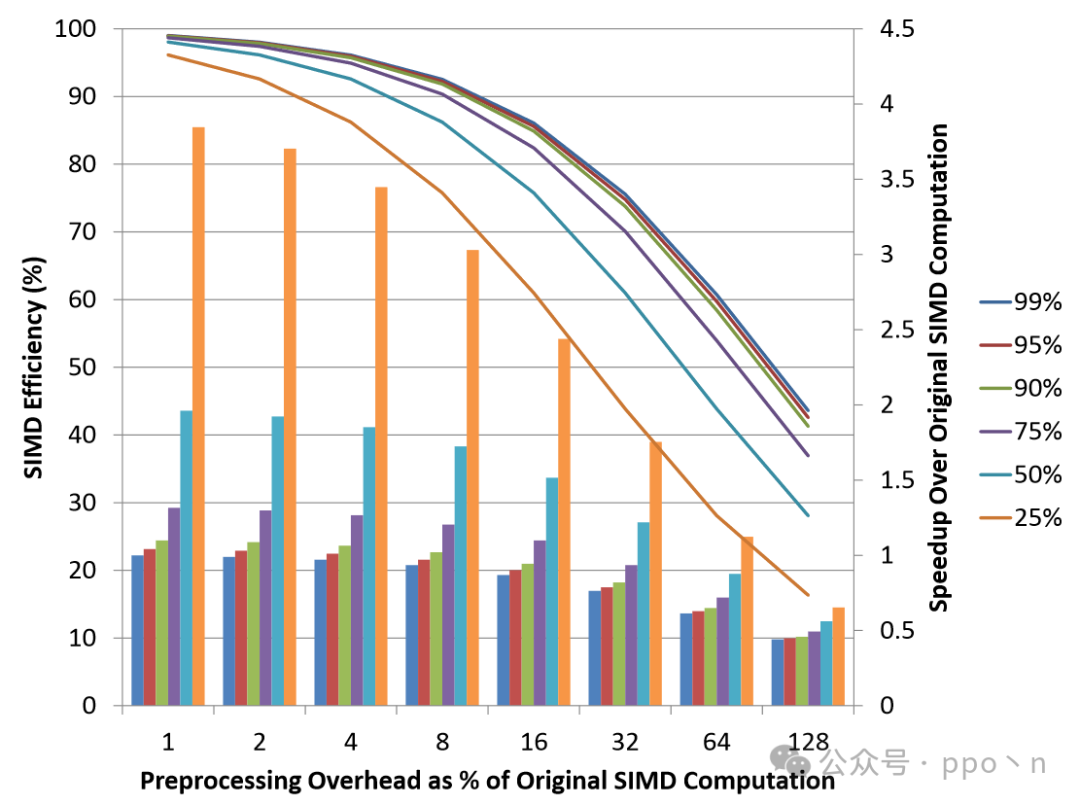
Quantifying the Benefits of Regrouping

The figure below assumes perfect regrouping, displaying the results of SIMD efficiency as a line and the speedup compared to the original code as a bar chart. Different colors represent the SIMD Efficiency of the original code.

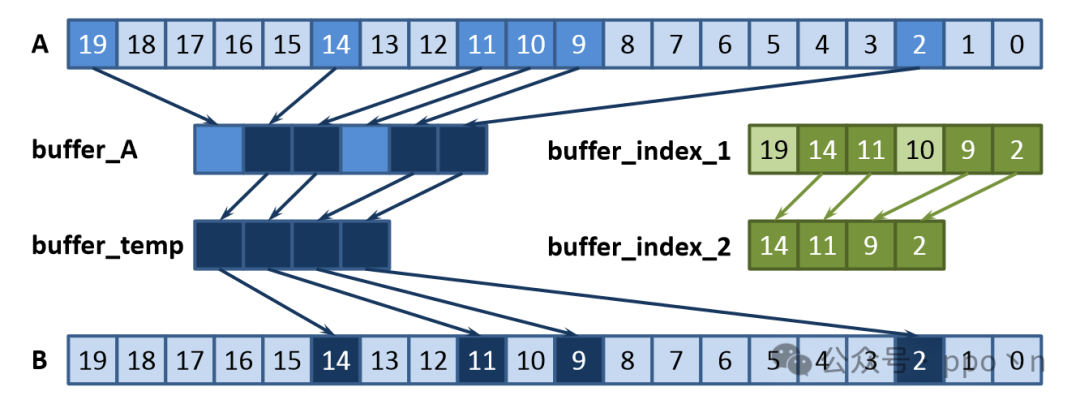
Nesting Control Flow and Regrouping

The code for nested control flow is as follows.

for (i = 0; i < N; i++) 
{ 
  if (A[i] > 0) 
  { 
    temp = A[i] & bit_mask; 
    
    if (temp > constant) 
    { 
      B[i] = -temp; 
    } 
  } 
}

Two-level regrouping can be used to solve this, as shown in the figure below, where the darker blocks indicate blocks that satisfy the corresponding if conditions.

Reducing Regrouping Overhead

The main overhead of regrouping comes from transferring the data that meets the conditions into/out of contiguous buffers, which can be directly achieved using SIMD operations, as shown below.

for (i = 0; i < N; i += VLEN) 
{ 
vload v3, A[i] 
vcmpgt m0, v3, v0 // v0 contains all zeros 
vcompress v4, m0, v2 
vstore buffer_index[num_elements], v4 
  
  num_elements += popcnt(m0); 
vadd v2, v2, v1 
}

Another overhead is the space required to store compressed indices. A method that only requires at most twice the number of elements in the vector for the buffer is to immediately perform the corresponding consuming operations after generating the index buffer, which can significantly reduce the demand for buffer capacity.

5.5 Potential Dependencies

SIMD’s horizontal data movement and reduction instructions allow software to satisfy known data dependencies within vectors. However, some computations have unpredictable dependencies, meaning that software does not know at compile time whether dependencies exist, only that they may exist. This situation is most common in indirect memory operations, where the pattern is not static. Such potential dependencies may prevent vectorization.

The following shows a classic example, histogram computation.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
  bin = A[i]; 
  histogram[bin]++; 
} 

// Incorrectly vectorized loop 
for (i = 0; i < N; i+=VLEN) 
{ 
vload v0, A[i] 
vgather v1, histogram, v0 
vadd v1, v1, v2 // v2 is {1, 1, ..., 1} 
vscatter histogram, v0, v1 
}

In the incorrectly vectorized program shown below, the bottom shows the scalar computation results. The same elements within the vector will only compute the histogram once, leading to incorrect results.

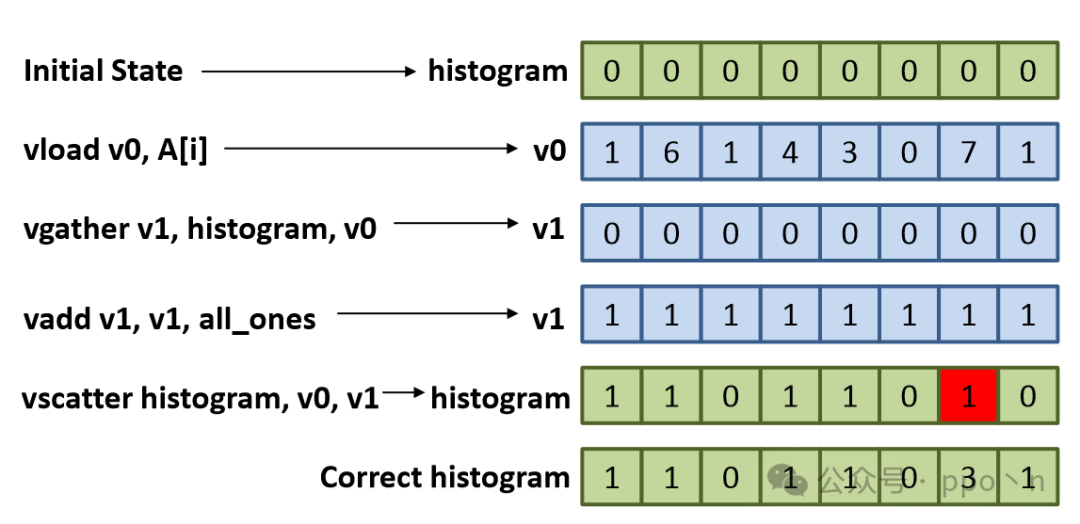
The fundamental reason at the lowest level is that there is a RAW dependency in the scalar program, meaning that after the previous histogram statistic is completed, it needs to read the original value before performing the next accumulation, and whether a dependency occurs depends on the specific values.

5.5.1 Single-index Case

Checking Conflicts

First, consider the situations in which the above dependency occurs under different conditions, as shown in the figure below, where solid lines represent the conflict fraction within the SIMD vector, and dashed lines represent the frequency of the maximum same values within the vector. It can be seen that when the array size is large, the probability of the above dependency occurring is low, indicating the feasibility of using specific mechanisms to check dependencies to improve execution efficiency.

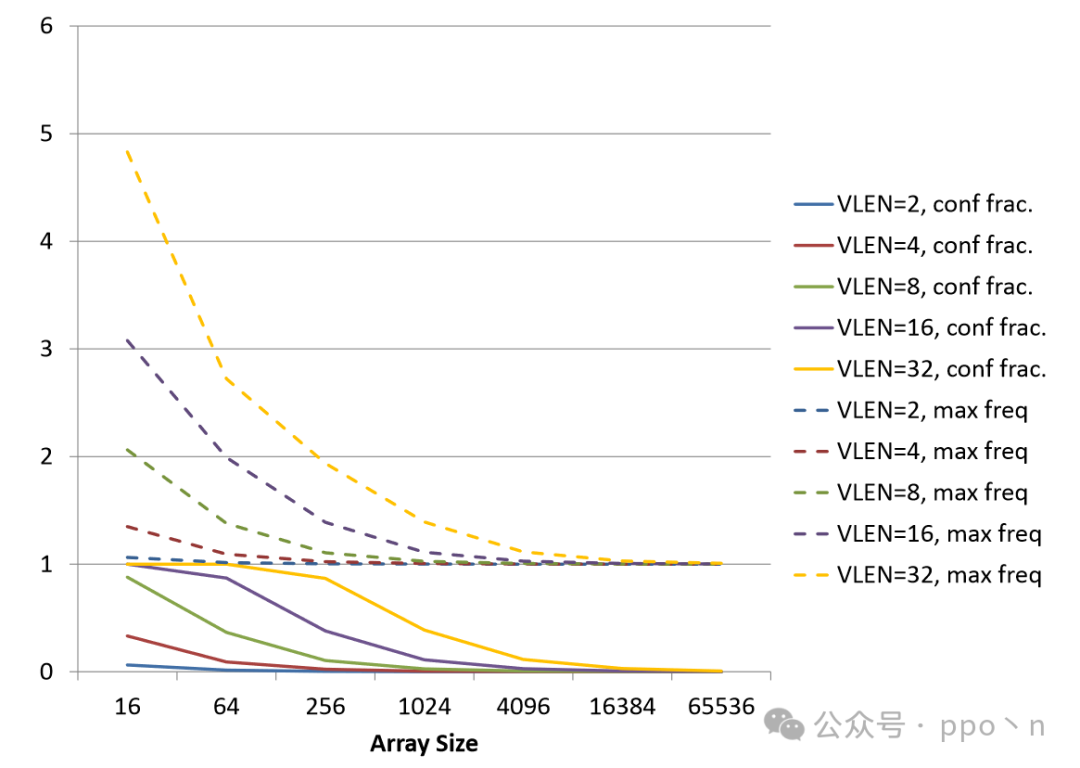
On one hand, dependencies can be checked in advance using scalar or vector methods, executing only the parts without dependencies using SIMD, as shown in the two codes below.

// scalar
for (i = 0; i < VLEN; i++) 
{ 
for (j = 0; j < i; j++) 
  { 
if (index[i] == index[j]) 
returntrue; 
  } 
}

//vector
// v0 = indices to test 
for (i = 0; i < VLEN; i++) 
{ 
vbroadcast v1, v0, i 
vcmpeq m0, v0, v1 

if((m0 & ~(1 << i) != 0))// check for match besides self-match 
returntrue; 
}

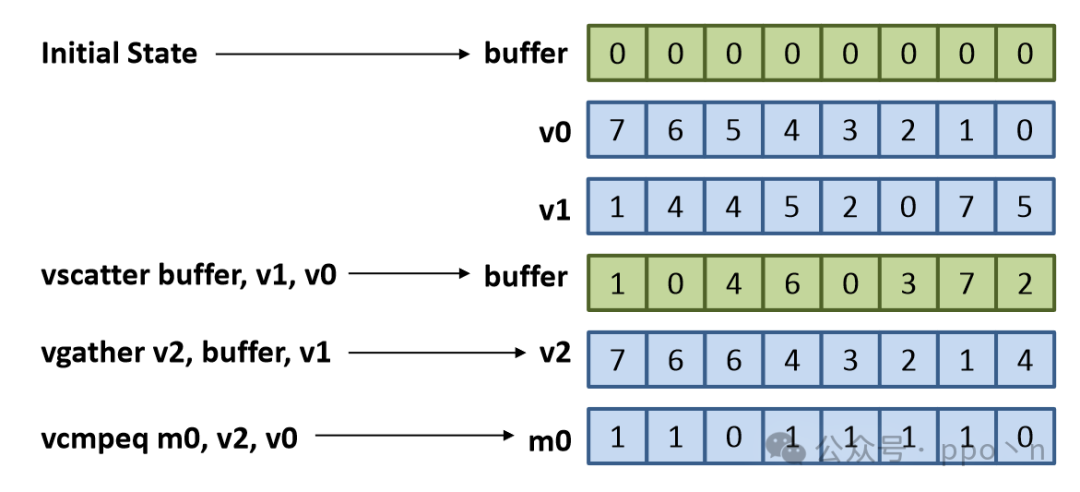
Another approach is to use scatter and gather instructions, as shown below.

// v0 = {0, 1, ..., VLEN-1} 
// v1 = indices to test 
vscatter buffer, v1, v0 
vgather v2, buffer, v1 
vcmpeq m0, v2, v0 
if (m0 != all_ones) 
  return true;

Scalar Execution

A simple and direct method is to execute the code that checks for dependencies using scalar methods. The figure below shows the SIMD efficiency when reverting to scalar execution upon encountering conflicts. Here, it is assumed that the vector length is 16, with the dashed line indicating checking conflicts with 1 instruction, and the solid line indicating checking conflicts with 32 instructions. This method limits efficiency to below.

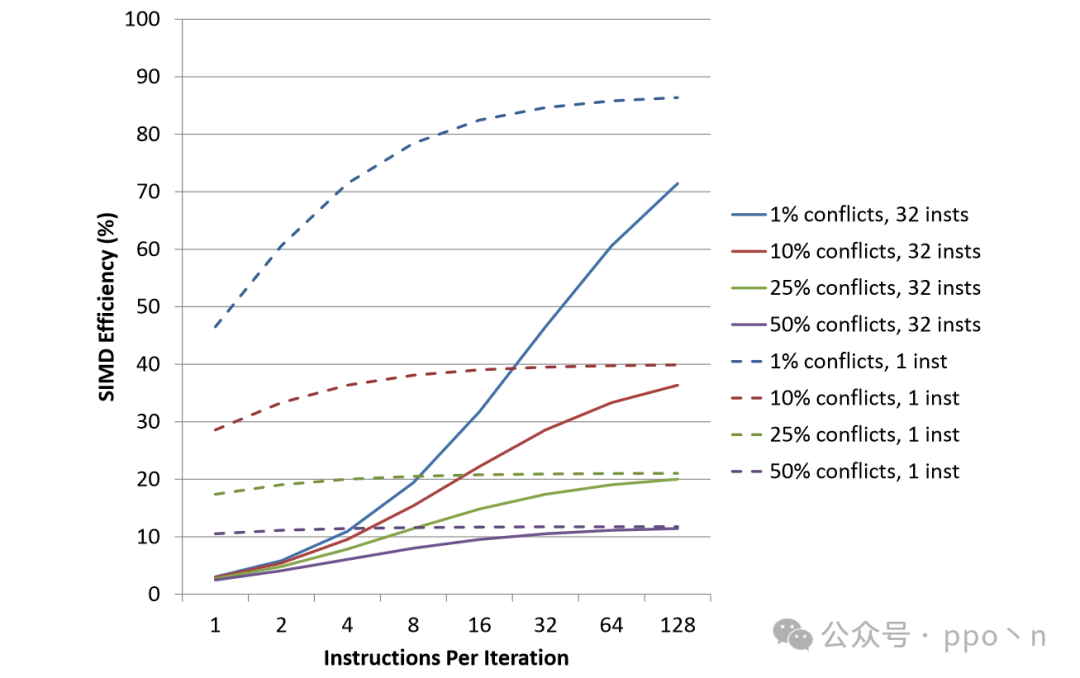
It can be seen that unless the conflict probability is very low, this method has a significant impact on performance.

SIMD Execution

When conflicts exist, SIMD execution can be represented as:

1. Initialize vector elements V
2. Find the largest conflict-free set from V
3. Perform SIMD computations on the data in 2
4. Remove data from 2, and if V is still non-empty, repeat execution

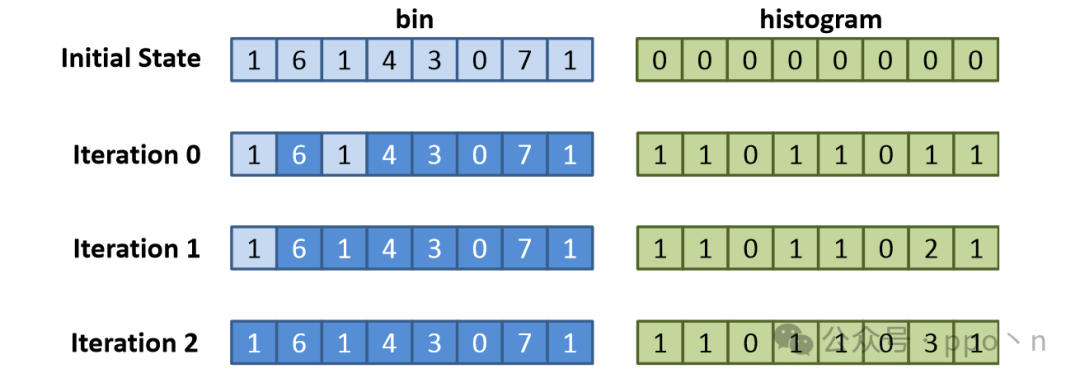
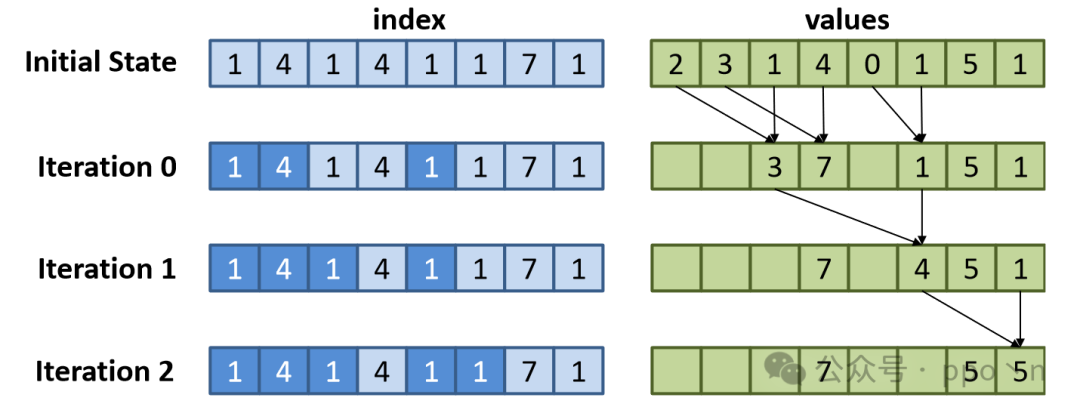
The figure below shows an example execution of the histogram code, which matches the scalar execution results.

A more optimal method is to use a tree reduction method:

1. Initialize vector elements V
2. Pair duplicate indices, recording and removing unique indices (which are the roots of the reduction tree)
3. Perform SIMD execution on the elements in each pair
4. Remove one element from each pair in V, and if V is non-empty, repeat
5. Only use root elements to perform gather-update-scatter

The figure below shows an example where the right-side values are added according to the memory positions indicated on the left. This method only requires

5.5.2 Multi-index Case

When multiple indices exist for the same array, the situation becomes particularly complex, especially during detection. The following is an example.

// Scalar loop 
for (i = 0; i < N; i++) 
{ 
  A[B[i]] = A[C[i]]; 
} 

// Incorrectly vectorized loop 
for (i = 0; i < N; i += VLEN) 
{ 
vload v0, B[i] 
vload v1, C[i] 
vgather v2, A, v1 
vscatter A, v0, v2 
}

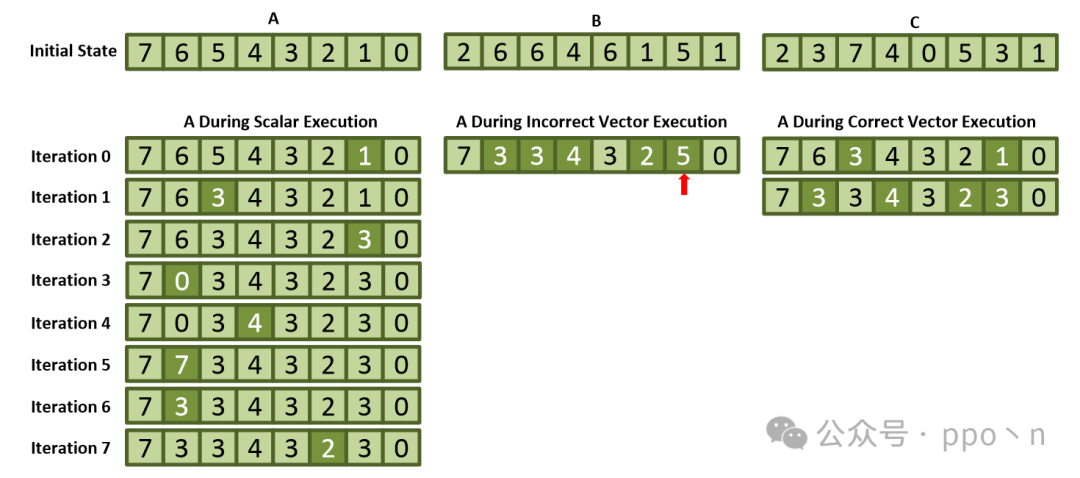
The error in the figure arises from the dependencies present in column A[1], and there are also hidden dependencies in A[6], but these are not considered here. To check for this type of conflict, it is necessary to determine whether there are duplicates among all index vectors or whether there are RAW dependencies.