Source: “China Electric Power”, 2024, Issue 1
Citation: Zhang Chao, Zhao Dongmei, Ji Yu, et al. Real-time Optimization Scheduling of Virtual Power Plants Based on Improved Deep Q-Networks [J]. China Electric Power, 2024, 57(1): 91-100.
Click the “Read the original text” button at the bottom left corner of the article to view the full paper on your mobile device. Log in to the official website www.electricpower.com.cn to download the full text for free.
Editor’s Note
In the context of new power systems, the large-scale integration of renewable energy into the grid presents significant challenges due to its randomness and volatility. To address this issue, the Virtual Power Plant (VPP) integrates renewable energy, energy storage, and load devices through intelligent control technology, seeking optimal scheduling strategies for dispatchable resources through energy management. The first issue of “China Electric Power” in 2024 published the article “Real-time Optimization Scheduling of Virtual Power Plants Based on Improved Deep Q-Networks” written by Zhang Chao et al. This article proposes an improved DQN algorithm (improved deep Q-network, MDQN) applied to the real-time optimization scheduling of VPPs under a cloud-edge collaborative architecture based on deep reinforcement learning. The MDQN algorithm strictly adheres to all operational constraints in the action space, ensuring that the scheduling plan formulated is feasible during real-time operation. This paper also conducts a comprehensive comparison of the performance of the MDQN algorithm with other DRL algorithms (such as DDPG, SAC, and TD3 algorithms) to highlight its superior performance advantages.
Abstract
Deep reinforcement learning algorithms are data-driven and do not rely on specific models, effectively addressing the complexity issues in the operation of virtual power plants. However, existing algorithms struggle to strictly enforce operational constraints, limiting their application in real systems. To overcome this issue, an improved deep Q-network (MDQN) algorithm based on deep reinforcement learning is proposed. This algorithm expresses deep neural networks as mixed-integer programming formulations to ensure strict enforcement of all operational constraints within the action space, thereby guaranteeing the feasibility of the scheduling in actual operations. Additionally, sensitivity analysis is conducted to flexibly adjust hyperparameters, providing greater flexibility for algorithm optimization. Finally, comparative experiments validate the superior performance of the MDQN algorithm. This algorithm provides an effective solution to the complexity issues in the operation of virtual power plants.01
Cloud-edge Collaborative Control Technology
1.1 Cloud-edge Collaborative Control Architecture
In the cloud-edge collaborative architecture, the communication, dynamic allocation of data, and business resources between the cloud and edge layers are key elements. Through dynamic allocation, the cloud and edge layers can achieve bidirectional data transmission from bottom to top and top to bottom, completing the collaborative instructions for business and application services (see Figure 1). This bidirectional data transmission mechanism allows the cloud and edge layers to share information in real-time and adjust and optimize as needed.
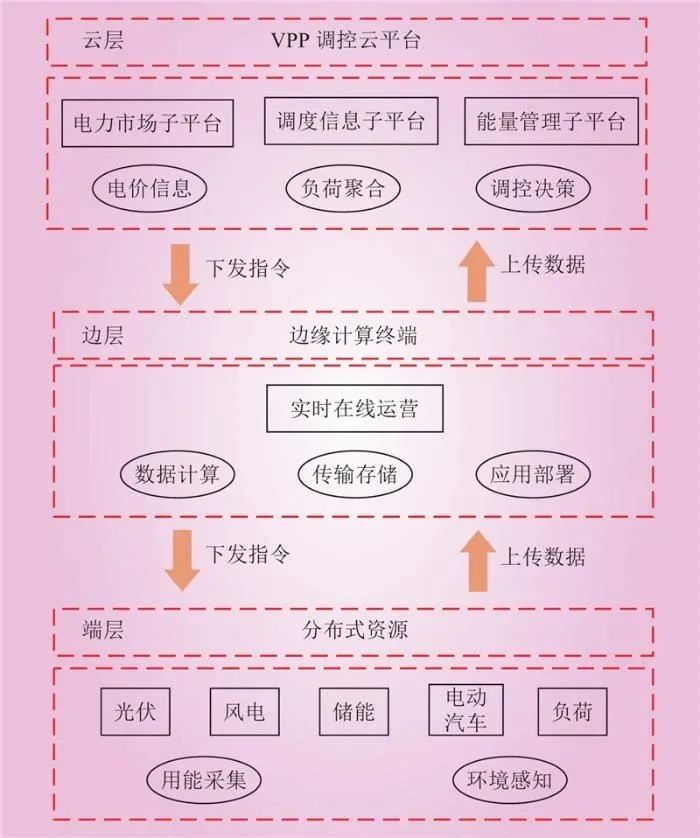
Figure 1 VPP Cloud-edge Collaborative ArchitectureFig.1 VPP Cloud-edge Collaborative Architecture The VPP cloud platform is the core component of the entire virtual power plant. The power market sub-platform is responsible for participating in power market transactions as a bidder and publishing market clearing results. The scheduling information sub-platform manages the control information and characteristics of sources, networks, loads, and storage, ensuring that the operation of the VPP meets system requirements. The energy management sub-platform is responsible for controlling and monitoring users within the VPP to achieve effective management and distribution of energy. Edge computing terminals play a role in real-time online operations. These terminals are responsible for data collection and aggregation, utilizing models obtained during the offline training phase for real-time online scheduling. By performing real-time scheduling on edge computing terminals, communication delays with the cloud platform can be reduced, improving decision-making speed and real-time performance. Additionally, the edge layer is a collection of various distributed resources and electrical devices within the virtual power plant. These devices are responsible for uploading operational information in real-time and receiving control instructions from the control cloud platform or edge computing terminals. Through real-time feedback and response from the edge layer, the entire virtual power plant can achieve coordinated operation and optimization.1.2 Interaction Mode of Cloud-edge Collaboration In the cloud-edge collaborative architecture of the virtual power plant, intelligent algorithms such as deep learning, neural networks, and reinforcement learning are employed. The control cloud platform is the core of the VPP, and its logic is shown in Figure 2.
Figure 2 VPP Control Cloud Platform LogicFig.2 VPP Regulation Cloud Platform Logic Diagram Deep reinforcement learning is applied to the offline training and real-time online scheduling of virtual power plants. In the offline training phase, industrial servers and power servers are responsible for processing and collecting information from the generation side and user side in specific areas, transmitting the collected information to the VPP control cloud platform. The cloud platform utilizes this large-scale offline data for training, optimizing scheduling strategies through deep reinforcement learning algorithms. After training is completed, the trained model is transmitted to the edge computing terminals in specific areas. Due to the large number of users in the virtual power plant and the requirement for real-time demand response, both servers transmit the collected real-time data to the edge computing terminals. The edge proxy terminal utilizes the previously trained model, inputs the real-time data into the model, and generates real-time economic scheduling strategies through deep reinforcement learning algorithms.
This cloud-edge collaborative architecture based on deep reinforcement learning provides efficient decision support for the operation of virtual power plants, making the scheduling and resource management of VPPs more intelligent.
02
VPP Real-time Optimization Scheduling Model
The VPP structure considered is shown in Figure 3, which includes various distributed resources such as solar photovoltaic, energy storage stations, micro gas turbines, and loads. These resources are connected to the public grid and participate in power market transactions to maximize benefits, with the objective function aimed at reducing the overall operational costs of the VPP.
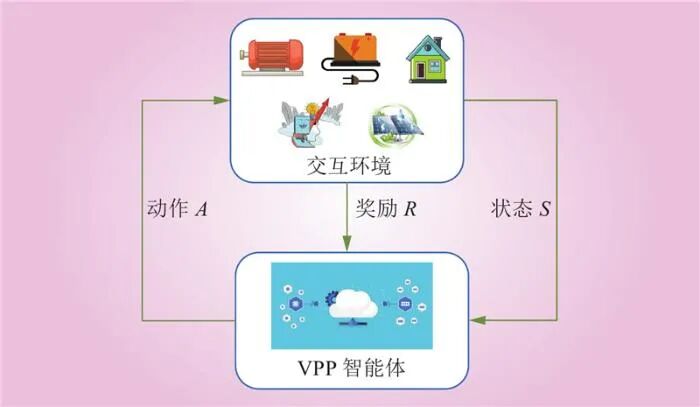
Figure 3 VPP Structural FrameworkFig.3 VPP Structural Framework2.1 Objective Function The objective function can be expressed as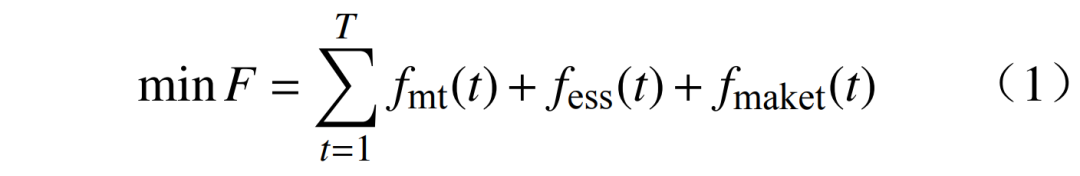 
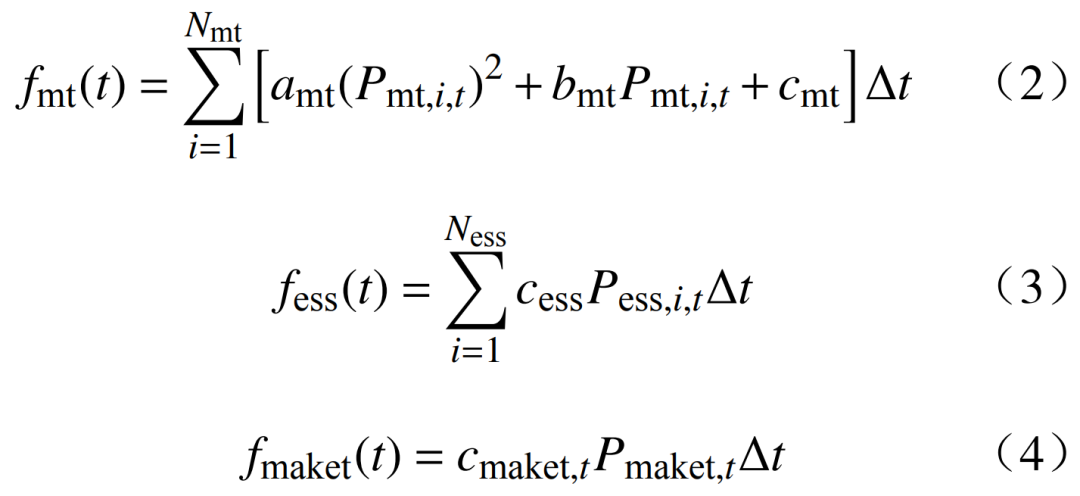where: fmt(t), fess(t), fmaket(t) represent the costs of the micro gas turbine, energy storage, and power market transactions at time t, respectively; Nmt, Ness are the numbers of micro gas turbines and energy storage units, respectively; Pmt,i,t is the power output of the i-th micro gas turbine at time t; amt, bmt, cmt are the cost coefficients of the micro gas turbines; Pess,i,t is the charging and discharging power of the i-th energy storage unit at time t; cess is the cost coefficient for charging and discharging of the energy storage unit; cmaket,t is the electricity price in the power market at time t; Pmaket,t is the trading power in the power market at time t.2.2 Constraints 1) Power balance constraint is 
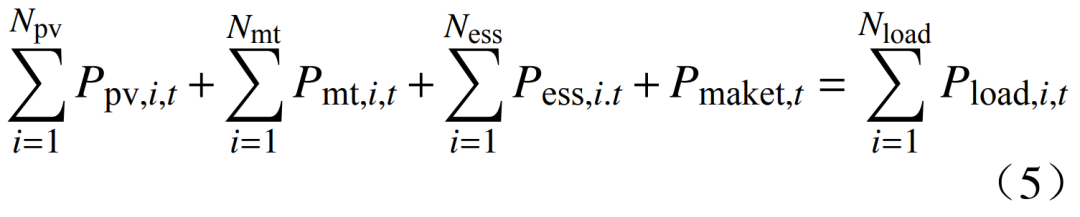where: Ppv,i,t is the power output of the i-th photovoltaic unit at time t; Pload,i,t is the power of the i-th load at time t; Npv, Nload are the numbers of photovoltaic units and loads, respectively. 2) Micro gas turbine operation constraints: ① The output constraint of the micro gas turbine is 
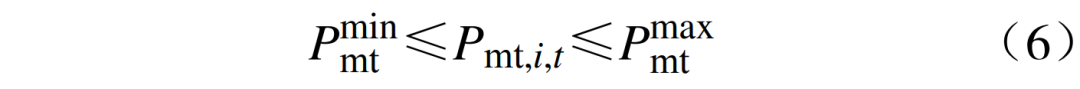where: 
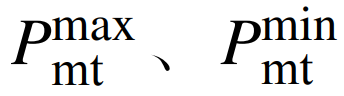are the upper and lower limits of the micro gas turbine output. ② The ramp rate constraint of the micro gas turbine output is 
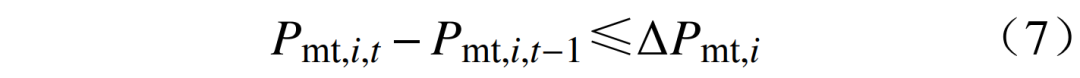where: 
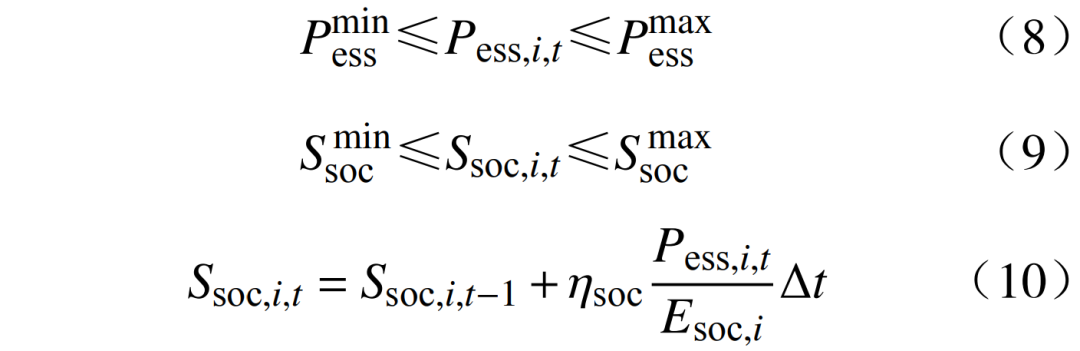where: 
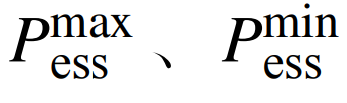are the upper and lower limits of the charging and discharging power; Ssoc,i,t is the state of charge of the energy storage; 
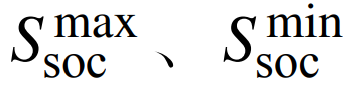are the upper and lower limits of the state of charge of the energy storage; ηsoc is the charging and discharging efficiency of the energy storage unit; Esoc,i is the capacity of the energy storage station. 4) Interaction power constraints are 
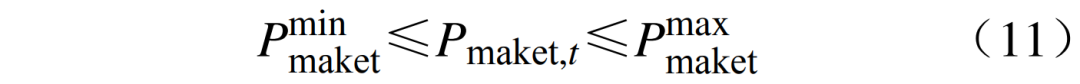where: 
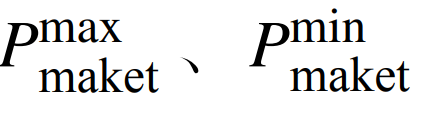are the upper and lower limits of the VPP interaction power.03
Markov Decision Process (MDP) Modeling
The Markov decision process (MDP) provides a mathematical framework for decision modeling, which can be represented as a five-tuple:
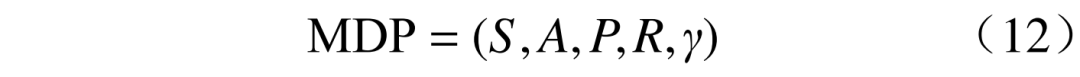where: S is the state space; A is the action space; P is the state transition probability, describing the probability of the environment transitioning from one state to another, directly obtaining experience data through interaction with the environment in model-free algorithms; R is the reward function; γ is the discount factor. 3.1 State SpaceS is the set of environmental states observed by the agent, where the environmental state information includes the state of charge of controllable energy storage units, micro gas turbine output, renewable energy output, and load amount. The state space is 
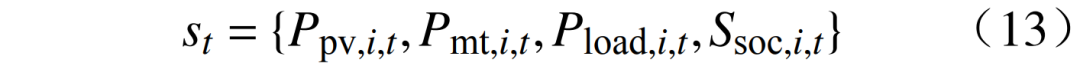3.2 Action Space The action set A is represented by a series of action variables, with the system’s decision variables being 
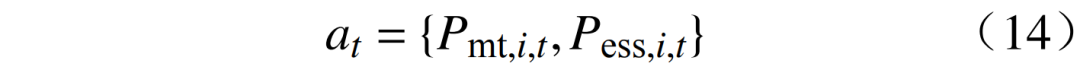3.3 Reward Function The reward function R guides the agent to take actions that minimize total operating costs while satisfying power balance constraints. The reward function is 
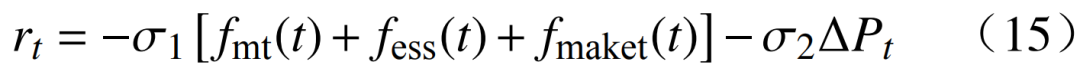where:
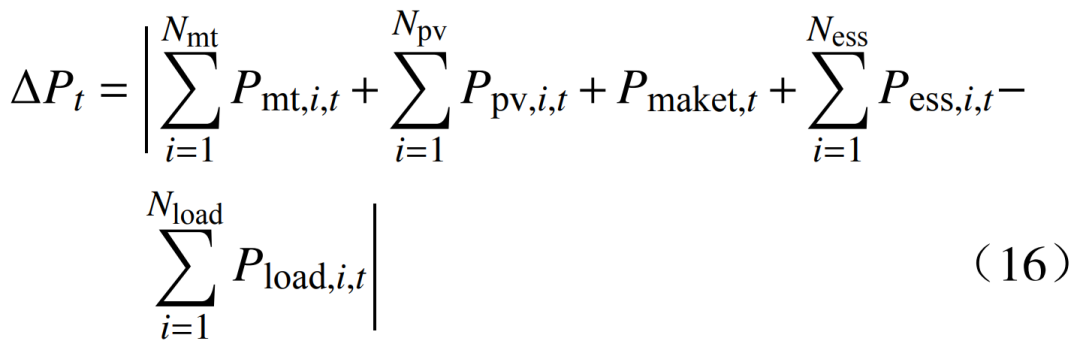
04
Improved DQN Algorithm (MDQN)
DQN is a deep learning-based Q-learning algorithm that primarily combines value function approximation with deep neural network (DNN) technology, employing target networks and experience replay methods for network training. The Q function can be expressed as
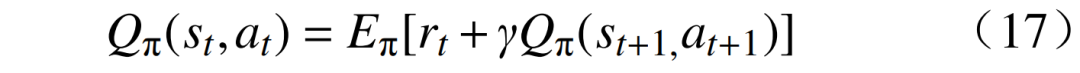The optimal value function of the Q function is 
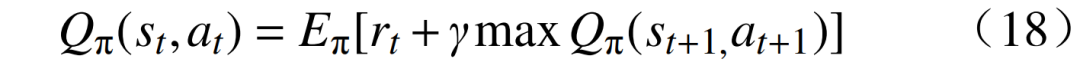The incremental Q value update is performed using temporal difference learning objectives, i.e., 
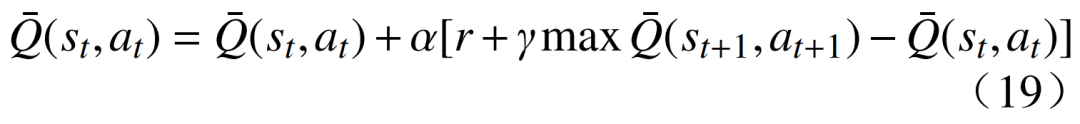where: 
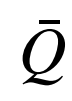is the function approximator; α ∈(0,1] is the learning rate. By 
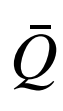obtaining 
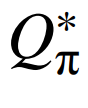high-quality representations, under state st, optimal actions at can be sampled from the optimal policy π*(st), i.e., 
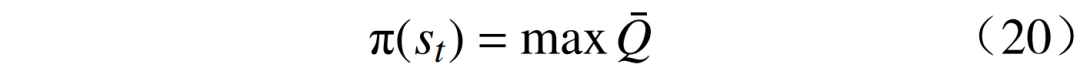For continuous state and action spaces, the optimal action value function 
can be approximated using DNN, i.e., under parameters θ, 
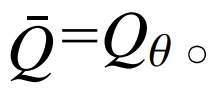In this case, the iterative process shown in equation (19) can be viewed as a regression problem, with the goal of estimating the parameters θ of the DNN through stochastic gradient ascent. In DQN, the value rt + γmaxQθ
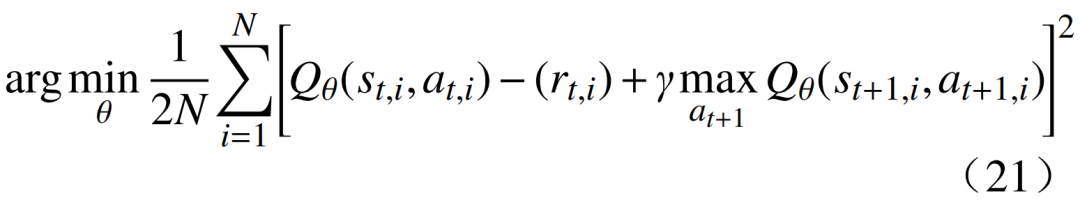In continuous action spaces, the process of sampling actions from the Q function is infeasible, and in equation (20), constraints are completely ignored. To overcome this, the DQN algorithm is combined with mixed-integer programming to form the improved DQN algorithm. The MDQN algorithm is divided into offline training and online execution. The main goal of the training process is to estimate the parameters θ of the deep neural network used to approximate the action value function Qθ; during online execution, the obtained function Qθ is used to specify decisions, directly operating the devices within the VPP. 4.1 Offline Training In traditional value-based reinforcement learning algorithms, actions are typically sampled from the current Q function estimates. However, in continuous action spaces, sampling actions from the action value function Qθ is infeasible. To address this, the MDQN algorithm uses a neural network model for approximation and randomly initializes a deterministic optimal policy
As shown in Figure 4, the DNN Qθ(s,a) consists of K + 1 layers, i.e., layers 0 to K. Layer 0 is the input of the DNN, while layer K is the output of the DNN. Each layer k ∈ {0, 1, ⋯, K} has Uk units, with uj,k representing the j-th unit of layer k. Let xk be the output vector of layer k, then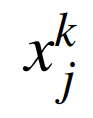 
is the output of the j-th unit of layer k (where j = 1, 2, ···, Uk). Since layer 0 is the input of the DNN, 
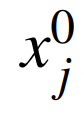is the j-th input value of the DNN. For each layer k ≤ 1, the output vector of unit uj,k is
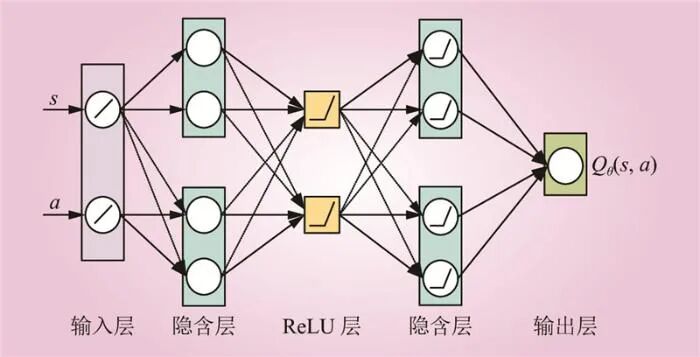
Figure 4 Layer Structure of DNN for Action Value Function Q(s,a)Fig.4 Layer Structure of DNN for Action Value Function Q(s,a)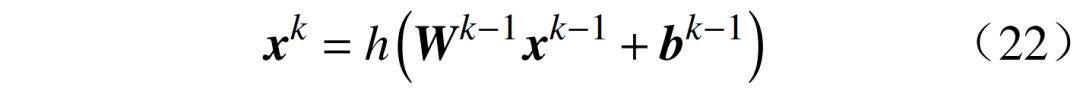
In the equation: 
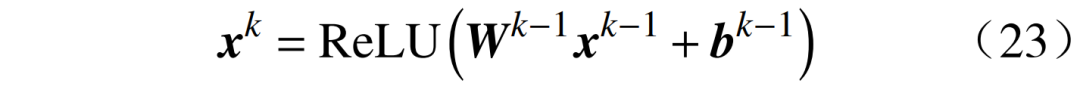Based on the above definitions, the DNN in Figure 4 with fixed parameters θ can be modeled as an effective MIP by using binary constraints to model the ReLU function to solve the problem. Therefore, for each unit uj,k, binary activation variables 
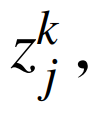are used. The MIP formulation of the DNN can be expressed as 
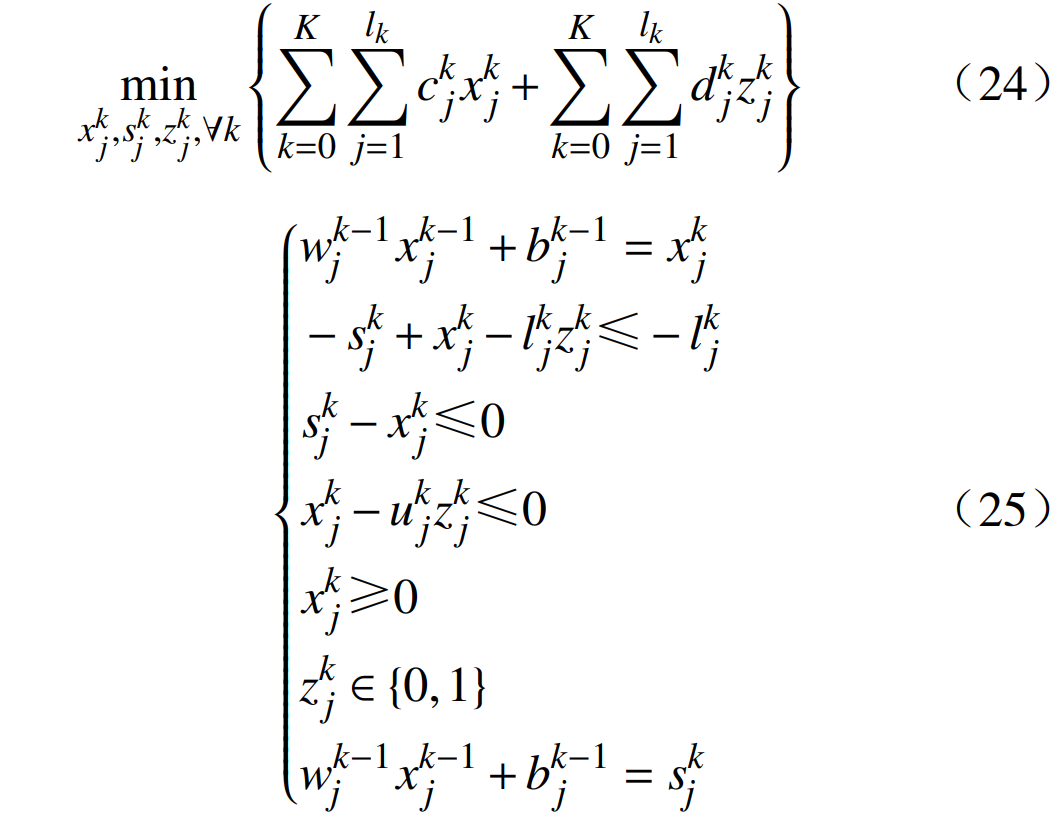where: 
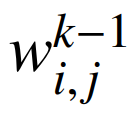are the weights; 
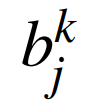are the biases; 
is the objective function cost; 
are the upper and lower limits of x and s.4.2.2 Enforcing Constraints During Online Execution
For any state st, the optimal action at can be obtained by solving the MIP model derived from Qθ in equations (24) and (25). In this case, the decision variable is the action at, and energy balance constraints as well as ramp constraints can be added to describe the MIP model of DNN Qθ. Therefore, the optimal action obtained by solving this MIP model will strictly adhere to all operational constraints in the action space and achieve a globally optimal action selection strategy, thus realizing an effective VPP scheduling strategy.
05
Case Analysis
5.1 Case Parameters
This study conducts case analysis using a virtual power plant that includes photovoltaic, energy storage, and three micro gas turbines. The charging and discharging power limits of the energy storage device are set to 100 kW, with a rated capacity of 500 kW and a charging and discharging efficiency of 0.90. The parameters of the micro gas turbines are detailed in Table 1. A full year of load consumption and photovoltaic generation data is used as the original dataset. To conduct training and testing, the original dataset is divided into two additional datasets for training and testing. The hyperparameters used for all DRL algorithms listed in Table 2 are the same, utilizing Python 3.6 and the deep learning platform Pytorch 1.11.0.
Table 1 Parameters of Each Micro Gas TurbineTable 1 Parameters of Each Micro Gas Turbine
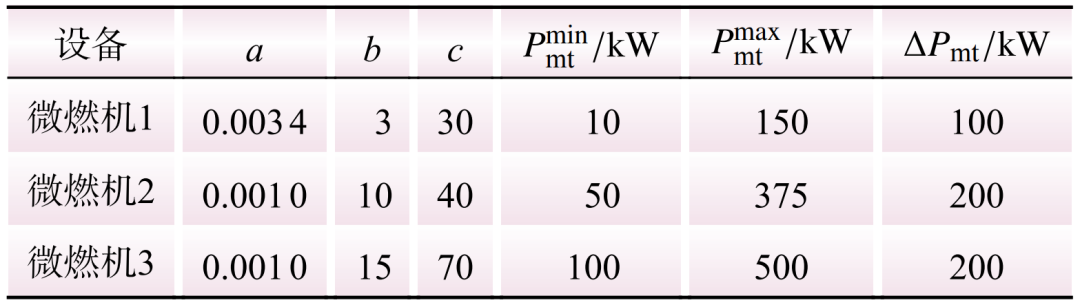
Table 2 Parameters of Each DRL AlgorithmTable 2 Parameters of Each DRL Algorithm
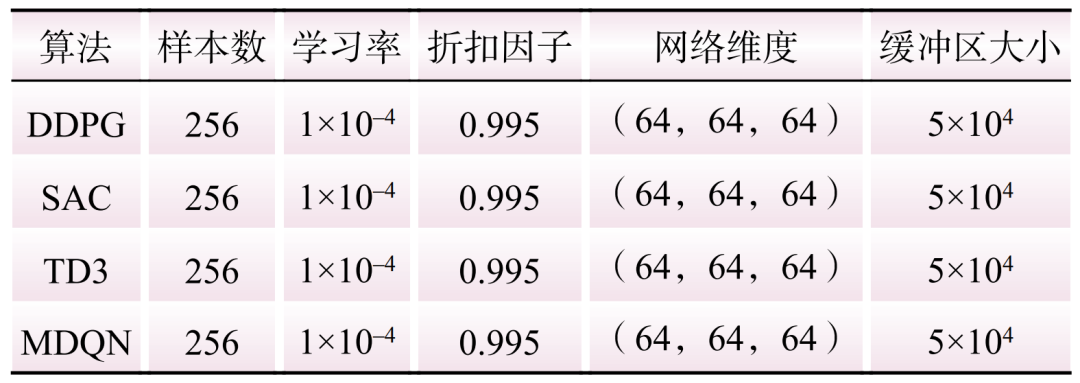
The default values of hyperparameters σ1 and σ2 are 0.01 and 20, respectively. To evaluate the performance of the DRL algorithms, operational costs and power imbalance are used as metrics. 5.2 Offline Training
To verify the performance of the method proposed in this paper, Figure 5 shows the training process of the DDPG, TD3, SAC, and MDQN algorithms, including reward values and power imbalance. From Figure 5, it can be observed that after 50 rounds of training, the average reward value rapidly increases, while the power imbalance significantly decreases. In particular, the MDQN algorithm exhibits more outstanding performance. In the initial stage, the agent is unaware of the environment, and the actions chosen are relatively random, leading to significant fluctuations in reward values. However, with multiple interactions with the environment and accumulation of experience, the parameters of the deep neural network are optimized, leading to better strategy learning. As training progresses, the reward values gradually increase and converge to a stable state.
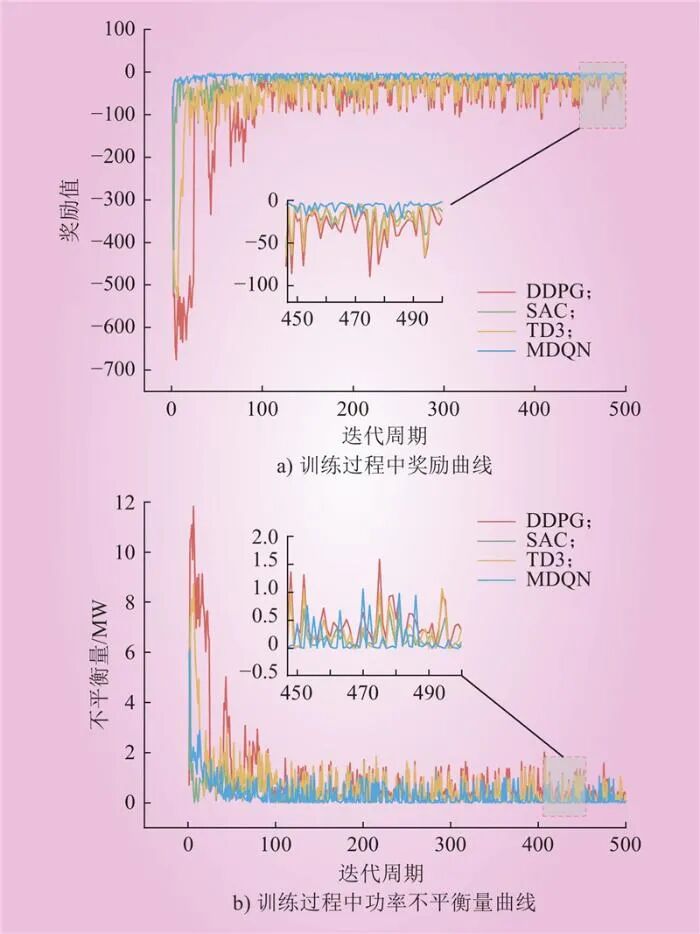
Figure 5 Rewards and Power Imbalance During DDPG, SAC, TD3, MDQN TrainingFig.5 Rewards and Power Imbalance During DDPG, SAC, TD3, MDQN Training Throughout the training process, by introducing penalty terms in the definition of the reward function, the parameters are updated, allowing the agent to select higher-quality actions, reducing power imbalance, and achieving lower operational costs. After 500 rounds of training, all algorithms basically converge, with the final round of training resulting in power imbalances of 66.09 kW, 37.02 kW, and 23.43 kW for DDPG, SAC, and TD3, respectively, while the power imbalance for the MDQN algorithm is 18.63 kW. The results indicate that the MDQN algorithm proposed in this paper outperforms other DRL algorithms during the training process. However, it is important to note that the tested DRL algorithms (including the MDQN algorithm) cannot strictly enforce power balance. Therefore, using these algorithms in real-time operations may lead to infeasible operations. To overcome this issue, this paper proposes a solution during online execution. 5.3 Online Execution
After training, the DNN parameters of all DRL algorithms are fixed, and performance comparisons are made on the test set. To compare the results on the test set, Figure 6 shows the cumulative operational costs and power imbalance of the four algorithms over a continuous period of 10 days.
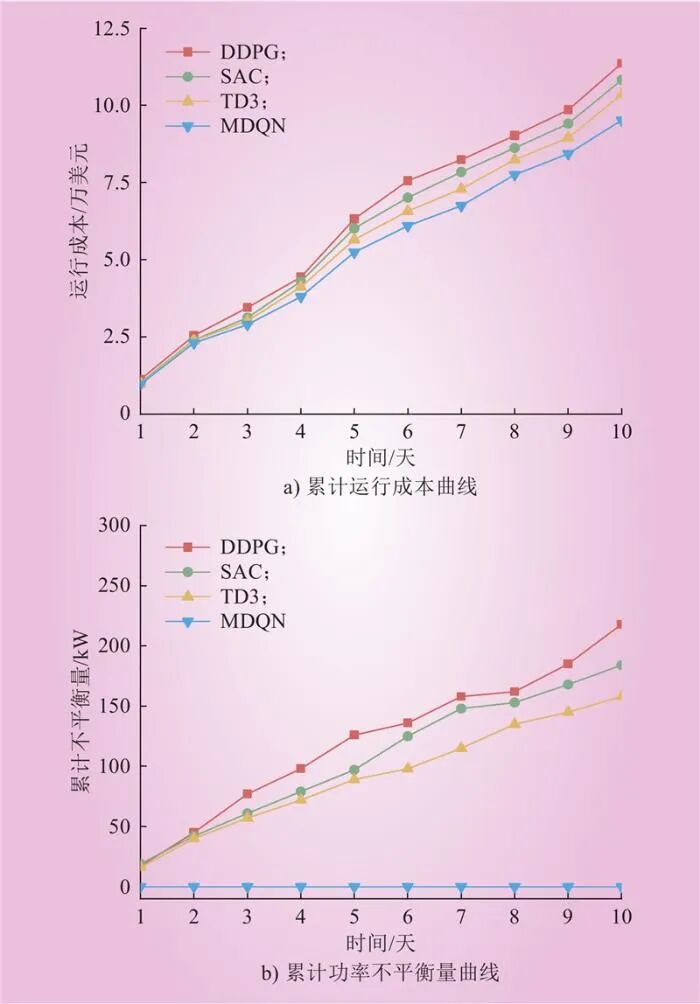
Figure 6 Cumulative 10-day Operating Costs and Imbalance of DDPG, SAC, TD3, and MDQNFig.6 Cumulative 10-day Operating Costs and Imbalance of DDPG, SAC, TD3, and MDQN From Figure 6, it can be seen that at the end of the test, the cumulative power imbalances for the DDPG, SAC, and TD3 algorithms are 218 kW, 184 kW, and 158 kW, respectively. However, the MDQN algorithm can strictly meet the power balance constraints, with operational costs of $113,600, $108,200, and $103,500 for the DDPG, SAC, and TD3 algorithms, respectively, while the operational cost for the MDQN algorithm is $95,200, which is 16.2% lower than that of the DDPG algorithm. This indicates that the MDQN algorithm performs better than other DRL algorithms in addressing power balance issues.
To verify the effectiveness of the algorithm in online decision-making, optimization is performed with an hourly time interval, and typical daily state data is used to test the performance of the algorithm. Figure 7 a) shows the information of load, photovoltaic, and electricity prices over 24 hours, while Figure 7 b) displays the operational results, including the charging and discharging power of all micro gas turbines and energy storage systems, as well as the power input/output from the grid. Additionally, Figure 7 c) shows the SOC (state of charge) of the energy storage system.
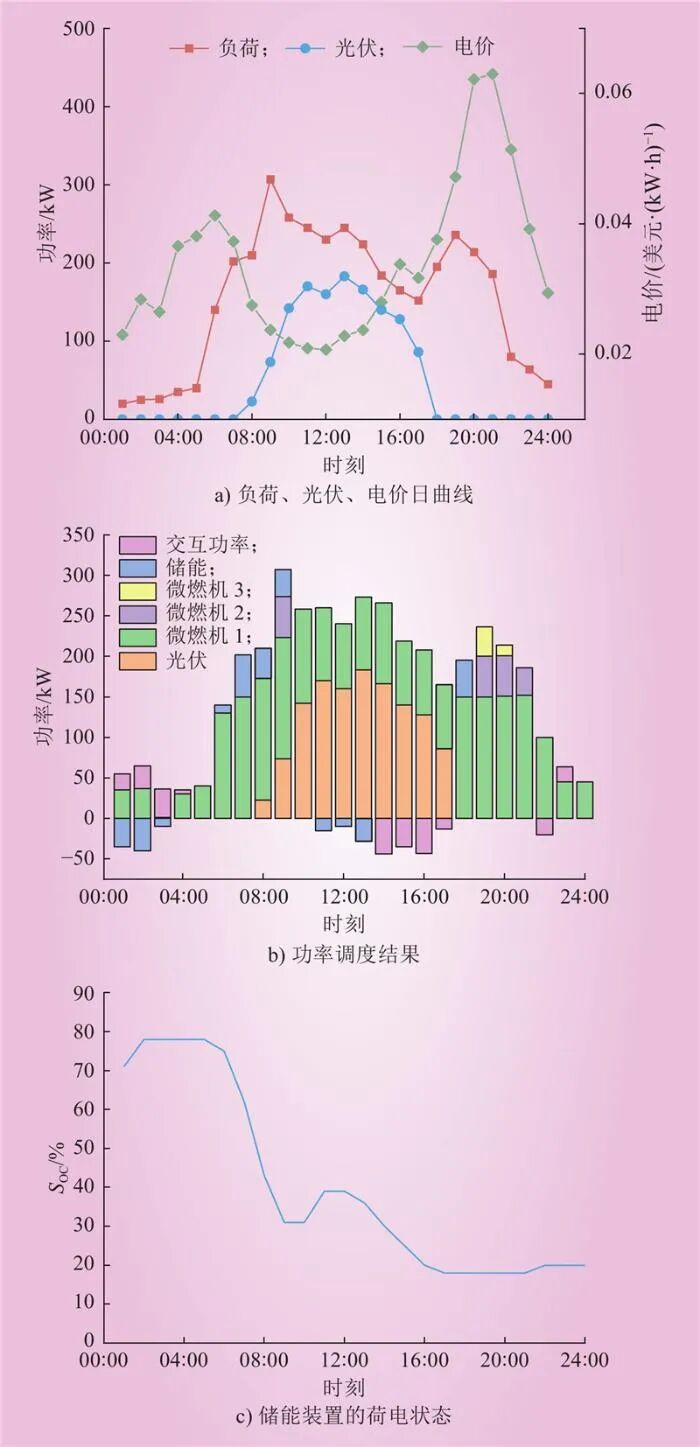
Figure 7 MDQN Optimized Operation Plans for All UnitsFig.7 MDQN Optimized Operation Plans for All Units From Figure 7, it can be observed that during the low electricity price non-peak hours (00:00—04:00), the energy storage system begins charging, reaching approximately 80% SOC; during peak hours (07:00—10:00, 17:00—21:00), the energy storage system is scheduled to discharge, and micro gas turbines are dispatched to fill the power gap. Notably, due to the lower operational cost of micro gas turbine 1, it is prioritized for use. When electricity prices are high, the micro gas turbines increase their output to meet load demands at the lowest operational cost. The above results indicate that the virtual power plant can flexibly manage dispatchable power sources to respond to changes in the external environment. By optimizing scheduling strategies, the VPP can achieve economic efficiency and manage energy resources effectively in real-time decision-making.5.4 Sensitivity Analysis
To analyze the impact of the hyperparameter σ2 in the reward function on the MDQN algorithm, different values of σ2 (20, 60, and 100) were used during training, and the changes in operational costs and power imbalance were observed, as shown in Figure 8.
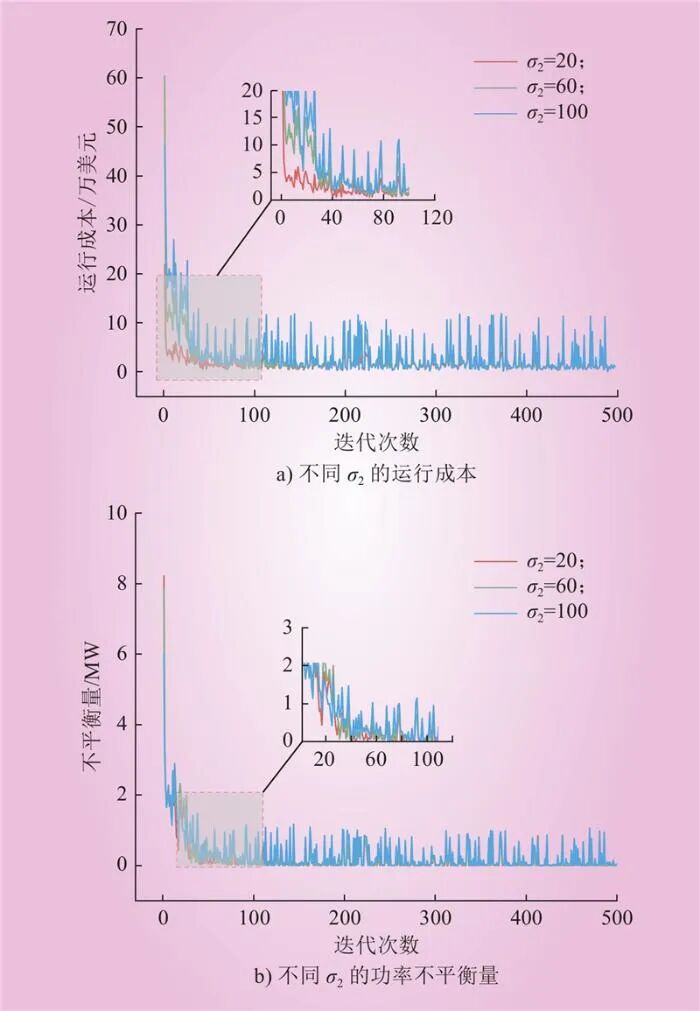
Figure 8 MDQN Operating Costs and Imbalance with Different σ2 ValuesFig.8 MDQN Operating Costs and Imbalance with Different σ2 Values From Figure 8, it can be observed that a higher
These results indicate that the selection of hyperparameter
06
Conclusion
This paper proposes an MDQN algorithm based on DQN and derives the following conclusions through case testing. 1) Simulation results verify that the MDQN algorithm has better training efficiency compared to DDPG, SAC, and TD3 algorithms, achieving higher cumulative rewards. It learns optimal strategies by exploring continuous action spaces within a more stable update rule. 2) The MDQN algorithm can strictly adhere to all operational constraints in the action space, ensuring that the scheduling plan formulated is feasible during real-time operation. This enables the VPP to effectively schedule and manage in practical operations. 3) By adjusting the hyperparameter σ2, the MDQN algorithm can focus more on reducing power imbalance or optimizing operational costs to meet different application needs. This provides a certain degree of flexibility for the optimization and adjustment of the VPP, allowing the algorithm to adapt to different scenarios and requirements.
Deep learning algorithms applied in virtual power plants avoid complex modeling processes while better addressing system complexity and uncertainty. However, they also come with some limitations and challenges: data acquisition and processing require substantial resources and time; complex algorithms demand significant computational resources and high-performance hardware; and the virtual power plant involves sensitive energy data and device control, necessitating attention to security and privacy issues.
Note: The content of this article has been slightly adjusted; please refer to the original text if needed.
Previous Issues Review
◀ Preview of “China Electric Power” 2024, Issue 1◀ Improved Byzantine Fault Tolerance Algorithm Consensus Mechanism for Multi-Virtual Power Plant Trading | “China Electric Power”◀ Research and Application of Control Strategy Optimization for Petal-shaped Distribution Network Area Backup System | “China Electric Power”◀ Collaborative Optimization Strategy for Virtual Power Plants Participating in Energy and Ancillary Services Markets | “China Electric Power”◀ Full-process Carbon Footprint Traceability of Dalian City Based on STIRPAT Model | “China Electric Power”◀ Call for Papers for the Column “Integration of Large-scale New Energy Vehicles and Urban and Rural Power Grids”◀ Call for Papers for the Special Topic “Modeling and Operational Decision-making of Distributed Flexible Resources for Smart Low-carbon Development”◀ Call for Papers for the Special Topic “Key Technologies for Protection and Control of New Distribution Systems”◀ Call for Papers for the Special Topic “Key Technologies for Safety of Lithium-ion Batteries for Energy Storage”Editor: Yu JingruProofreader: Wang WenshiReviewed by：Jiang DongfangStatementAccording to the latest regulations from the National Copyright Administration, when reprinting or excerpting works from the editorial department of “China Electric Power” in paper media, websites, Weibo, WeChat public accounts, etc., it is necessary to include the name of this WeChat account, QR code, and other key information, and to indicate “Original from China Electric Power” at the beginning. Individuals may forward and share according to this WeChat original text.Everyone is welcome to reprint and share.