🔸 Paper Information
Title:Joint Optimization Strategies for Multi-Service Communication and Computing Resources in 6G MEC
Authors::Wang Desheng, Deng Ke, Huang Zhihua, Zhang Hao, Lin Haohan
First Author Affiliation:School of Electronic Information and Communications, Huazhong University of Science and Technology
Abstract:The system latency and energy consumption of edge computing technology (MEC) are taken as the core indicators for joint optimization. A systematic mixed-integer nonlinear programming (MINLP) mathematical model is established for multi-cell and multi-terminal scenarios. By utilizing the idea of nested sparrow search algorithm in genetic algorithms, a joint optimization method from global to local is developed. Through analyzing the substitution mechanism between communication resources and computing resources, efficient terminal access selection, task offloading strategies, and optimization methods for transmission power and computing frequency are provided. This work serves as a positive theoretical guide for optimizing future new services in terms of timeliness and energy consumption, and offers beneficial exploration for the integrated design of communication, computing, storage, and control (4C) in future 6G systems.
Keywords:6G; Mobile Edge Computing; Communication-Computing Integration; Resource Allocation; Genetic Algorithm; Sparrow Algorithm
Citation Format:
Wang Desheng, Deng Ke, Huang Zhihua et al. Joint Optimization Strategies for Multi-Service Communication and Computing Resources in 6G MEC[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2023, 51(03): 1-6.
As the deployment of 5G accelerates, 6G has gradually become one of the key directions for international standard organizations such as ITU and 3GPP to collaborate, as well as a focal point for technological competition among countries. The U.S. government has established the Next G Alliance to seize the initiative in 6G and future mobile communications. In November 2019, China formed the IMT-2030 (6G) technology research and development promotion working group around the grand blueprint for 6G, conducting comprehensive exploration of demand, technology, and network architecture. China Mobile and others have released white papers summarizing the connection characteristics of 6G as typical scenarios of ubiquitous massive connections, expanding traditional communication resources to broader network resources, and utilizing computing network technology to coordinate the deployment of 4C (communication, computing, caching, control) resources in higher dimensions.
MEC can meet the user-side computing offloading needs, dynamically sharing resources from multiple base stations across domains, improving resource utilization and interference management capabilities, and adapting to the high computing and low latency characteristics of future network services. It is foreseeable that in the future, key nodes in the network and base stations will generally possess capabilities for content computing and storage. Under this background, the MEC architecture will play a significant role in the macro deployment and micro scheduling of resources in 6G.
The allocation of wireless carrying and computing resources for multiple terminals in MEC is generally achieved by adjusting the offloading decisions of terminals and optimizing the system’s resource deployment. The offloading decision problem related to computing services can be represented as a 0-1 integer programming problem, while parameters related to resource allocation, such as computing resources and channel bandwidth, are abstracted as continuous variables. Therefore, the optimization problem of edge computing is often represented as a mixed-integer nonlinear programming (MINLP) problem, which can be optimized using methods such as constraint transformation, condition relaxation, convex optimization theory, and branch-and-bound, but has high time complexity. As a result, most literature adopts heuristic algorithms to solve this problem to reduce time complexity. For example, Li et al. used a genetic algorithm (GA)-based joint optimization method to solve the user task completion time minimization problem under edge computing; Sun et al. applied the bat algorithm in vehicular network edge computing scenarios; Lyu et al. combined two methods, decomposing the original problem into two sub-problems: solving the resource allocation problem using convex optimization methods and optimizing the offloading decision using heuristic algorithms. In recent years, with the rapid development of machine learning, many researchers have also attempted to apply reinforcement learning to edge computing optimization algorithms. The trained models can meet certain specific environments and make rapid online decisions; however, reinforcement learning has poor generalization ability, weak dynamic adaptability, and the training cycle increases dramatically with the expansion of network scale, making it still immature at the application level.
In multi-cell edge computing scenarios, the single-service model is expanded to a multi-service model that is more aligned with practical application scenarios, while considering bandwidth and energy consumption constraints, using system latency and energy consumption as utility indicators to study the task offloading problem in edge computing. By decoupling the task offloading and resource allocation problems, the model is jointly optimized using genetic algorithms and sparrow algorithms.
1
System Model
The main service range of edge computing is for compute-intensive and latency-sensitive services, such as AR and VR. These types of services have high energy consumption and significant computing power requirements, thus offloading these tasks to edge servers for computation. The 0-1 offloading method treats the service as an indivisible whole, lacking flexibility; partial offloading divides the service into multiple sub-services, each of which can choose to be processed locally or offloaded to the edge server, which is more efficient but ignores the dependency relationships between sub-services in the actual system. Sub-services with dependency relationships are merged into a comprehensive sub-service, while sub-services without dependency relationships are still treated as independent sub-services.
1.1 MEC Modeling and Setup
The edge computing scenario is modeled as a multi-cell and multi-terminal scenario, where a single cell is a special case of multi-cell, as shown in Figure 1.
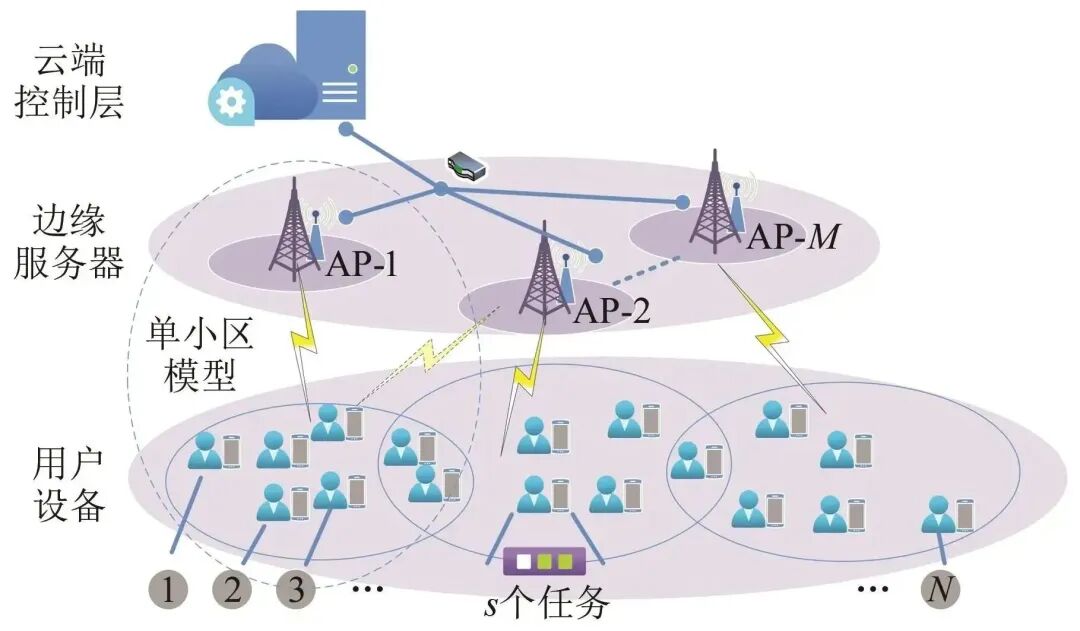
Figure 1 Business Scenario of Edge Computing
In this modeling scenario, the set χ represents N mobile user terminals χ={1,2,…,i,…,N}; the set Γ={1,2,…,k,…,M} represents M edge servers (access points); the number of services generated by terminal i in a unit time interval Ts is αi; the relevant parameters of the j-th service on terminal i are represented by the triplet {uij, cij, dij}, where uij represents the amount of input data required to execute the service, including control instructions for executing the service, service content, and running code, cij represents the number of CPU cycles required for the terminal or server to execute the service, and dij represents the amount of data for the computation result of the service.
Considering that sub-services are indivisible, each sub-service can only be processed either locally or on one of the servers, i.e., in the 0-1 offloading scenario, mij is used to represent the offloading method of the j-th service on terminal i. When mij=0, it indicates that the sub-service is executed locally; when mij=1, it indicates that the service is offloaded to the edge server for execution.
Each terminal can only connect to one access point (AP), using the variable ρik∈{0,1} to represent the access state of terminal i to base station k, where 1 indicates access and 0 indicates no access. A terminal can only connect to one AP, and cannot switch within a time slot, so the access method satisfies
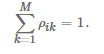
1.2 Communication Model
The communication method between mobile terminals and wireless access points (AP) adopts orthogonal frequency division multiple access. The number of terminals that an AP can accommodate does not exceed the total number of available sub-channels of the AP, ensuring that all terminals can connect to the corresponding AP and offload services to the MEC node via wireless means. The data transmission rate from terminal i to the wireless AP in the uplink is obtained using Shannon’s formula, specifically
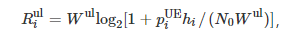
where Wul is the unit channel bandwidth of the uplink; piUE is the transmission power of terminal i; hi is the channel gain of the uplink between terminal i and the AP, determined by path loss; N0 is the power spectral density of noise in the channel between the terminal and the wireless AP. Similarly, the corresponding data transmission rate Ridl can be expressed in the form of equation (1) as
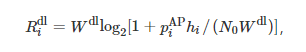
where Wdl is the unit channel bandwidth of the downlink; piAP is the downlink transmission power of the AP to terminal i.
1.3 Delay and Energy Consumption Analysis
1.3.1 Delay Analysis
The execution time of partially offloaded services should be determined by the maximum of the local execution time tiloc and the edge execution time tioff. The AP and edge server are connected by fiber, and the transmission delay is negligible compared to the wireless channel transmission delay, thus the time for offloading to the network edge is tioff=tiul+tiexe+tidl, which includes the user service upload time tiul, the edge server service computation execution time tiexe, and the time for the AP to return the computation result to the terminal tidl. According to the general rules of edge offloading computation, to improve processing efficiency, the edge server adopts parallel computation after receiving tasks from multiple different users.
a. Local Processing. Let the CPU frequency of terminal i be Filoc. If the j-th service of terminal i is executed locally, the execution delay tiloc is expressed as
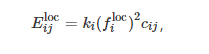
where mi=[mi1,mi2,…,mij,…,mis]; ci=[ci1,ci2,…,cij,…,cis]. Clearly, the delay for local execution is only related to the computing frequency of the user device.
b. Service Offloading. The time for terminal i to upload data to the AP can be expressed as
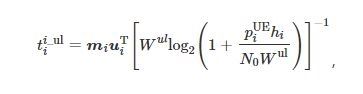
where ui=[ui1,ui2,…,uij,…,uis].
After the user service is uploaded to the AP, it must go through processes such as framing, and the upload time tiul after coordination is the maximum time of multiple different user services uploaded to the same AP, which can be expressed as
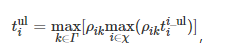
where the outer max function is used to select the AP to which the client terminal is connected; the inner max function is used to obtain the time of the user terminal that takes the longest to upload to that AP.
The edge server adopts a parallel computing method. The computation execution delay for each user is equivalent to the total computation delay of the target server to which the user offloads, i.e.,
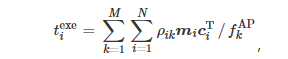
where fkAP is the computation frequency of the k-th edge server.
Subsequently, the AP returns the computation results to the terminal via the wireless downlink, and the downlink transmission time is expressed as
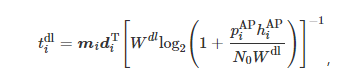
where di=[di1,di2,…,dij,…,dis].
Finally, the total delay for terminal i should be determined by the larger value of the local execution time tiloc and the edge execution time tioff, i.e., Ti=max{tiloc, tioff}.
1.3.2 Energy Consumption Analysis
There is a certain substitution relationship between energy consumption and processing delay consumption, which is also one of the important indicators that need to be comprehensively considered in the integration of communication and computing.
a. Local Processing. The energy consumed by executing services can be evaluated using dynamic voltage and frequency scaling (DVFS) technology, and the energy consumption calculation formula can be expressed as
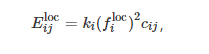
where ki is a constant related to the type of terminal chip; in this paper, the value is taken as 5.0×10-27. The energy consumption of terminal i’s service when executed locally is
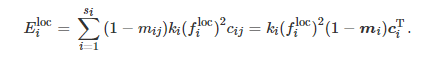
b. Service Offloading. The energy consumption process of offloading services to edge servers is analyzed by splitting it into three processes.
When terminal i uploads the service data to the AP, the energy consumption of the terminal is
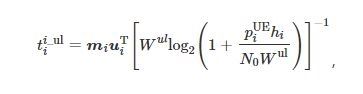
According to equation (2), the execution energy consumption of the edge server is
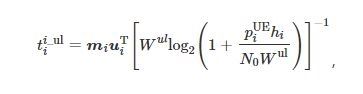
The AP returns the computation results to the mobile terminal via the downlink, and the downlink transmission energy consumption is
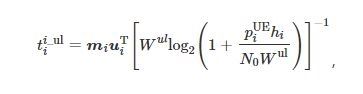
1.4 Model Problem Construction and Utility Function
By analyzing user delay and energy consumption, a systematic utility indicator for minimizing delay and energy consumption is established, constructing the model as a mixed-integer nonlinear programming (MINLP) problem. The average system delay and total system energy consumption are respectively:
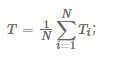
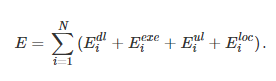
where delay is based on user experience, using the average delay perceived by the user as an indicator, and energy consumption is based on the system perspective, taking the sum of the energy consumption of the base station and the user as the utility indicator.
By introducing preference factors, the multi-objective optimization problem of delay and energy consumption is transformed into a single-objective optimization problem, defining the utility function of the edge computing system as U=λT+(1−λ)E
where λ∈[0,1] represents the preference coefficient between delay and energy consumption in the utility function, used to adjust the bias of the utility function towards delay and energy consumption. The optimization objective of the model can be established as a minimization optimization problem

where equation (5) represents the constraint on the computation frequency of the edge server; equation (6) represents the transmission power constraint of the mobile terminal, where the rated transmission power of each terminal cannot exceed the maximum transmission power; equation (7) represents the mobile transmission power constraint of the edge server; equation (8) indicates that each service of the mobile terminal can only choose to be processed on the edge server or locally, which is a 0-1 integer constraint; equation (9) indicates that from the user’s perspective, individual delay must be less than the maximum deadline for the task; equation (10) indicates that each mobile user terminal can only connect to one AP.
2
Optimization Algorithm Design
2.1 Overall Architecture of Model Solving Algorithm
The multi-cell and multi-terminal computation offloading and resource allocation problem is modeled as a MINLP problem, optimizing task offloading strategies, base station computation frequency, mobile terminal transmission power, and terminal transmission power; the task offloading strategy is a discrete variable, while transmission power and CPU computation frequency are continuous variables. A dual-layer optimization model using a genetic algorithm nested with a sparrow algorithm is adopted. For the input data {uij, cij, dij}, the genetic algorithm first randomly initializes the population, where the individuals in the population are feasible solutions for the offloading strategy, and then performs genetic operations to obtain the next generation population. The sparrow algorithm optimizes the resource scheduling strategy for each individual in the next generation population and obtains the fitness value of the individual. This generation of the population undergoes genetic operations to obtain a new generation of the population, and the above steps are repeated until the iteration ends. The model architecture diagram is shown in Figure 2.
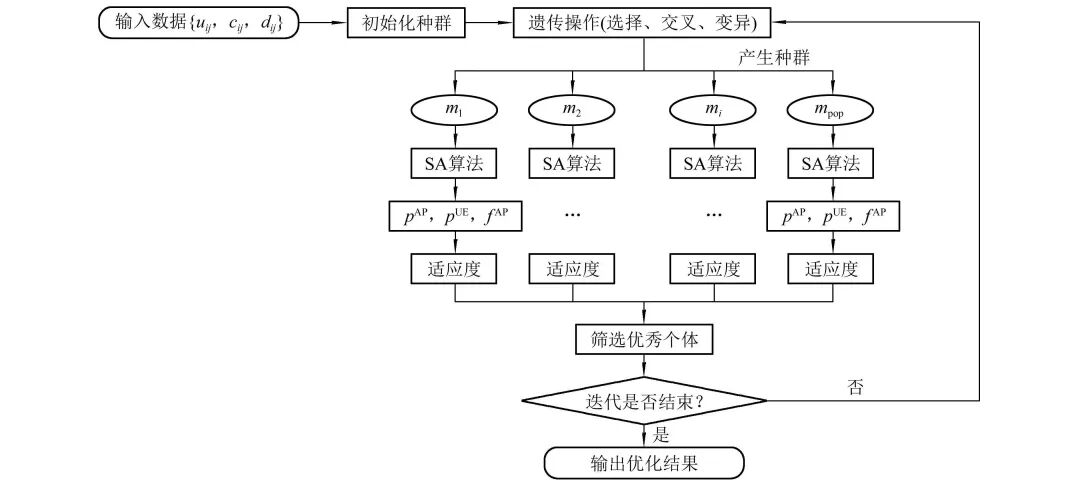
Figure 2 Dual-Layer Optimization Model of Genetic Algorithm Nested with Sparrow Algorithm
The dual-layer optimization model allows the genetic algorithm and the sparrow algorithm to perform their respective roles, optimizing discrete variables and continuous variables, and narrowing the search space of both algorithms through a stepwise nested approach, accelerating the algorithm’s solution.
2.2 Fitness Function Design
Furthermore, to balance the delay fairness among users and the load balancing of base station offloading, a delay penalty term and a balance penalty term are added to the objective function U in equation (3) as the fitness function during the optimization process, i.e.,
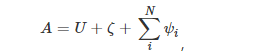
where the penalty term ψi is the delay penalty term, corresponding to the constraint (9) of the objective function, which is difficult to achieve through partitioning the solution space, thus designed as a penalty term. The design of this constraint is to avoid user experience degradation due to saturation of the edge server load. The penalty term formula is expressed as
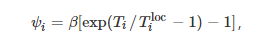
where β is the penalty coefficient, which can adjust the punishment intensity. When the execution time Ti of the mobile terminal is greater than the local execution time Tiloc, this penalty term will cause the fitness to increase, leading to a degradation of the solution; while when Ti is less than Tiloc, this penalty term will provide a slight reward to the fitness.
The penalty term ζ is the load balancing penalty term. In practical scenarios, users tend to connect to the base station with the best channel conditions or the nearest one, which can cause the function to fall into local optima, leading to low system energy efficiency. Based on the prior knowledge that load balancing of base stations can better utilize edge computing resources, a load balancing penalty term ζ is added to optimize the algorithm’s solution,
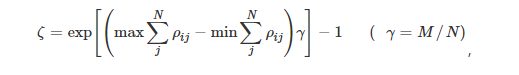
where the exponent part of exp represents the difference between the maximum and minimum load of the edge servers. Uneven load among edge servers will lead to an increase in fitness; the more balanced the load, the smaller the penalty term. γ is the balancing coefficient, used to adjust the magnitude of the penalty term, and experimental results show that using the number of base stations M divided by the number of users N yields good results.
2.3 GA-SSA Algorithm
For the discrete variables such as task offloading strategy m and access strategy ρ, they can be encoded into two different chromosome sequences for input into the GA. The current task offloading strategy of the mobile terminal is encoded as a chromosome sequence using {0,1} encoding, referred to as the offloading decision chain, specifically
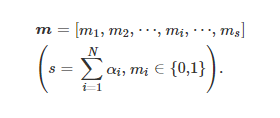
The access strategy for the terminal is encoded in integer form as a chromosome sequence, referred to as the access strategy chain, specifically
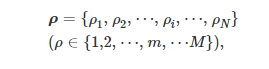
where ρi=m indicates that the client terminal i connects to edge server m.
The offloading decision chain and access strategy chain do not interfere with each other during crossover. To enhance the convergence speed and accuracy of the genetic algorithm, an adaptive method is used to adjust the crossover rate and mutation rate. For parent chromosomes with better fitness, the mutation rate and crossover rate are smaller to preserve excellent genes; while for parent chromosomes with poorer fitness, the mutation rate and crossover rate are larger to explore excellent genomes.
After the genetic algorithm generates the populations of offloading strategy m and access strategy ρ, the sparrow algorithm search is performed on the chromosome sequences to obtain the optimal continuous variables, including terminal transmission power pUE, AP transmission power PAP, and the computation frequency f allocated by the AP.
3
Simulation and Result Analysis
Simulations are conducted on the Matlab platform, with the operating system being Ubuntu 20.04. The important parameters and values for the simulation are shown in Table 1.
Table 1 Simulation Environment Parameter Settings
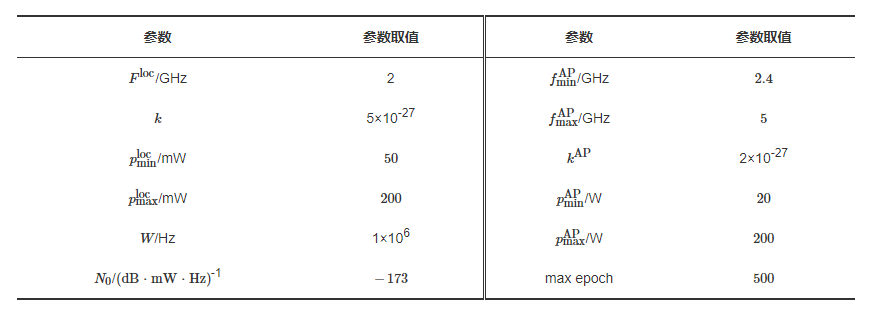
Figure 3 shows the convergence graph of the algorithm iterations for multiple cells, with the number of users N being 60, the number of tasks s being 5, and the number of edge servers M being 4. It can be seen that convergence begins around 200 generations, but the fitness value continues to decrease and converge, which is consistent with expectations.
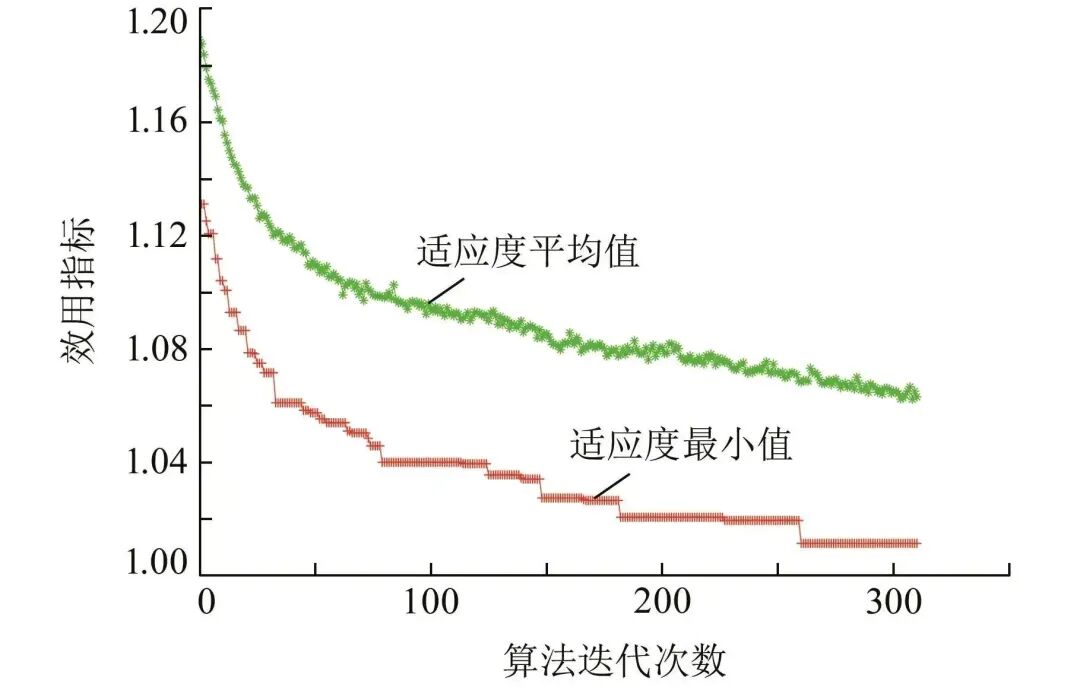
Figure 3 Convergence of Multi-Cell Algorithm Model
Figure 4 presents the performance of different offloading strategies under different numbers of tasks and users. The proposed optimization algorithm is compared with three strategies: full local computation, full offloading computation, and random offloading computation. In terms of performance indicators, the algorithm in this paper significantly outperforms the other three offloading strategies. Based on this preference coefficient, the system energy consumption and average system delay are also better than other strategies, which aligns with the expected outcomes of the algorithm.

Figure 4 Comparison of Various Offloading Strategies
Figure 5 illustrates the relationship between energy consumption and delay optimization of the model under different preference coefficients λ, with the number of users N being 60, the number of tasks s being 5, and the number of edge servers M being 4. As the delay preference coefficient increases, the system optimization shifts from favoring energy consumption to favoring delay, which is consistent with the theoretical model analysis. In the specific system design process, considering the diversity of services, the preference coefficient can be adjusted according to the actual needs of the system for energy consumption and delay, based on the computational load and delay sensitivity of different services, to achieve performance trade-off optimization and improve user service QoE experience.
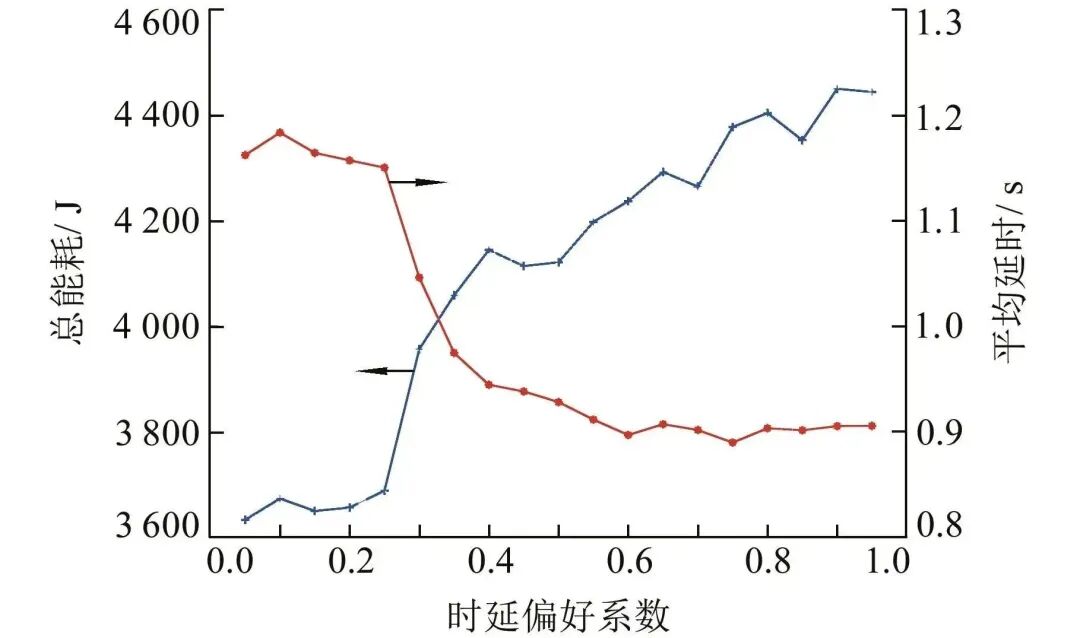
Figure 5 Situation of Various Offloading Strategies with Different Numbers of Users
It can be seen that the proposed GA-SSA dual-layer optimization model, which nests the sparrow algorithm within the genetic algorithm, effectively narrows the search space of both algorithms through a stepwise nested approach, accelerates the algorithm’s solution, and demonstrates good performance in terms of system delay, energy consumption, and fitness indicators. Furthermore, it analyzes the performance trade-off curves when the preference coefficients of delay and energy consumption parameters in the objective function change, providing guidance for selecting weight coefficients for different application scenarios and different business QoE. Simulations indicate that the time consumption for single-sample solving in the GA-SSA algorithm can reduce the convex optimization time scale from hours to minutes. The next step will utilize this model to generate a large number of samples for statistical learning, combining resource offloading with deep learning models, and exploring new directions for high-dimensional resource pre-deployment and implementation scheduling based on AI computing power.
Click to view this issue’s column ▼

2023 Issue 3
6G: Communication, Sensing, and Intelligent Integration
END

