Formal Methods Based on SCADE Models

In the previous issue of the embedded systems special, we provided a detailed overview of the birth, development, and application of Ansys SCADE (See: Embedded Systems | A Retrospective on Ansys SCADE). This article will focus on “Formal Methods Based on SCADE Models”. To put it simply, formal methods abstract a program into a mathematical formula and then use rigorous mathematical reasoning to prove or disprove that formula. Given the many testing methods available in the current software industry, why do we still need formal methods?

As Edsger Wybe Dijkstra, the Turing Award winner of 1972, said: “Program testing can be used to show the presence of bugs, but never to show their absence!” This means that testing can only indicate the presence of errors in a program but cannot indicate that there are no errors. Unless the tests conducted on the program can exhaust all possible scenarios, traditional testing methods cannot guarantee the safety and reliability of the system completely. It can be said that only formal methods can fundamentally ensure the safety and reliability of the system, which is particularly important in safety-critical systems.

In the 1960s, Hoare Logic was the first doctrine about formal methods. For a long time since then, formal methods were mainly applied in academia and gradually expanded into the industrial application of hardware. Objectively speaking, formal methods have seen more successful applications in the world of electronic hardware—mainly because hardware tools are more standardized and stable, whereas the software field has not yet reached that level. In software system design, models corresponding to high-level requirements may lack sufficient detail to allow meaningful analysis of certain properties, resulting in generally poor application effects and practical value of formal methods. Currently, formal methods are more applicable at the detailed design level (Low-level requirement), particularly for models of software behavior.

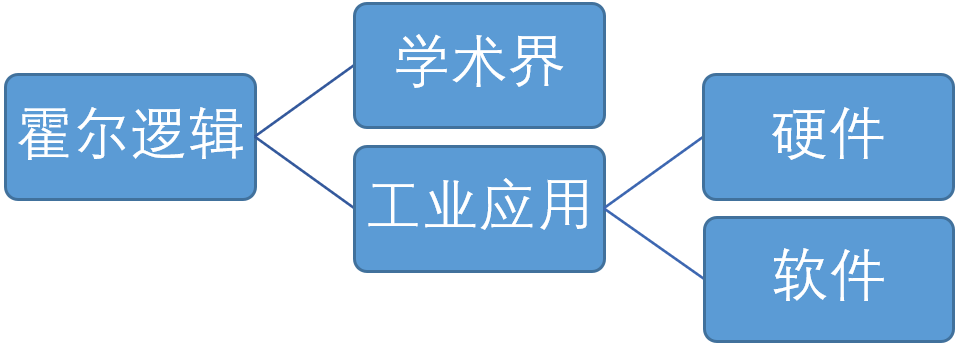
The Development and Application of Formal Methods

The supplementary document to the airworthiness standard for airborne software, DO-178C, titled “DO-333, Supplement on Formal Methods for DO-178C and DO-278A” (hereinafter referred to as “DO-333”), defines formal methods as: a descriptive symbolic system and analytical method used to construct, develop, and reason about a system’s behavior through a mathematical model. In short, formal methods = formal models + formal analysis. The most important advantage of using formal methods for verification is its completeness, as it can mathematically and logically prove the correctness of the system design. However, the disadvantages of formal methods are also noteworthy; they require repeated refinement, abstraction, extraction, and refinement of the original design to ultimately obtain its mathematical model. This process demands a high level of mathematical skills, project understanding, and engineering experience from the user.

A formal model is the foundation of formal methods; the model must have clear, mathematically defined syntax and semantics to qualify as a formal model. The applicability of formal methods to any specific software development activity is limited by the ability to construct appropriate formal models. Natural language and semi-formal languages may include properties that cannot be reasoned using formal methods, making it impossible to fully simulate software in many cases. Therefore, defining model limitations is necessary.

With these limitations in place, formal models can serve as a complete and accurate means of describing important software properties. Formal analysis can then provide guarantees for these properties and be combined with other verification techniques (e.g., testing) to achieve satisfactory fulfillment of all verification goals.

Formal methods can be used in many stages of the project development lifecycle and meet various verification objectives. Wherever formal models are used, they should be verified to ensure they accurately represent the software. This means that for the properties being analyzed, if they apply to the model, they should also apply to the actual software.

While creating formal models during the software development cycle has clear benefits, the greatest advantage of formal methods lies in the formal analysis conducted on these models. Formal analysis can provide guarantees or evidence that software properties and software meet requirements. Providing guarantees or evidence means that all possible execution scenarios are considered, i.e., completeness. To perform formal analysis, a set of software properties is necessary. These properties can be created or embedded in specific tools for formal analysis (e.g., worst-case execution time analysis). The properties of formal analysis can often be viewed as similar to verifiable testing requirements. In testing, test cases should be easily derived from verifiable requirements; for formal analysis, properties are often also the test cases to be verified. A complete set of properties can be defined for a set of requirements, in which case this set of properties serves as evidence proving the equivalence of the analyzed model to its requirements.

It is worth mentioning that formal analysis can only be termed as such when the deterministic analysis of the properties is robust and reliable. Robust analysis means that when a property may not be “true,” formal methods do not assert it as “true.” Conversely, asserting a property that may be “true” as “false” is acceptable. This is a matter of usability, not reliability. In simple terms, generating “false alarms” is permissible. Additionally, when attempting to prove whether properties hold, it is acceptable for the results of formal methods to return “unknown” or not return a conclusion. In such cases, additional verification (refining properties, adjusting analysis engines, etc.) is required.

Because formal methods = formal models + formal analysis, the vast majority of model-based development tools in the software industry cannot be said to employ formal methods unless they are specifically customized or converted, as the models themselves are not formalized. However, SCADE, due to its foundational language originating from formal languages like Lustre, SCADE is the only truly formal model among mainstream commercial tools, and combined with third-party formal analysis engines (Prover, S3, SafeProver, GATel, etc.), it has already achieved numerous successful cases of formal method verification across various industries.

The aforementioned “DO-333” document identifies three typical categories of formal analysis, defined as follows:

Abstract Interpretation (also known as Static Analysis): Defines a conservative representation of the semantics of a programming language, used for the reasonable determination of dynamic properties of finite state programs… It can be viewed as a partial execution of a computer program that determines specific effects of the program (e.g., control structures, information flow, stack size, number of clock cycles), without actually executing all computations.

The method of abstract interpretation is relatively simple and can use static analysis tools to check for issues such as division-by-zero, out-of-bound array access, overflows, etc., but may generate false warnings.

Relevant mainstream commercial tools include AbsInt’s Astree, Mathworks’ Polyspace Code Prover, and TrustInSoft’s TrustInSoft Analyzer.

Model Checking: Searches all behaviors of a formal model to determine whether a specified property is satisfied.

Model checking is used to determine whether the formal model of the system satisfies correctness properties based on specifications. Model checking typically has three outcomes: 1. Property holds; 2. Property fails, providing a counterexample; 3. Analysis times out (TO: Time Out) and cannot determine. Compared to abstract interpretation, model checking provides a better representation of safety properties. However, due to limitations in processing capabilities for nonlinear algorithms and state space explosion, its scope of use is also limited. For engineers, the greatest value of model checking lies in its ability to automatically generate counterexamples when safety properties are violated. When safety properties cannot be verified, it can show the execution trace that leads to the erroneous state.

Relevant mainstream commercial tools include Kind2 (University of Iowa), JKind (Rockwell Collins), CEA’s GATeL, and Prover Technologies’ Design Verifier.

Deductive Proof: Uses mathematical proofs to establish each property of a formal model. Typically, a theorem proving tool is used to construct proofs to show that software properties hold.

Deductive proof uses mathematical parameters to determine each property of a formal model, with the ultimate goal being theorem proving. The proofs are usually based on Hoare logic and Dijkstra’s precondition reasoning. Compared to abstract interpretation and model checking, deductive proof is more effective. However, this method typically requires very specialized personnel, has a lower degree of automation, and even ordinary reasoning verification can often take weeks or even months, making it difficult to apply in large-scale projects, and in some cases, it may even be impossible to use. Relevant mainstream tools include STeP (Stanford Theorem Prover), ACL2, HOL, PVS, TLV, Coq, etc.

All three types of formal analysis share some commonalities. First, they all rely on formal models. Non-formal models or composite models that mix non-formal and formal models are insufficient for formal methods to demonstrate compliance between specifications and code, so they must be true formal models. Second, all formal analyses are typically implemented using a tool.

The following diagram provides an overview of formal analysis, showing that the automation levels and the amount of code that can be handled by the three methods are arranged from high to low, while the completeness of safety property proofs is arranged from low to high.

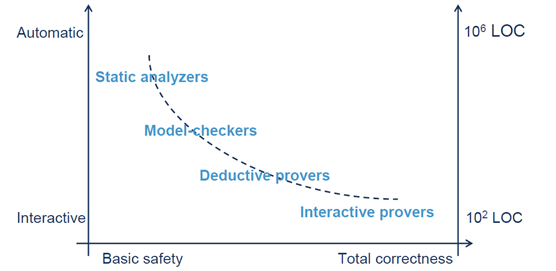
Overview of Formal Analysis, adapted from Xavier Leroy

Among the three types of formal methods, abstract interpretation and model checking are more widely applied in engineering practice. SCADE has already integrated formal analysis tools based on both abstract interpretation and model checking technologies (from companies like AbsInt and Prover). Abstract interpretation can generally yield standard analysis results quickly through simple button operations, which will not be further described here; however, obtaining results from model checking requires some effort, and some complex projects may require significant effort from engineers to apply successfully. The following section will provide an in-depth introduction to model checking.

Model checking, as a framework that encompasses a series of verification techniques for finite state systems, was first proposed by Clarke, Emerson, Queille, and Sifakis in 1981, and some of them received the Turing Award in 2007.

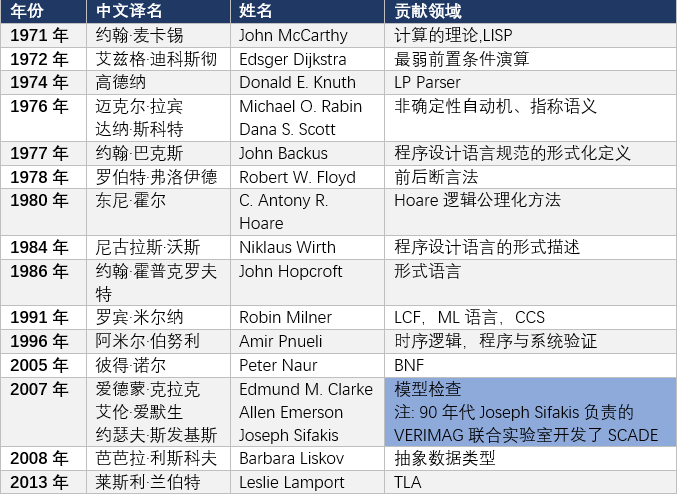
Some Turing Award winners’ research in formal verification

The model checking method primarily verifies whether a system meets certain key system properties by traversing the finite state space of the system. The inputs for model checking are typically two: a system described by an automata model and a set of system properties described by temporal logic formulas. The model implements the behavior of the system, while the properties describe what the system should or should not do.

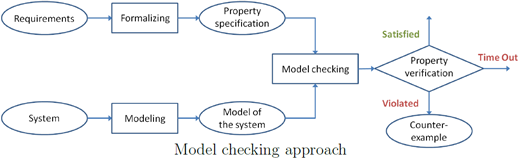
Methods of Model Checking

Both the system model and the properties to be verified need to be described in a highly abstract and precise manner. In recent years, the concept of hybrid systems has been used in academia to describe embedded systems in safety-critical fields, characterized by the inclusion of both continuous time behaviors (described using differential equations) and discrete logical control (described using state machines or automata), which are not independent of each other but are intertwined together, collectively forming the complex logic that describes real systems. As shown in the previous article “A Retrospective on Ansys SCADE”, SCADE has developed from real applications in the industry and is precisely a fusion product that includes various formal languages such as differential equations, state machines, and automata, capable of meeting the requirements of hybrid systems. Therefore, SCADE is one of the better tools for implementing system models in formal methods.

The property description language is typically expressed using temporal logic formulas. Temporal logic formulas are a mathematical form tailored for statements and reasoning involving time, closely resembling natural language, and they come with formal semantics. Common temporal logic formulas include Linear Temporal Logic (LTL) and Computation Tree Logic (CTL). The combination of LTL and CTL is referred to as CTL*.

To date, the algorithms for model checking have roughly developed through three generations.

The first generation is Explicit/State Model Checking, which explicitly explores the state space of the model and searches through forward exploration until a property conflict is found. This method proposes different approaches for LTL and CTL. In LTL model checking, exploration algorithms can be depth-first or breadth-first: the breadth-first method can find the shortest possible counterexample but has significantly higher memory usage requirements than the depth-first method. In CTL model checking, a recursive calculation of whether each state satisfies the sub-formulas is performed to determine the set of all states satisfying the given property. If all states are accessed and no violations are detected, the model is deemed to satisfy that property. Unsurprisingly, the first-generation model checking methods encountered the state space explosion problem.

The second generation is Symbolic Model Checking, which uses a special data structure called Binary Decision Diagrams (BDD) to represent sets of states and functional relationships more efficiently, allowing for the representation of larger state spaces.

The third generation is Bounded Model Checking (BMC), which is a supplementary method based on BDD for symbolic model checking. The BMC technique has been proposed and widely applied by scholars. Its main idea is to limit the number of behavioral steps of the model through an integer k, encoding the system’s behavior within k steps into a set of Boolean constraints, and then solving them based on SAT (Boolean Satisfiability) methods to efficiently identify all errors within k steps. Although the BMC method is limited in that it can only verify properties within a threshold, it surpasses traditional model checking methods in its ability to discover errors. Additionally, since the BMC method only needs to traverse the state space of the model within the threshold, it enhances the scale of systems it can handle, which is one of the widely recognized advantages of BMC.

Unlike semi-automated or fully manual theorem proving, model checking can be executed automatically and provides corresponding error information when the system does not satisfy properties. Therefore, it is more favored in the industry compared to other formal methods. However, due to the high complexity of model checking technology, it remains challenging to handle large-scale systems in the industry. A report released by Rockwell Collins indicates that model checking technology can conduct meaningful analyses for finite cases with non-linear properties and reachable state spaces smaller than 10200.

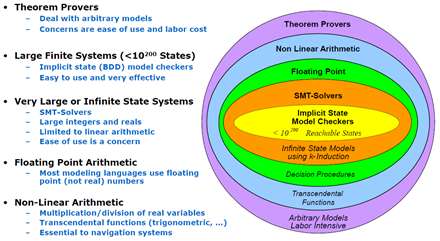
Domain of Scalable Verification by Steven P. Miller on Model Checking Technology

The majority of commercial tools for formal analysis of SCADE models adopt model checking technology based on the BMC method. Currently, SCADE in the 2020 R1 version includes the Design Verifier engine from Prover Technology, which has an embedded SAT solver that can perform model checking on SCADE models, automatically providing counterexample test cases when the results indicate an error.

The general method for achieving formal verification using SCADE models is: maintain the original design model unchanged, define an observation model containing safety properties based on requirements, and then design a top-level operator to connect the design model and the property observation model, ultimately analyzing the output of the property model.

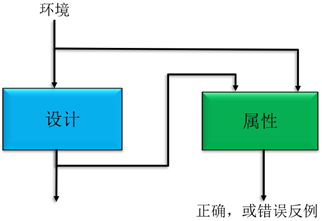
SCADE Model Checking Method Diagram

The detailed workflow for formal methods based on SCADE models is as follows.

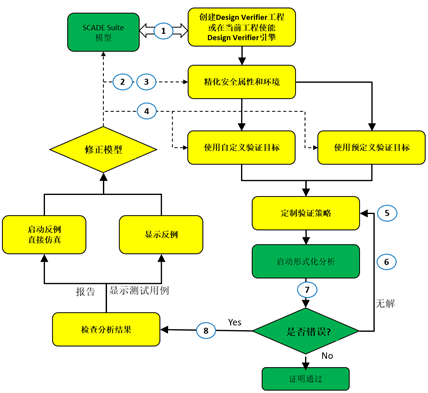
Workflow for Formal Methods of SCADE Models

1. Create a new formal verification project or enable the formal analysis engine in the current development project, which will automatically import the predefined Suite library related to formal verification into the project.

2. Define the observer model based on safety requirements and usage scenarios, where the safety properties included are also designed using the Suite, and the output of these properties must be designed as a boolean type, with a true value indicating safety for the formal engine to analyze.

3. Create a top-level operator that connects the original design model and the observer/property model. The Assert function can be used in the top-level operator to add constraints and exclude irrelevant scenarios to accelerate the formal analysis process.

4. Create custom formal verification targets based on safety properties or directly enable the built-in predefined formal verification targets in the Suite.

5. Customize the formal verification strategy and apply it to the formal verification targets.

6. Start the formal engine for analysis.

7. Output the results of the formal verification.

8. Check the results; if true, it is verified; if false, import the given counterexample for model simulation, and based on the simulation results, revise the model and iterate for the next round of formal analysis.

The four built-in predefined formal verification targets mentioned in step 4 are:

• Division-by-Zero Check: Division-by-Zero PO: Verify if there is a possibility of division by zero.

• Overflow Check: Overflow PO: Verify whether numerical data types overflow during assignment, shifting, or type conversion, etc.

• Dynamic Access Check: Dynamic Access PO: Verify whether array indices are out of bounds, etc.

• Consistency Check: Consistency PO: Verify whether assumptions and constraints are consistent, constraints can be added by the Assume function.

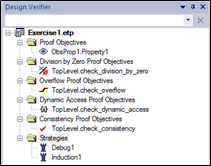
SCADE Formal Verification Panel

In step 5, the formal verification strategies mentioned include the following three:

SCADE Formal Verification Strategies

The attributes and meanings of the properties in the Debug and Induction strategies are as follows:

Attributes of SCADE Strategies

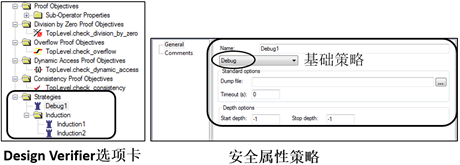
SCADE Design Verifier Tab and Safety Property Strategies

Using formal verification strategies helps users:

• Quickly find bugs early in the development process.

• Prove that a requirement is correct by verifying the safety properties corresponding to an independent complete requirement.

• Save verification costs and improve product credibility.

The design of the top-level operator for formal analysis of a certain project is shown in the chart.

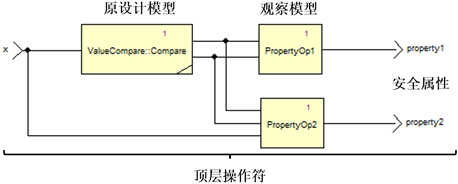
Design of a Certain Top-Level Operator in SCADE

The correct and incorrect output results of formal analysis are shown in the following diagram.

SCADE Formal Analysis Correct or Incorrect Results

When formal analysis indicates an error, you can click the hyperlink on the detailed error interface to jump to the safety property. You can also, under the condition of correct configuration, directly click Load Scenario to import the test cases provided by the counterexample for white-box simulation.

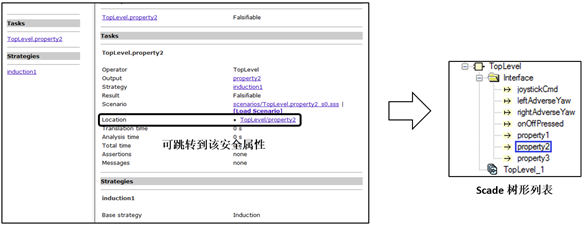
SCADE Formal Analysis Error Importing Counterexamples for White-Box Simulation

Finally, you can check each analysis result in HTML format in the SCADE program or in the project directory.

SCADE Formal Analysis Directory-Level Web Format Report

Model checking is conventionally used to determine whether the formal model of a system satisfies correctness properties based on specifications. This is the conventional use of model checking. Interestingly, many scholars have proposed that model checking technology can also be used to generate test cases related to coverage analysis. This method requires reverse design, deliberately designing a set of “trap properties” that claim: a certain branch can never be covered no matter how it runs. If model checking proves that this “trap property” is false, a counterexample can be obtained, and that counterexample serves as a test case that can cover that branch. Mathematically, this involves performing non-emptiness detection on the automata described above, and the result should be non-empty.

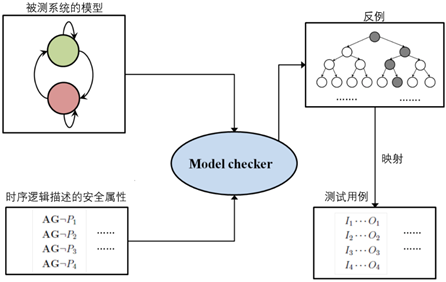
Model Checking Generates Test Cases

Similar to the positive use of model checking methods, checking the “trap properties” will also encounter the state space explosion problem. Under the premise that the system model is already determined, how to design appropriate “trap properties” in the shortest possible time is key to improving the efficiency of test case generation. Subsequent articles will introduce the applications of formal methods in projects using SCADE tools across various industries.

This article introduces formal methods based on SCADE models in conjunction with the supplementary document “DO-333, Supplement on Formal Methods for DO-178C and DO-278A” of the airworthiness standard for airborne software, DO-178C. Formal methods = formal models + formal analysis. Formal methods are mainly divided into three categories: abstract interpretation, model checking, and deductive proof. SCADE is the only truly formal model among mainstream commercial tools, which can be combined with various third-party formal analysis engines to implement formal methods. SCADE has integrated formal analysis tools based on both abstract interpretation and model checking technologies (from companies such as AbsInt and Prover).

It is worth mentioning that Ansys and Honeywell have collaborated for many years in the field of embedded systems, and in the future, they will jointly develop and optimize the in-house formal verification toolchain Hi-Lite for aviation projects, gradually making it a standard module of SCADE.

[1] Leanna Rierson. Safety-Critical Software Development and Certification—DO-178C Standard Practice Guide[M]. (Cui Xiaofeng). Beijing: Electronic Industry Press, June 2015.

[2] Todorov V, Boulanger F, Taha S. Formal Verification of Automotive Embedded Software[C]//Proceedings of the 6th Conference on Formal Methods in Software Engineering. ACM, 2018: 84-87.

[3] Xavier Leroy Trust in Compilers, Code Generators, and Software Verification Tools [EB/OL].

[4] Song Jun. LTLNFBA: Conversion from LTL Formulas to Büchi Automata[D]. Xi’an University of Electronic Science and Technology, 2014.

[5] Wang Rui. Research on SAT-based Symbolic Model Checking Technology[D]. National University of Defense Technology, 2014.

[6] Sun Y. Strengthening Functional Validation of Critical Systems by Using Model Checking: Application to Instrumentation and Control Systems in Nuclear Power Plants[D]. 2017.

[7] Li W, Kan S, Huang Z. A Better Translation from LTL to Transition-Based Generalized Büchi Automata[J]. IEEE Access, 2017, 5: 27081-27090.

[8] Liu Zhifeng. Research on Key Technologies in Model Checking and Its Applications[D]. Nanjing University, 2011.

[9] Xie Dingbao. Research on Bounded Model Checking Optimization Technology for Hybrid Systems[D]. Nanjing University, 2016.

[10] Miller S P. Bridging the Gap Between Model-Based Development and Model Checking[C]//International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Springer, Berlin, Heidelberg, 2009: 443-453.

[11] SCSDV_2019R1_M01_Tool. Ansys SCADE Suite Design Verifier and Formal Verification [EB/OL]. Ansys SBU. 2019 (Internal Document)

https://xavierleroy.org/talks/ERTS2018.pdf. Embedded Real-Time Software and Systems, 2018-02-02

[12] Bhatt D, Madl G, Oglesby D, et al. Towards Scalable Verification of Commercial Avionics Software[M]//AIAA Infotech@ Aerospace 2010. 2010: 3452.

[13] Wang J, Zhan NJ, Feng XY, Liu ZM. Overview of Formal Methods. Journal of Software, 2019, 30(1): 33-61 (in Chinese). http://www.jos.org.cn/1000-9825/5652.htm

[14] Introduction to Formal Methods[M]. Tsinghua University Press, Zhang Guangquan, 2015.