Follow SomedayWill, providing assistance to those tormented by computer organization.

Yesterday’s P2 haunt still lingers, indeed it was somewhat challenging. Someday did not finish debugging the Challenge, which is a bit regrettable. However, thanks to the inspiration from WJJ, Someday found the first two problems quite easy. Today, I will summarize these clever tricks learned along with my own discoveries, hoping that those who did not pass P2 will not lose heart and keep trying.
(My sister is really strong)
The most clever trick: do-while loop
We will use the example of matrix multiplication in MIPS from the P2 assignment to explain why the do-while loop is the most clever and how to write it in the best way.
Assuming we have three matrices A[n][n], B[n][n], C[n][n], where C = A * B, then:
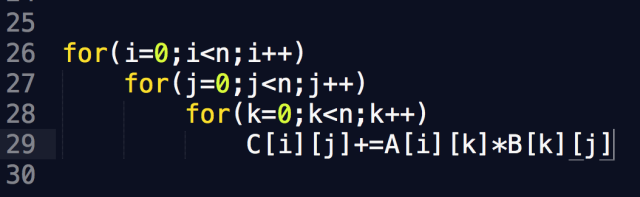
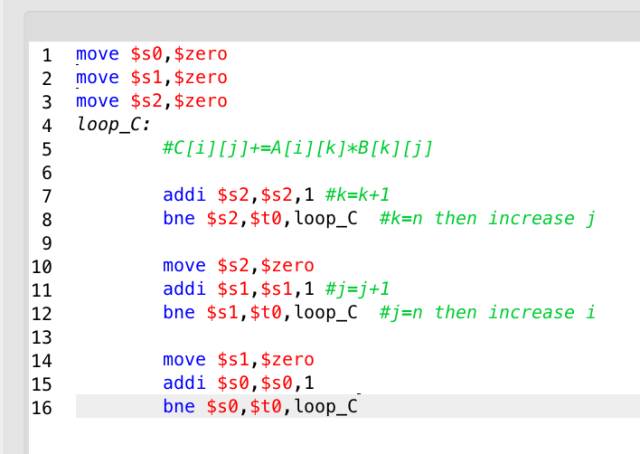
This is very simple to write in C, but if we write a for loop in MIPS, it will look like this:

It can be said to be very ugly, because one for loop requires two labels and two jumps.
If we remove the matrix multiplication part, we can see that the framework looks like this, which is the most straightforward three nested for loops, requiring six labels and six jumps.
However, the P2 tutorial provided a writing method that, upon careful consideration, seems incredibly clever. Someday initially went straight to solving the problems without looking at the tutorial and only realized it while chatting with WJJ. Thus, I organized the content as follows.
This story tells us to engage in discussions with experts.
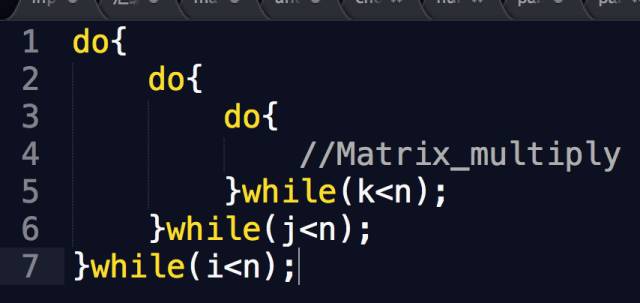
Here is another way to write matrix multiplication:

This version includes empty lines and comments, and after removing the intermediate calculations, it becomes even more concise.
Subjectively, the amount of code is reduced by about half, and objectively, this three-level do-while loop only requires one label and three jumps!
Let’s dig deeper; there are three questions that need clarification:
Question 1: Why is this a do-while?
Question 2: Why is one label and three jumps sufficient?
Question 3: What are the limitations of this method?
Question 1: Why is this a do-while?
It is evident that we update the loop variable i and perform jump operations only at the end of the loop, so this is a do-while loop.
Question 2: Why is one label and three jumps sufficient?
This is the most critical point. Let’s look at the structure of the do-while in matrix multiplication:
We can observe that since there is nothing between the three do statements, these three do statements essentially equate to one do, as each loop starts from the Matrix_multiply point.
In C, you can only write three do statements, but in assembly language, you can accomplish it with one label!
Question 3: What are the limitations of this method?
Theoretically, there is no difference in what do-while and for can accomplish.
However, if there are some boundary conditions, such as the first power of the matrix in this P2 being itself, this boundary condition may be the reason many people did not pass P2.
This type of boundary condition may require special handling before the do-while loop.
Additionally, if there are operations between the three do statements, then can we still use one label? Not necessarily; operations can be placed after the three while statements, but this makes it more complex and does not highlight the advantages of this method.
To summarize, in assembly language, when there are multiple nested loops and no operations between the loop statements (as in matrix multiplication), using this do-while writing method is incredibly satisfying.
The best part is that this method is very suitable for copy-pasting. Someday quickly passed the second question using this method, taking 60 minutes to complete the first two questions, although I still ended up with a wrong answer on the third question QAQ.
Inspired by this, are there any other similar clever tricks?
Of course, there are, such as multiple nested if statements.
In C, if you need to implement multiple if statements, you can sometimes use logical expressions directly:
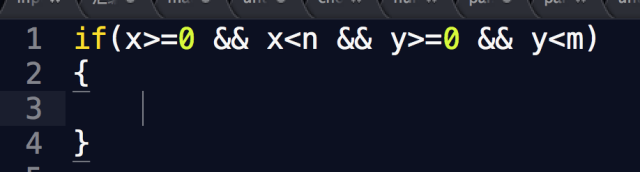
One if does the job.
In MIPS, you can also use logical operations, but many may not be accustomed to it. If you change it to four nested if statements, it would require eight labels, which is quite ugly:
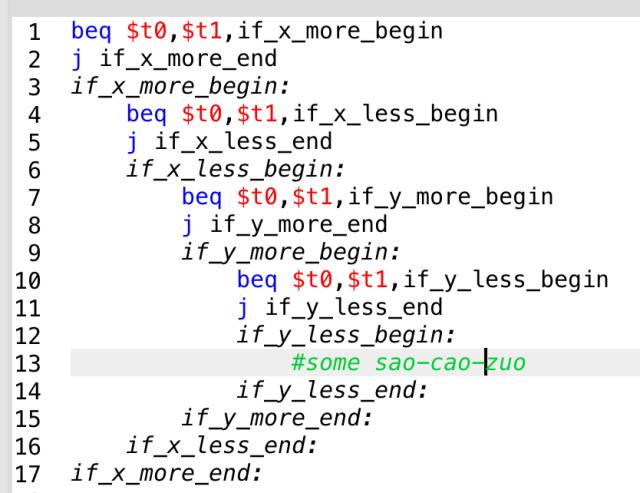
(Registers are written arbitrarily)
But in reality, if one of the conjunctions fails, we can exit early, so we can use one ending label:
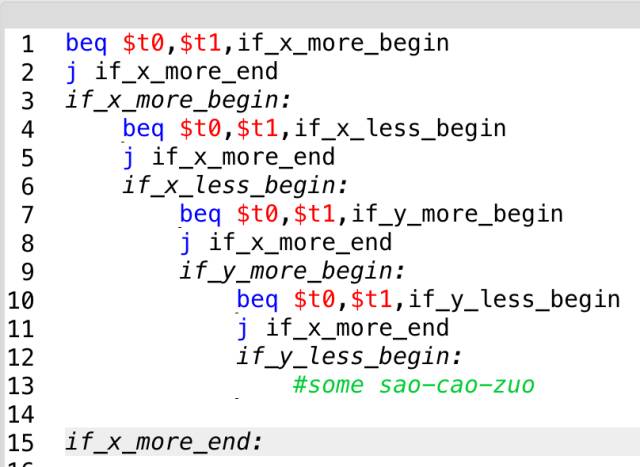
This also achieves a good simplification.

Once again, thanks to WJJ for answering Someday’s questions.
Once again, I hope those who did not pass P2 will not lose heart and keep trying.
Once again, I hope experts will contribute clever tricks for computer organization; as long as they are clever enough, you can earn a knee from Someday, and your genius tricks will also be shared with those tormented by computer organization through Someday’s posts.

(Someday thinks of themselves as cute)
SomedayWill
Growth, waiting, hope
Reward
