This content is sourced from the Journal of Geodesy, 2022, Issue 8 (Review No. GS Beijing (2022) 0490)
Zhang Baocheng1 , Ke Cheng1,2, Zha Jiuping1, Hou Pengyu1,2, Liu Teng1, Yuan Yunbin1, Li Zishen3
, Ke Cheng1,2, Zha Jiuping1, Hou Pengyu1,2, Liu Teng1, Yuan Yunbin1, Li Zishen3
1. State Key Laboratory of Geodesy and Earth Dynamics, Institute of Precision Measurement Science and Technology Innovation, Chinese Academy of Sciences, Wuhan 430071, Hubei; 2. School of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049; 3. Institute of Aerospace Information Innovation, Chinese Academy of Sciences, Beijing 100094
Funding Projects: National Natural Science Foundation (42022025; 41774042); Hubei Province Key Research and Development Program (2020BHB014)
Abstract: Emerging industries such as intelligent driving, precision agriculture, and drones require Global Navigation Satellite System (GNSS) to provide faster and more accurate navigation and positioning services. Undifferenced and uncombined PPP-RTK integrates the advantages of Precise Point Positioning (PPP) and Real-Time Kinematic (RTK), allowing for flexible processing of multi-frequency and multi-mode data to achieve rapid high-precision positioning with wide regional coverage. However, PPP-RTK is still in the technical research and development stage, and its industrial application has not yet fully formed. This paper constructs the undifferenced and uncombined PPP-RTK model based on code division multiple access (CDMA) and frequency division multiple access (FDMA) from theory to practice, develops corresponding real-time computation software, and creates a prototype terminal. Based on the precise correction products estimated from the Beijing-Tianjin-Hebei reference network with an average station spacing of 154 km, the prototype terminal was mounted on drones, agricultural machinery, and cars to conduct real-time dynamic positioning tests. The test results show that the ambiguity fixing times for the PPP-RTK prototype terminal in three scenarios were 5, 2, and 7 seconds, respectively, with ambiguity fixing success rates of 99.79%, 99.14%, and 98.96%, and horizontal and vertical positioning accuracies of about 1 cm and 4 cm, respectively. The test results prove that the self-developed PPP-RTK prototype terminal can provide continuous, reliable, and high-precision positioning services.
Keywords: Global Navigation Satellite System Undifferenced And Uncombined Real-Time PPP-RTK Prototype Terminal


ZHANG Baocheng, KE Cheng, ZHA Jiuping, et al. Undifferenced and uncombined PPP-RTK: algorithmic models, prototype terminals and field-test results[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(8): 1725-1735. DOI: 10.11947/j.AGCS.2022.20210465 
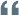
The Global Navigation Satellite System (GNSS) has been widely applied in national defense construction, transportation, and precision agriculture, while the rapid development of these fields has also raised higher requirements for GNSS precision positioning technology[1–5]. Traditional Precise Point Positioning (PPP) suffers from slow convergence, making it difficult to obtain high-precision positioning results quickly[6–7]. Real-Time Kinematic (RTK) achieves fast convergence but relies on a dense reference network[8–9]. To overcome the limitations of these two traditional precise positioning technologies, a faster and more flexible PPP-RTK technology has emerged[10].
PPP-RTK technology integrates the advantages of both PPP and RTK technologies, broadcasting state correction parameters to users according to the PPP service model and then utilizing RTK technology’s ambiguity fixing strategy to achieve rapid high-precision positioning from a single measurement station[10–11]. Scholars at home and abroad have proposed various PPP-RTK methods, mainly including UPD/FCB[12], integer recovery clock[13], decoupled clock[14], and undifferenced and uncombined common clock methods[15]. The first three methods are based on ionosphere-corrected combined observations, while the undifferenced and uncombined common clock method starts directly from raw observations, which is beneficial for processing current multi-frequency and multi-mode data[16–17]. Notably, the undifferenced and uncombined method retains all original parameters, and applying constraints considering the physical characteristics of the parameters can enhance model strength, while the simultaneously estimated correction parameters are fully consistent and globally optimal[18–20]. Additionally, the author’s team has recently expanded undifferenced and uncombined PPP-RTK from systems using code division multiple access (CDMA) signals to systems using frequency division multiple access (FDMA) signals, thus constructing a unified and complete multi-frequency and multi-mode undifferenced and uncombined PPP-RTK theoretical algorithm[21].
As the PPP-RTK theory matures, several institutions at home and abroad have established software experimental platforms to promote the application of PPP-RTK technology. For example, the French National Center for Space Studies (CNES) has developed PPP-Wizardd[22], the Canadian Geodetic Survey has developed CSRS-PPP[23], Wuhan University has developed PRIDE-PPPAR[24], and the Shanghai Astronomical Observatory has developed the Net_Diff software. These software currently focus on scientific research and have not yet been ported to user terminals to provide services for the public and industry. Embedding research-oriented post-processing software into terminal devices for real-time operation requires complex code upgrades and integration. The code running on terminal devices must be compatible with their operating systems, consider their limited computing and memory resources, and organically integrate and allocate their built-in communication interfaces, thus requiring the code to be concise, efficient, highly cohesive, and loosely coupled.
This paper constructs CDMA and FDMA undifferenced and uncombined PPP-RTK server and user models from theory to practice, develops corresponding industrial application software, and simultaneously develops an integrated PPP-RTK prototype terminal based on the ARM Cortex-A8 chip and the HeXingXing UM4B0 high-precision GNSS module. Using the precise correction products estimated from the Beijing-Tianjin-Hebei reference network with an average station spacing of 154 km, the terminal was mounted on drones, agricultural machinery, and urban cars to conduct a series of real-time positioning tests, demonstrating the service performance of undifferenced and uncombined PPP-RTK in practical application scenarios.
1 Undifferenced And Uncombined PPP-RTK Model
This section constructs the undifferenced and uncombined PPP-RTK server and user models, including the model based on pseudorange and phase observations under CDMA signal system and the model that uses only phase observations under FDMA signal system.
1.1 CDMA PPP-RTK Model
In a regional reference network, assume that receiver r (r=1, 2, …, n) tracks signals transmitted by satellites s (s=1, 2, …, m) at frequency j (j=1, 2, …, f), while considering the spatial correlation of regional ionospheric delay, establishing the following full-rank model for the PPP-RTK server[21]
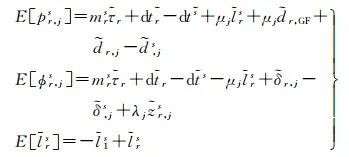 (1)
(1)
Where E[·] is the expectation operator; pr, js and ϕr, js represent the pseudorange and phase observations containing all precise corrections, respectively. In the server data processing, the reference station coordinates are precisely determined in advance, thus the satellite-to-ground distance is also included in these pseudorange and phase observations. lrs is the ionospheric virtual observation of the single difference between stations, set to 0[25], and its uncertainty is described by a random model. This paper adopts the random model proposed in reference [26], which considers the spatial correlation of ionospheric delay based on the distance between stations and the satellite elevation angle. The symbols on the right side marked with a tilde refer to estimable parameters rather than original parameters, with specific explanations and definitions provided in Table 1, where each estimable parameter is a linear combination of its original parameters and other parameters. Among them,
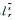 (2)
(2)
Table 1 Estimable Parameters and Their Definitions of CDMA PPP-RTKTab. 1 Estimable parameters and their definitions of CDMA PPP-RTK
| Estimable Parameters | Symbols and Definitions |
| Tropospheric Delay | 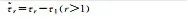 |
| Receiver Clock Bias | 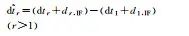 |
| Satellite Clock Bias |  |
| Ionospheric Delay | 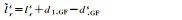 |
| Receiver Pseudorange Bias | 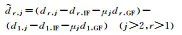 |
| Receiver Differential Pseudorange Bias | 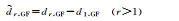 |
| Satellite Pseudorange Bias | 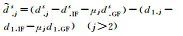 |
| Receiver Phase Bias | 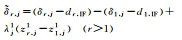 |
| Satellite Phase Bias | 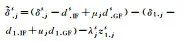 |
| Ambiguity | 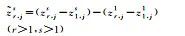 |
The two types of combinations of ionospheric delay and geometric non-related satellite pseudorange biases (d, IFs and d, GFs) and other parameters in this paper follow equation (2).
The server estimates the satellite clock bias, satellite pseudorange and phase biases, as well as tropospheric and ionospheric correction products, which are transmitted to the user measurement station u, establishing the following user-side positioning model[21]
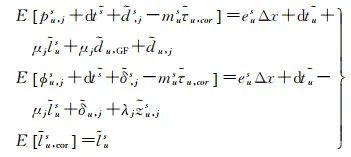 (3)
(3)
In this equation, the left side represents the tropospheric correction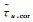 based on the tropospheric delay estimated by the server,
based on the tropospheric delay estimated by the server,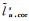 is modeled based on the ionospheric thin layer model (with a thin layer height set at 350 km) to obtain the estimated slant ionospheric delay from the server. The right side Δx is the user position vector, with coefficients eus being the line-of-sight vector from the receiver to the satellite; other parameters are defined similarly to those on the server side.
is modeled based on the ionospheric thin layer model (with a thin layer height set at 350 km) to obtain the estimated slant ionospheric delay from the server. The right side Δx is the user position vector, with coefficients eus being the line-of-sight vector from the receiver to the satellite; other parameters are defined similarly to those on the server side.
This paper directly models the slant ionospheric delay rather than the vertical ionospheric delay. If the vertical ionospheric delay were to be modeled, a mapping function would need to be selected to convert the slant ionospheric delay to vertical ionospheric delay. However, due to the precision of the ionospheric mapping function, converting to vertical ionospheric delay would result in a loss of accuracy, ultimately affecting positioning accuracy. Directly modeling the slant ionospheric delay avoids this problem.
1.2 FDMA PPP-RTK Model
Unlike CDMA signals, GLONASS uses FDMA signals, where the wavelengths of different GLONASS satellites observed at the same time differ (denoted as λjs), resulting in frequency inter-bias (IFB). To avoid the impact of pseudorange IFB, this paper adopts the latest proposed FDMA PPP-RTK server model that utilizes only phase observations
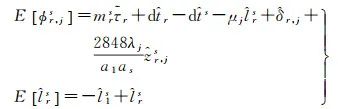 (4)
(4)
In this equation, the tropospheric delay has the same estimable form as the CDMA model, while the estimable forms of other parameters have changed. Specific definitions are provided in Table 2. It is especially noteworthy that the estimable form of ambiguity is no longer in the standard double-difference form but rather a specific linear combination of ambiguity, and its coefficients have also changed. Here, λj is the wavelength corresponding to the center frequency of GLONASS; as=2848+κs; κs∈ [−7, +6] is the channel number of GLONASS satellites.
Table 2 Estimable Parameters and Their Definitions of FDMA PPP-RTKTab. 2 Estimable parameters and their definitions of FDMA PPP-RTK
| Estimable Parameters | Symbols and Definitions |
| Tropospheric Delay | 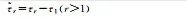 |
| Receiver Clock Bias | 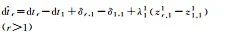 |
| Satellite Clock Bias | 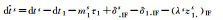 |
| Ionospheric Delay | 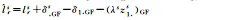 |
| Receiver Phase Bias | 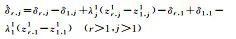 |
| Ambiguity | 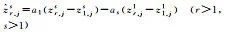 |
Although the ambiguity in equation (4) has integer characteristics and is estimable, its equivalent wavelength is approximately 0.1 mm, and fixing it as an integer does not guarantee the integer characteristics of the original ambiguity. Therefore, further conversion of the estimable ambiguity in equation (4) to integer estimable ambiguity is required to achieve tight ambiguity fixing; specifically, the estimable ambiguity and its coefficients in equation (4) need to be replaced with integer estimable ambiguity and its coefficients, as detailed in reference [27]. Due to its complex analytical form, iterative computation is required, and this paper will not elaborate further.
To intuitively display the GLONASS integer estimable model and analyze its ambiguity fixing performance, the author takes the example of observing 7 GLONASS satellites at a certain epoch, constructing the coefficient matrix of the integer estimable ambiguity for frequency j as λjL
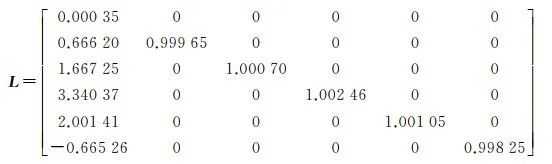 (5)
(5)
Observing its diagonal elements, only the first element is very small, while the others are close to 1. This indicates that only the first ambiguity of each frequency has a very small equivalent wavelength, making it difficult to fix, while the other ambiguities are not the same. To ensure the correct fixing of GLONASS ambiguity, a partial ambiguity fixing strategy is adopted, where at most m−2 (m is the number of satellites) ambiguities can be fixed for each frequency, rather than m−1 ambiguities.
Since GLONASS only broadcasts dual-frequency FDMA observation values, equation (4) does not consider observations of three frequencies or more. The phase biases of the first two frequencies of the satellites are selected as references and are not estimable. Therefore, only correcting the satellite clock bias, ionospheric, and tropospheric delays is sufficient to construct the user-side model[21].
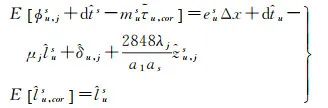 (6)
(6)
Similarly, the estimable ambiguity needs to be converted to integer estimable ambiguity to achieve tight ambiguity fixing.
2 Undifferenced And Uncombined PPP-RTK Software Platform
Based on the above undifferenced and uncombined PPP-RTK model, the author’s team has developed a post-processing/real-time multi-frequency multi-GNSS PPP-RTK software platform—NASDAK (network augmented satellite data analysis kits)[28]. NASDAK is written in standard C language and mainly includes two parts: server and user, supporting GPS/BDS/Galileo/GLONASS multi-frequency data processing. The server can run stably for a long time on both Windows/Linux systems, while the user side supports operation on Windows and embedded systems.
Figure 1 shows the software structure and data processing flow of NASDAK, including 4 subprograms on the server side and 1 user-side subprogram. The server data reception/decoding/distribution subprogram (NASDAK-SVR) acquires reference network observation data, broadcast ephemeris, and precise satellite product binary real-time streams from the public network/dedicated line. According to the corresponding protocol standards, it decodes the binary messages into decimal data, and then broadcasts the decimal structure to the local area network via broadcast protocol. The product computation and modeling main program (NASDAK-NET) obtains data and products from the local area network broadcast port, performs network parameter estimation, and obtains satellite clock biases, satellite pseudorange and phase biases, as well as ionospheric and tropospheric delay products. After modeling the ionospheric and tropospheric delays, all products are sent to the encoding broadcasting subprogram. The product encoding broadcasting subprogram (NASDAK-Encode) receives product structure data packets from the main program at a specific port, encodes various products according to specified standards, and sends them to the user management subprogram for authorized relaying or to the satellite control center for injection into satellite broadcasts to the ground. Finally, the user positioning program (NASDAK-USR) obtains precise correction values from the network or satellite to perform precise point positioning with fixed ambiguity at a single station. Additionally, the data monitoring subprogram (NASDAK-MON) serves as a mirror program for the PPP-RTK product computation main program, replacing the main program’s parameter estimation with data quality statistical analysis, and replacing the main program’s product output with data backup and statistical information output. This module is independent, and its statistical information is not received by other modules, only for post-analysis.
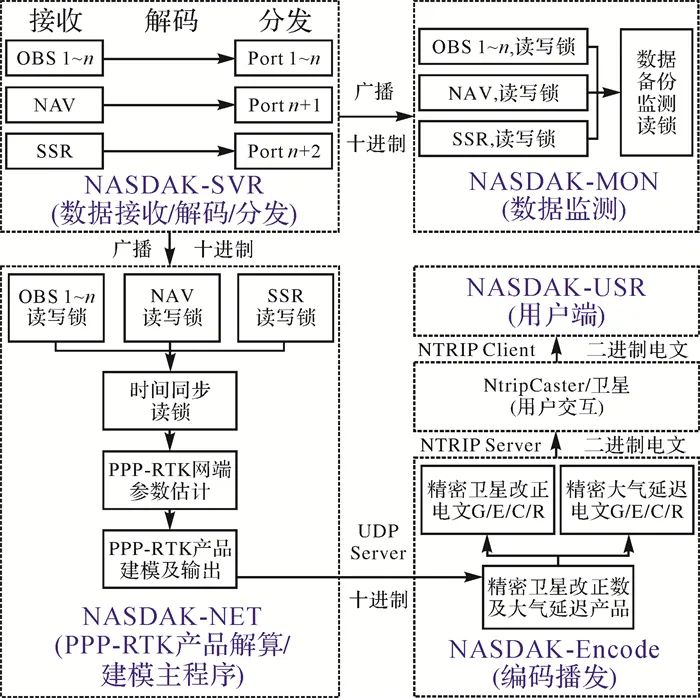 |
| Figure 1 PPP-RTK Software Structure and Data Processing Flow[28]Fig. 1 Structure and working flow of the PPP-RTK software[28] |
|
Figure Options |
3 Undifferenced And Uncombined PPP-RTK Prototype Terminal
3.1 Hardware Design
Targeting high-precision navigation and positioning users, the PPP-RTK prototype terminal uses the HeXingXing UM4B0 high-precision full-system and full-frequency GNSS module. As shown in Figure 2, the PPP-RTK prototype terminal consists of three main parts: communication module, sensor module, and core computing module. The communication module includes the ESP8266 Wi-Fi module, which can receive external precise correction information via network communication mode using the Ntrip protocol, and can also communicate via satellite using TCP/IP protocol. The GNSS module is the HeXingXing UM4B0 high-precision GNSS module for the full system and full frequency. Both the Wi-Fi module and the GNSS module are connected to the core board via serial ports. An external DB25 interface connects to the RS232 interface for real-time output of results in serial mode. Additionally, the core board’s rich ROM resources and external TF card interface can ensure that positioning results and software logs are stored in file form for post-analysis.
 |
| Figure 2 PPP-RTK Core-Board and Prototype TerminalFig. 2 PPP-RTK core-board and prototype terminal |
|
Figure Options |
3.2 Software Foundation
The PPP-RTK prototype terminal is based on the ARM Cortex-A8 chip and the OK335 core board, which has rich ROM/RAM resources and can run the Ubuntu operating system. The core board communicates with the Wi-Fi module and GNSS module via serial ports. On one hand, it connects to the server via the Wi-Fi module and sends a GET request carrying user authentication and mount point information for real-time access to the server’s Ntrip protocol real-time precise correction products in transparent mode; on the other hand, it configures the UM4B0 GNSS module via commands to obtain raw observation data from the full-frequency and full-system GNSS. After completing all necessary real-time stream data reception and decoding, the terminal can perform single-station PPP-RTK user-side computation and output NMEA/custom format positioning results in real-time via serial ports. At the same time, it saves the positioning results, log files, and quality control files in file read/write mode for post-analysis.
4 Experiments And Results
To evaluate the positioning performance of the undifferenced and uncombined PPP-RTK prototype terminal, this paper conducted three major application scenarios using the PPP-RTK server products calculated from the Beijing-Tianjin-Hebei reference network. These scenarios include: unmanned system applications mounted on drones, smart agriculture applications mounted on agricultural machinery, and intelligent driving applications mounted on cars. This section first introduces the reference network data and processing strategies, then evaluates the positioning performance of the PPP-RTK prototype terminal in the three scenarios.
4.1 Experimental Data And Processing Methods
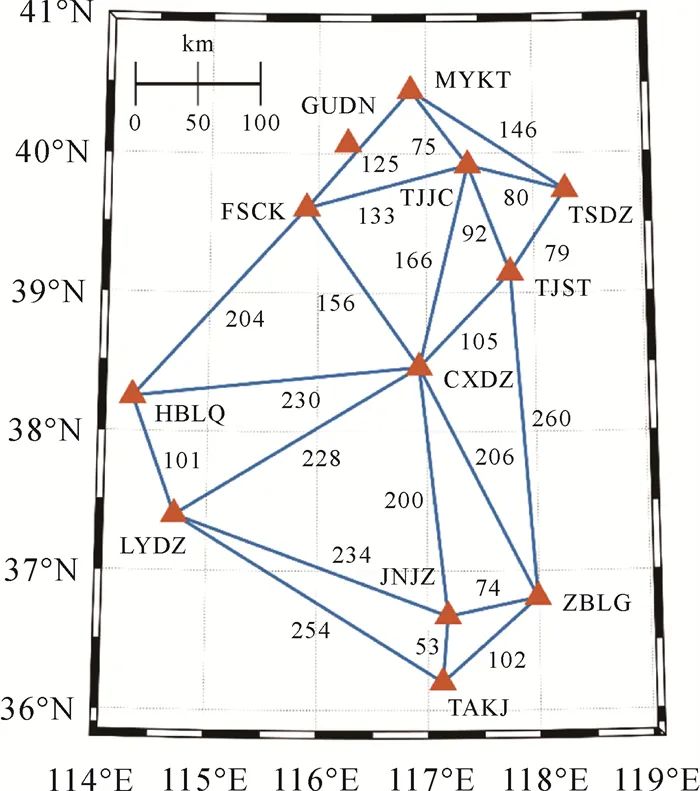
The distribution of the Beijing-Tianjin-Hebei reference network is shown in Figure 3, where the 11 reference stations connected by solid blue lines cover parts of Beijing, Tianjin, Hebei, and northwest Shandong, with an average station spacing of 154 km. Each reference station is equipped with a HeXing UR4B0-D receiver and HXCCGX601A HXCS antenna, tracking GPS (G) L1/L2, BDS2/3 (C2/3) B1I/B3I, and GLONASS L1/L2 data, with a data sampling rate of 1 Hz.
 |
| Figure 3 Distribution of the Beijing-Tianjin-Hebei Reference NetworkFig. 3 Distribution of the Beijing-Tianjin-Hebei reference network |
|
Figure Options |
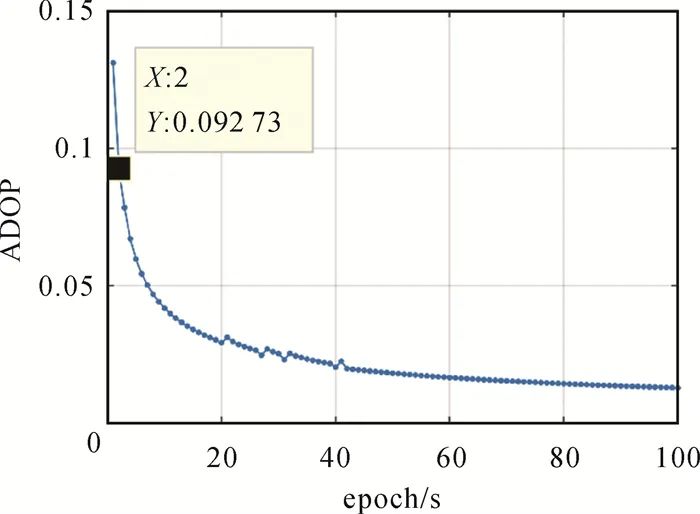
The GUDN station does not participate in server product computation and will be used as a reference station for short baseline RTK, with RTK solutions serving as reference values for comparison with PPP-RTK results. The drone and vehicle tests were conducted near the GUDN station, while the agricultural machinery test was carried out near the MYKT station. In the three scenarios of drone, agricultural machinery, and vehicle, the RTK baseline lengths were approximately 16 km, 11 km, and 12 km, respectively. At this baseline length, multi-system RTK can achieve ambiguity fixing in 1 to 2 epochs, and once the ambiguity is successfully fixed, RTK positioning accuracy can reach centimeter to millimeter levels[29]. Taking the longest baseline (16 km) drone scenario as an example, this paper calculates the RTK ADOP (ambiguity precision factor) value to evaluate the ambiguity fixing performance. The smaller the ADOP value, the higher the ambiguity fixing success rate: ADOP values less than 0.12 indicate an ambiguity fixing success rate greater than 99.9%; ADOP values less than 0.14 indicate an ambiguity fixing success rate greater than 99.0%[29]. As shown in Figure 4, the first epoch ADOP value is 0.13, the second epoch ADOP value is 0.09, and subsequently, the ADOP value gradually decreases with filtering. It can be seen that in this scenario (16 km), RTK can successfully achieve ambiguity fixing in 1 to 2 epochs, while the other two scenarios have shorter RTK baselines, resulting in better ambiguity fixing performance. Therefore, the RTK results in this paper meet the conditions to serve as a benchmark.
 |
| Figure 4 ADOP Value of Airborne RTK (16 km)Fig. 4 ADOP value of airborne RTK (16 km) |
|
Figure Options |
Table 3 lists the PPP-RTK data strategies configured in the NASDAK software during this experiment. Reference [21] points out that based on the PPP-RTK method in this paper, the various products of the server are coupled with each other. Although the precision of any single product is relatively poor during the filtering initialization stage, the precision of the combined product can reach millimeter level, consistent with the precision of phase observations. Therefore, the server products can be used at the beginning of filtering without needing to reinitialize across days. When the user side utilizes the server products for corrections, it also considers the product precision information output by the server. The server performs multi-station joint computation, with numerous ambiguity parameters, and even with partial ambiguity fixing, there is a risk of incorrect fixing. Once any ambiguity is incorrectly fixed, it will affect the positioning of all users. To avoid this risk, the PPP-RTK server in this paper adopts a floating-point ambiguity solution. Reference [30] theoretically proves that using the floating-point product from the server allows the user to achieve rapid high-precision positioning. The user side adopts the LAMBDA algorithm for partial ambiguity fixing[31]. The DIA (detection, identification, and adaptation) quality control strategy is used for cycle slip detection and gross error detection and removal[32].
Table 3 PPP-RTK Data Processing StrategiesTab. 3 PPP-RTK data processing strategies
| Item | Strategy |
| Observations | GPS (G) L1/L2, BDS2/3 (C2/3) B1I/B3I, GLONASS (R) L1/L2 |
| Random Model | GPS code/phase observation precision: 0.3/0.003 m, G/C2/C3/R system weight ratio 2:1:2:1 |
| Satellite Cutoff Elevation Angle/(°) | 8 |
| Receiver Clock Bias | White noise estimation |
| Satellite Clock Bias | Server: white noise estimation; User side: product correction considering precision information |
| Tropospheric Delay | Server: UNB3 m corrects the tropospheric dry delay, using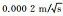 random walk estimation for tropospheric wet delay, with the projection function being GMF; User side: product correction considering precision information random walk estimation for tropospheric wet delay, with the projection function being GMF; User side: product correction considering precision information |
| Ionospheric Delay | Server: white noise estimation; User side: product correction considering precision information |
| Receiver Pseudorange and Phase Bias | Time-invariant parameters |
| Satellite Pseudorange and Phase Bias | Server: time-invariant parameters; User side: product correction considering precision information |
| Phase Ambiguity | Server: arc segment constant estimation; User side: arc segment constant estimation and partial ambiguity fixing |
| Station Position | Server: fixed; User side: dynamic estimation |
| Quality Control | DIA |
Table Options
4.2 Unmanned System Applications
On May 13, 2021, the PPP-RTK positioning terminal was mounted on a six-rotor drone for flight positioning tests along a preset trajectory. Figure 5 shows the drone equipped with the PPP-RTK positioning terminal and its flight trajectory. It can be seen that the flying environment is open, and the observation conditions are good, with the PPP-RTK terminal’s positioning trajectory being continuous and clear, consistent with the preset flight trajectory.
 |
| Figure 5 The Drone Equipped With A PPP-RTK Prototype Terminal And Its Flight TraceFig. 5 The drone equipped with a PPP-RTK prototype terminal and its flight trace |
|
Figure Options |
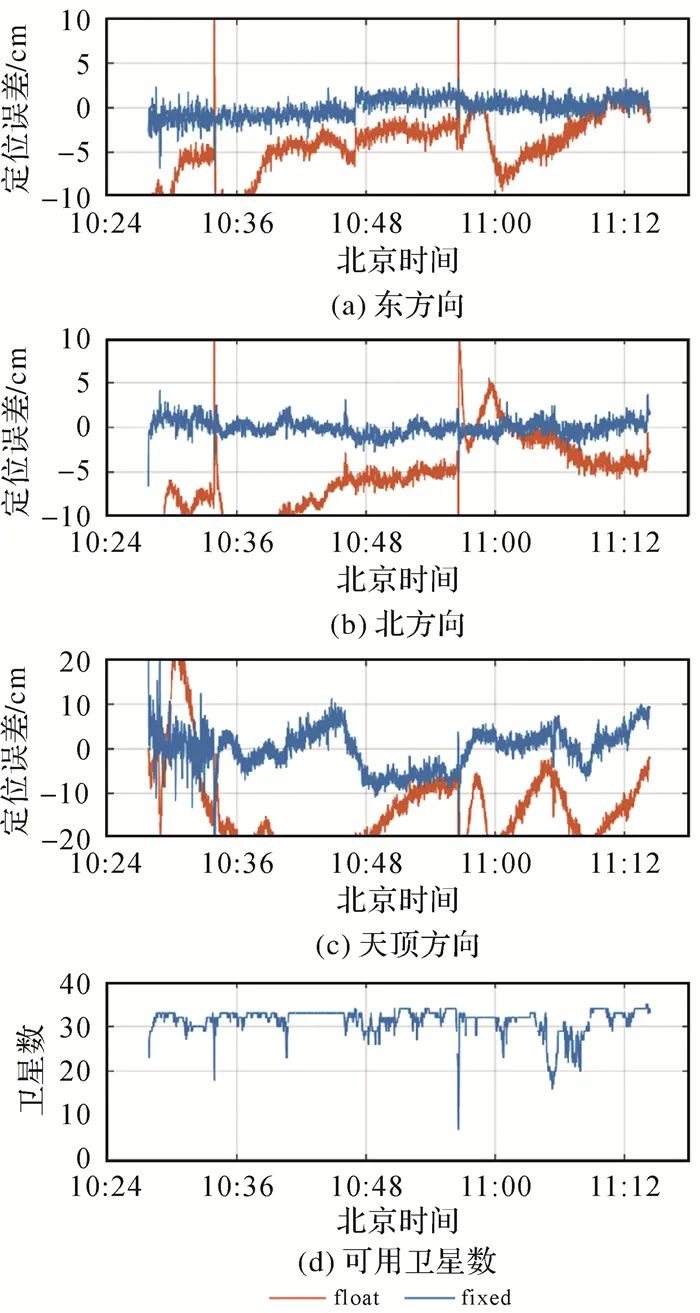
To further evaluate the positioning performance of the drone, a reference station GUDN was set up near the testing area for short baseline (approximately 16 km) RTK positioning, and its results were used as reference values for comparison with PPP-RTK results. Figure 6 shows the positioning error of the drone’s PPP-RTK results relative to the RTK results. From the floating-point solution, it can be seen that if ambiguity fixing is not performed, the positioning error takes a long time to converge, especially in the East direction, where it takes about 1.5 hours to converge within 5 cm. This convergence process is very similar to that of PPP, where the positioning error slowly converges near zero. After ambiguity fixing, the positioning terminal can control the horizontal and vertical positioning errors within 5 and 10 cm, respectively, immediately after being turned on, which fully demonstrates the benefits of ambiguity fixing and also proves the advantages of the PPP-RTK technology over the PPP technology. In addition, numerous studies have also pointed out[12] that the improvement in convergence in the East direction due to ambiguity fixing is particularly significant, and the results in this paper reflect this point. The rapid ambiguity fixing is also attributed to the joint use of multi-system data, with the number of available satellites across the entire experiment period generally ranging from 25 to 30.
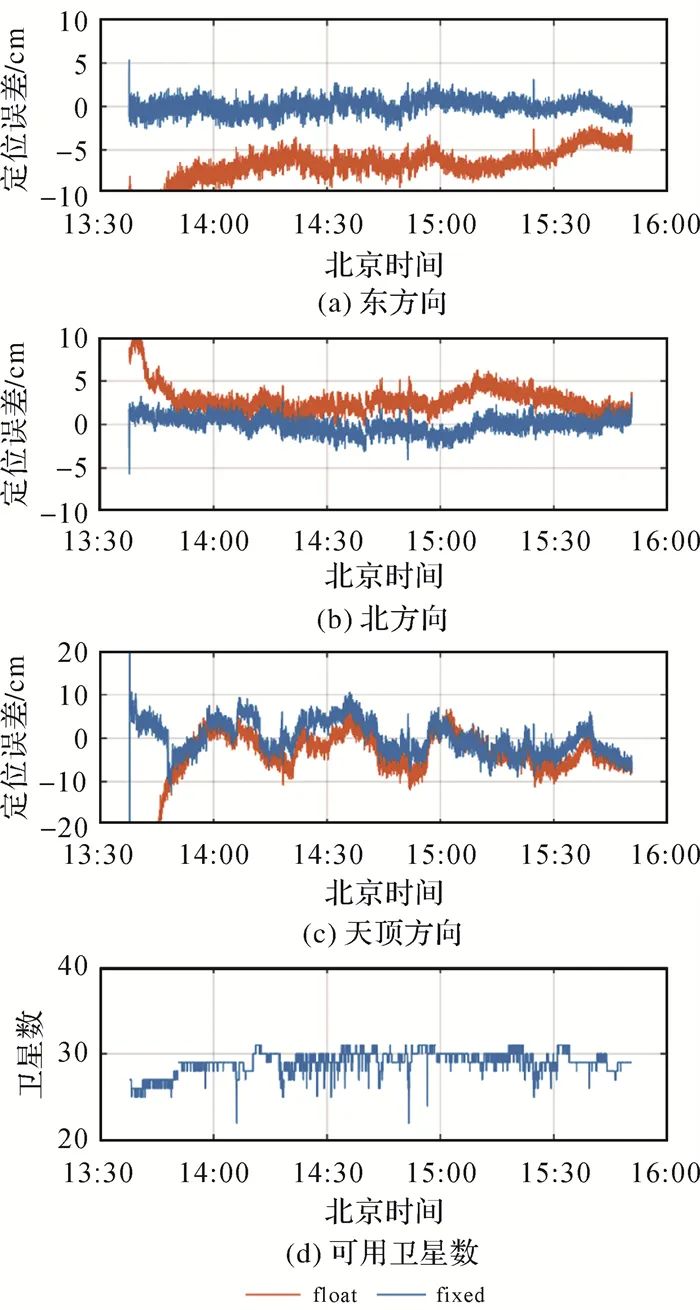 |
| Figure 6 Positioning Errors And Number Of Satellites For Airborne PPP-RTKFig. 6 Positioning errors and number of satellites for airborne PPP-RTK |
|
Figure Options |
Table 4 quantitatively presents the first ambiguity fixing time (TTFF), ambiguity fixing success rate, and root mean square error (RMS) for the drone PPP-RTK. In this paper, TTFF refers to the time for ambiguity fixing to pass the FFRatio test[33] and for the positioning results to meet the horizontal and vertical positioning errors of 5 and 10 cm, respectively, and to maintain for at least 20 epochs. The ambiguity fixing success rate refers to the ratio of the number of epochs that pass the FFRatio test and meet the horizontal and vertical positioning errors of 5 and 10 cm to the total number of epochs. The results show that the TTFF for the drone PPP-RTK is 5 seconds, with an ambiguity fixing success rate of 99.79%, and horizontal positioning accuracy of about 1 cm, while the vertical positioning accuracy is 3.82 cm.
Table 4 TTFF, Success Rate Of Ambiguity Resolution (AR), And RMS Of Airborne, Tractor-Borne And Vehicle-Borne PPP-RTKTab. 4 TTFF, success rate of ambiguity resolution (AR), and RMS of airborne, tractor-borne and vehicle-borne PPP-RTK
| Test Scenario | TTFF/s | AR Success Rate/(%) | RMS/cm | ||
| E | N | U | |||
| Drone | 5 | 99.79 | 0.81 | 0.95 | 3.82 |
| Agricultural Machinery | 2 | 99.14 | 0.95 | 0.71 | 4.07 |
| Vehicle | 7 | 98.96 | 1.06 | 0.84 | 4.33 |
Table Options
4.3 Smart Agriculture Applications
To evaluate the service performance of PPP-RTK in smart agriculture, a PPP-RTK test was conducted on agricultural machinery in Miyun, Beijing, on May 20, 2021. Since Miyun is close to the MYKT reference station, the server computation for this experiment did not use this station but treated it as a short baseline (approximately 11 km) RTK reference station. As shown in Figure 7, the PPP-RTK terminal and measuring antenna were mounted on agricultural machinery, which drove along a preset trajectory. Throughout the measurement section, except for some low buildings blocking the signal, the entire measurement area was open. The total duration of the measurement section was approximately 2 hours, during which the instrument was cold-started twice, with three segments of agricultural machinery testing lasting approximately 35 minutes each.
 |
| Figure 7 The Agricultural Tractor Equipped With A PPP-RTK Prototype Terminal And Its TraceFig. 7 The agricultural tractor equipped with a PPP-RTK prototype terminal and its trace |
|
Figure Options |
Figure 8 shows the positioning error of the agricultural machinery PPP-RTK relative to the number of satellites. It can also be seen that the floating-point solution converges slowly while the fixed solution initializes instantly. The floating-point solution takes about 10 to 20 minutes to converge, while the fixed solution achieves second-level convergence. From the geographical location of MYKT in Figure 3, it can be seen that the testing location is already at the edge of the reference network, yet it still achieves rapid high-precision positioning, thanks to the undifferenced and uncombined PPP-RTK simultaneously estimating all parameters and conducting global modeling. The observation conditions at the testing site were also good, with most epochs observing around 30 satellites, except for a few epochs where only about 21 satellites were observed.
|
|
| Figure 8 Positioning Errors And Number Of Satellites For Tractor-Borne PPP-RTKFig. 8 Positioning errors and number of satellites for tractor-borne PPP-RTK |
|
Figure Options |
The positioning performance of the agricultural machinery PPP-RTK is quantitatively evaluated in Table 4. The average TTFF for the three cold starts of PPP-RTK was 2 seconds, with an ambiguity fixing success rate of 99.14%, and horizontal positioning accuracy still at around 1 cm, while vertical positioning accuracy was 4.07 cm. Comparing the results of the drone PPP-RTK in Table 4, it can be observed that under the same open observation conditions, the positioning performance of the terminal prototype is basically consistent, reflecting its stable service capability.
4.4 Intelligent Driving Applications
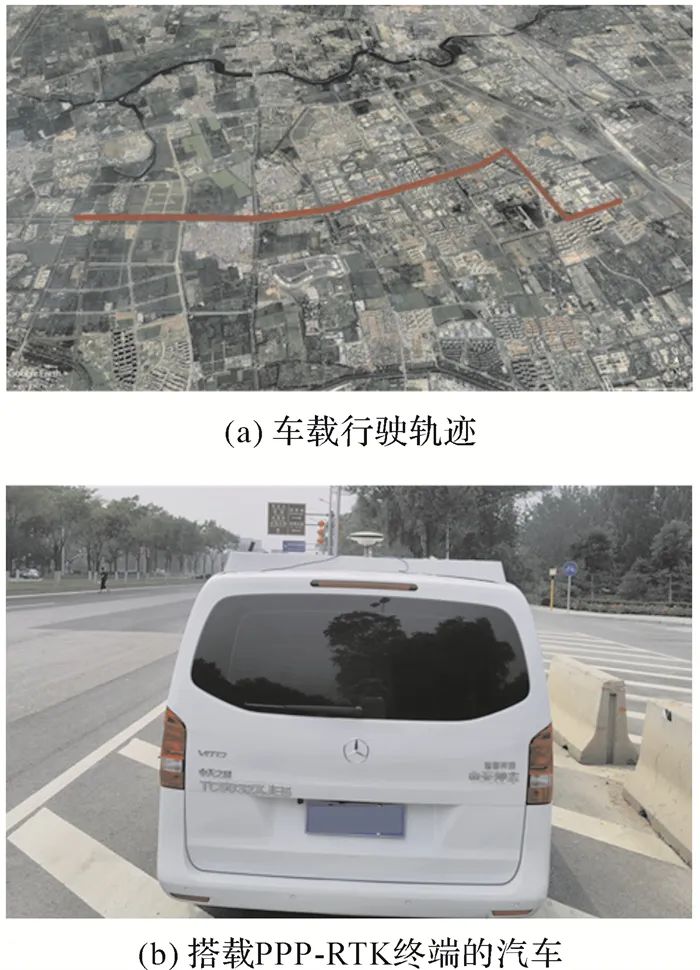
On June 29, 2021, the author tested the positioning effect of the vehicle-mounted PPP-RTK positioning terminal in an urban environment, specifically on the Beiqing Road section in Haidian District, Beijing, where there are fewer high-rise buildings. The test lasted approximately 40 minutes, with the vehicle speed ranging from 40 to 60 km/h. Figure 9 shows the test vehicle and its trajectory. From the surrounding environment of the trajectory, it can be seen that this area does not belong to the main urban area, with minimal obstruction and good observation conditions.
|
|
| Figure 9 The Car Equipped With A PPP-RTK Prototype Terminal And Its Driving TrajectoryFig. 9 The car equipped with a PPP-RTK prototype terminal and its trace |
|
Figure Options |
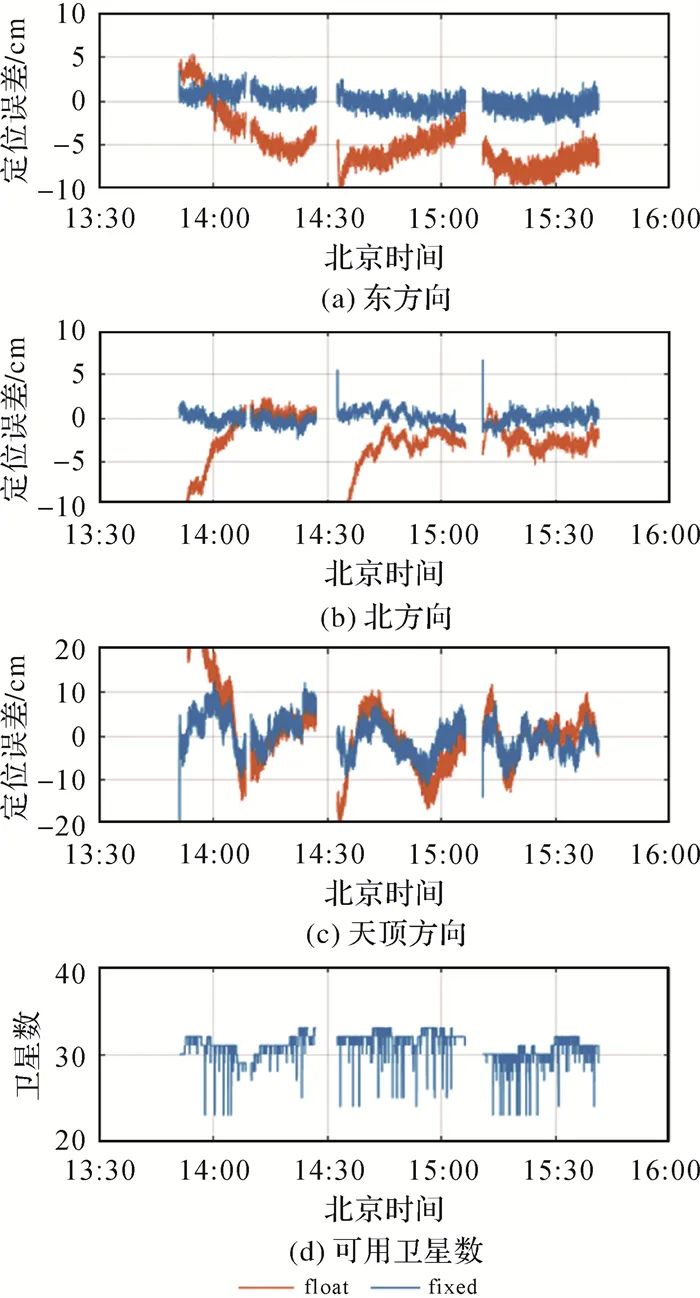
Figure 10 shows the positioning error of the vehicle-mounted PPP-RTK relative to the short baseline RTK. In this test, the short baseline RTK reference station remained GUDN, which is within 12 km of the dynamic vehicle. The floating-point positioning results still require long convergence times and exhibit two instances of re-convergence, which is due to the vehicle passing under a pedestrian overpass at that moment, resulting in weak satellite signals. As can be seen from the number of satellites, the number of satellites suddenly decreased at that moment. Regarding the fixed solution, although the satellites re-acquire tracking after losing lock, it can still quickly fix the ambiguity again and achieve high-precision positioning. The vertical error of the vehicle-mounted PPP-RTK fluctuated significantly in the first few minutes, mainly because the reference station TJJC, which is located near the vehicle testing area, experienced a data interruption during this period, which did not participate in product computation. The data interruption of this station affected the quality of ionospheric products, ultimately impacting the vertical positioning results.
|
|
| Figure 10 Positioning Errors And Number Of Satellites For Vehicle-Borne PPP-RTKFig. 10 Positioning errors and number of satellites for vehicle-borne PPP-RTK |
|
Figure Options |
Table 4 shows that the TTFF for the vehicle-mounted PPP-RTK is 7 seconds, with an ambiguity fixing success rate of 98.96%, and horizontal positioning accuracy still around 1 cm, while vertical positioning accuracy is 4.33 cm. Comparing with the previous results, the vehicle positioning success rate is lower than that of the airborne and agricultural machinery scenarios, which is due to the more complex and variable testing environment of the dynamic vehicle.
5 Summary And Outlook
The undifferenced and uncombined PPP-RTK conforms to the development trend of multi-frequency and multi-GNSS, with synchronous estimation of all parameters possessing global optimality. This paper constructs CDMA and FDMA PPP-RTK models from theory to practice and develops corresponding software, while also embedding the terminal software into the ARM Cortex-A8 chip-based OK335 core board, developing a PPP-RTK positioning terminal prototype. To evaluate the performance of this PPP-RTK positioning terminal in practical application scenarios, the positioning terminal was mounted on drones, agricultural machinery, and urban cars for real-time tests based on the precise server products estimated from the Beijing-Tianjin-Hebei reference network with an average station spacing of 154 km. The results and conclusions are as follows:
(1) The TTFF for the drone PPP-RTK is 5 seconds, with an ambiguity fixing success rate of 99.79%, and horizontal positioning accuracy of about 1 cm, while vertical positioning accuracy is 3.82 cm. The TTFF for the agricultural machinery PPP-RTK is 2 seconds, with an ambiguity fixing success rate of 99.14%, and horizontal positioning accuracy still at around 1 cm, while vertical positioning accuracy is 4.07 cm. The vehicle-mounted PPP-RTK has a slightly lower ambiguity fixing success rate of 98.96% due to the more complex testing environment, but it can still achieve the first ambiguity fixing within 7 seconds, with horizontal accuracy still reaching 1 cm and vertical positioning accuracy of 4.33 cm. Additionally, the floating-point solutions for the three experiments require a long time (from tens to over twenty minutes) to converge, which proves the benefits of ambiguity fixing and the advantages of PPP-RTK technology over PPP technology.
(2) From the experimental results of the three scenarios, with the joint use of multi-system data in relatively open environments, the self-developed undifferenced and uncombined PPP-RTK positioning terminal can achieve second-level ambiguity fixing, with true dynamic positioning accuracy reaching horizontal 1 cm and vertical 4 cm. In cases of satellite loss of lock and filter restart, the ambiguity can still be fixed within seconds, again achieving high-precision positioning, demonstrating that the self-developed PPP-RTK terminal can provide continuous and reliable positioning results.
(3) This paper has initially developed a PPP-RTK positioning terminal prototype, but there are still many issues to be resolved for the PPP-RTK technology to progress from theory to mature application. For example, how to further reduce the computational and memory burdens of terminal devices, and how to embed PPP-RTK terminal algorithms into lighter and more compact devices, will be the focus of our future research and development.
Author Introduction
Author Introduction:
First Author Introduction:Zhang Baocheng (1985—), Male, Researcher, research direction is multi-frequency and multi-mode GNSS undifferenced and uncombined PPP-RTK. E-mail:[email protected]
First Author Introduction:Zhang Baocheng (1985—), Male, Researcher, research direction is multi-frequency and multi-mode GNSS undifferenced and uncombined PPP-RTK. E-mail:[email protected]
Initial Review: Zhang Yanling
Re-review: Song Qifan
Final Review: Jin Jun
Final Review: Jin Jun

Previous Recommendations
News
○ Live Broadcast Announcement | 65th Anniversary Academic Report of the Journal of Geodesy (Seventh Session)
○ Collaborative Precision Positioning | Huang Dingfa: Grid-based VRS Technology for High-Precision Real-Time Positioning Services
○ Recruitment of Public Institutions Affiliated to the Henan Provincial Department of Natural Resources in 2022 (Including Surveying, Geographic Information, Remote Sensing Related Majors)
○ Notice on Soliciting Drafting Units for Series Group Standards on Cost Elements of Surveying and Geographic Information Technology Services
○ Comprehensive Performance of China’s Meteorological Satellites Reaches World Advanced Level丨Extraordinary Decade