1. Introduction
This is a module for signal acquisition and computation built a couple of days ago using the H7B0 microcontroller, which uses its 16-bit ADC to capture signals and perform spectrum analysis, with results displayed on an OLED screen. Calculating a 2048-point FFT takes about 10 milliseconds. Next, let’s test if the computation speed can be improved using the FFT from the DSP algorithm library in CMSIS within Cortex, and compare the precision of the results.

2. Adding DSP Library
First, click the Package button in the Keil compilation environment to open the package management unit. Add the Core and DSP packages from CMSIS. After confirming, you can see the corresponding DSP package in the project files.
 In the project options on the C++ settings page, add the constant ARM_MATH_CM7, indicating the use of the DSP algorithm library for the Cortex-M7 core. In the application C file, include the corresponding header files; here, we add two header files. Note that if the definition of the constant ARM_MATH_CM7 is not added before including the header files, compilation errors will occur. Now you can apply the corresponding DSP functions.
In the project options on the C++ settings page, add the constant ARM_MATH_CM7, indicating the use of the DSP algorithm library for the Cortex-M7 core. In the application C file, include the corresponding header files; here, we add two header files. Note that if the definition of the constant ARM_MATH_CM7 is not added before including the header files, compilation errors will occur. Now you can apply the corresponding DSP functions.
3. Calculation Results
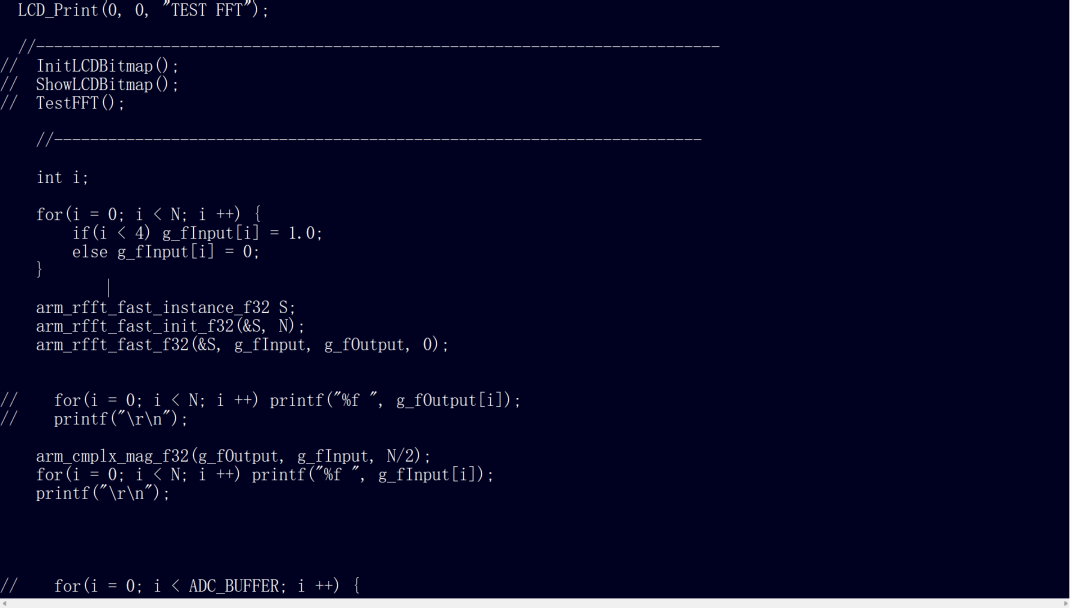
Call the real-valued floating-point FFT function in DSP, initialize a floating-point array of length 2048, setting the first four numbers to 1 and the others to 0. Initialize the FFT instance parameters for the real FFT transformation and assign the FFT results. Display results and plot images.
This is the waveform of the FFT data, where the first 4 data points have an amplitude of 1, and the others are 0. In the transformation result, the first half represents the amplitude spectrum of the data. For real numbers, the amplitude spectrum is symmetric about the center point. The output only provides the first half of the results, while the second half is not computed. It should be noted that FFT computation is in-place storage, meaning the final results are stored in the input data storage area. The output results only show the first half of the actual frequency spectrum, and the second half is conjugate symmetric to the first half.
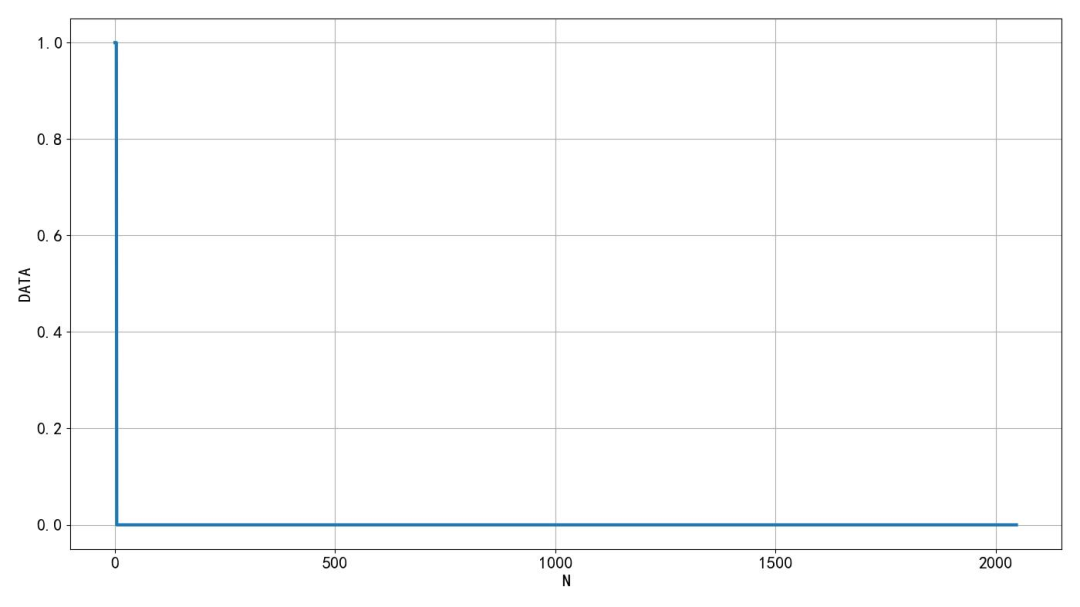
▲ Figure 1.3.1 Waveform of the signal
▲ Figure 1.3.2 Amplitude spectrum after transformationComparing the amplitude spectrum calculated by the microcontroller DSP library with that computed by Python, they overlap. The corresponding error should reflect the differences between single-precision and double-precision floating-point numbers.
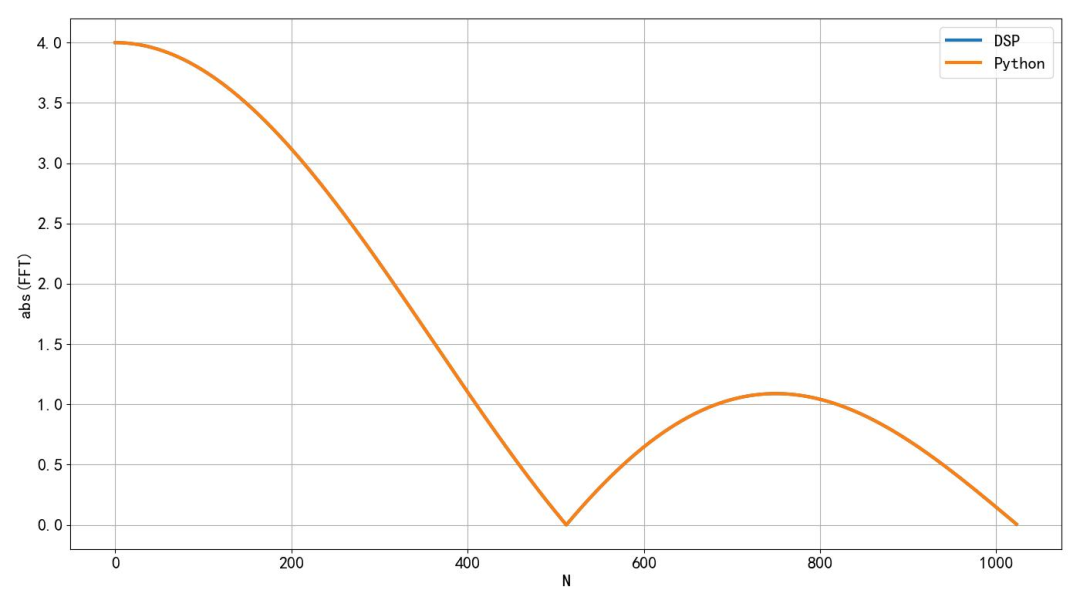
▲ Figure 1.3.3 Results of DSP and Python calculations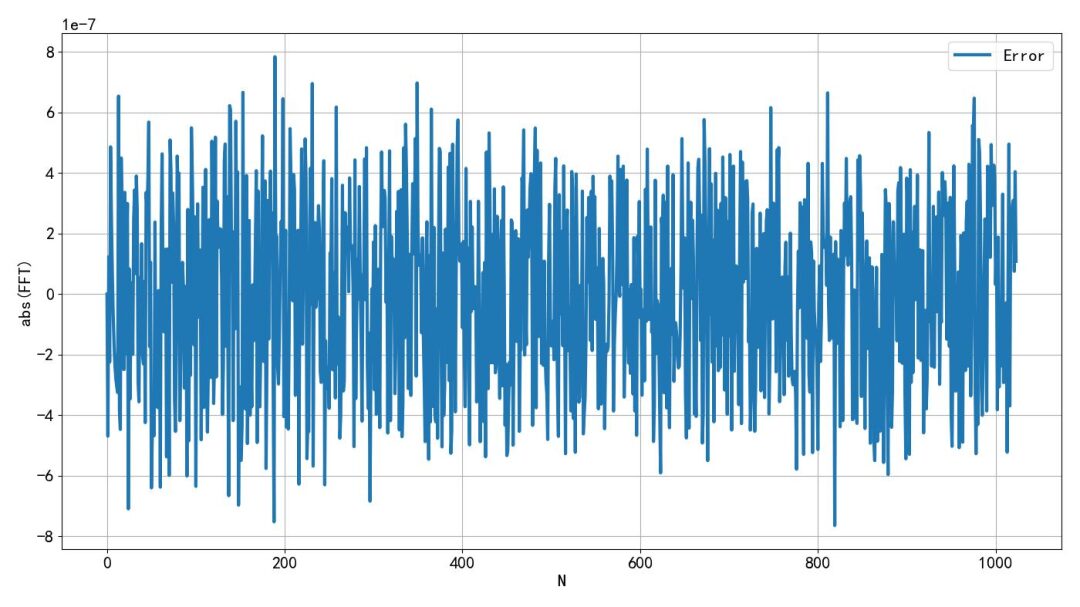
▲ Figure 1.3.4 Error in amplitude calculation between DSP and PythonHowever, a strange situation arose: if the data window length is set to 5, the first value of the DSP calculation exhibits a significant error. The first number reflects the DC component of the data. The same large error occurs when the data window length is 7. This is strange; the results are accurate when the window length is even, but inaccurate when odd. This issue has puzzled me for a long time; I wonder if anyone can provide an explanation.
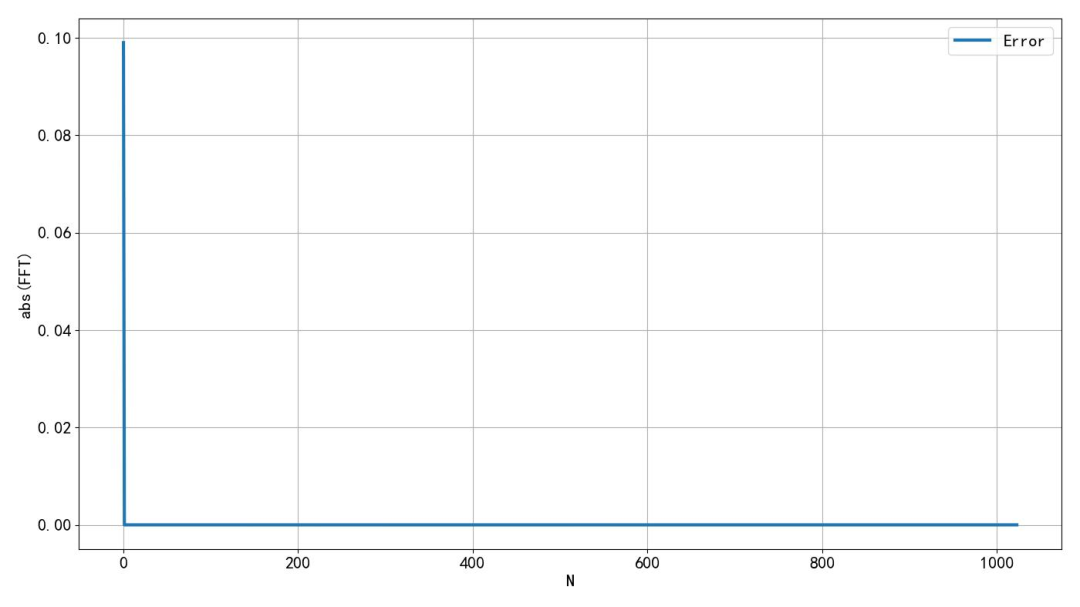
▲ Figure 1.3.5 When the data window width is 5, the first result, the DC component, has a significant errorPlotting the errors corresponding to the first data point from the DSP algorithm library as the data window width varies from 0 to 2048 shows that as the length of the data increases, the error decreases. The error is inversely proportional to the length of the data. When the window is even, the error is 0; when odd, discrepancies arise. This is indeed puzzling.
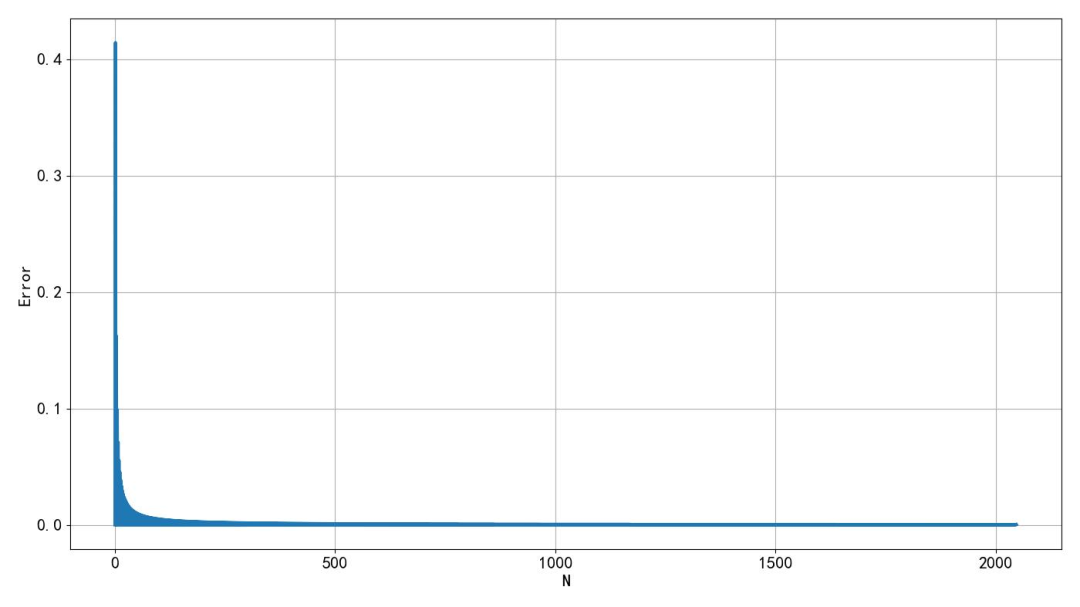
▲ Figure 1.3.6 Error distribution of the DC component calculated with different windows4. Calculation Speed
To measure the FFT computation speed in DSP, operations on the microcontroller port are added before and after the FFT function call, with the high and low levels of the microcontroller port indicating the FFT computation time. By using an oscilloscope to measure the waveform of this port, the computation speed of the FFT in the DSP library can be determined. The microcontroller clock frequency is set to 280MHz, and for a length of 2048 FFT, the computation time is 1.22ms. A custom FFT C language algorithm I wrote a couple of days ago also took about 10ms for the same length. The algorithm efficiency in the DSP library is indeed very high.
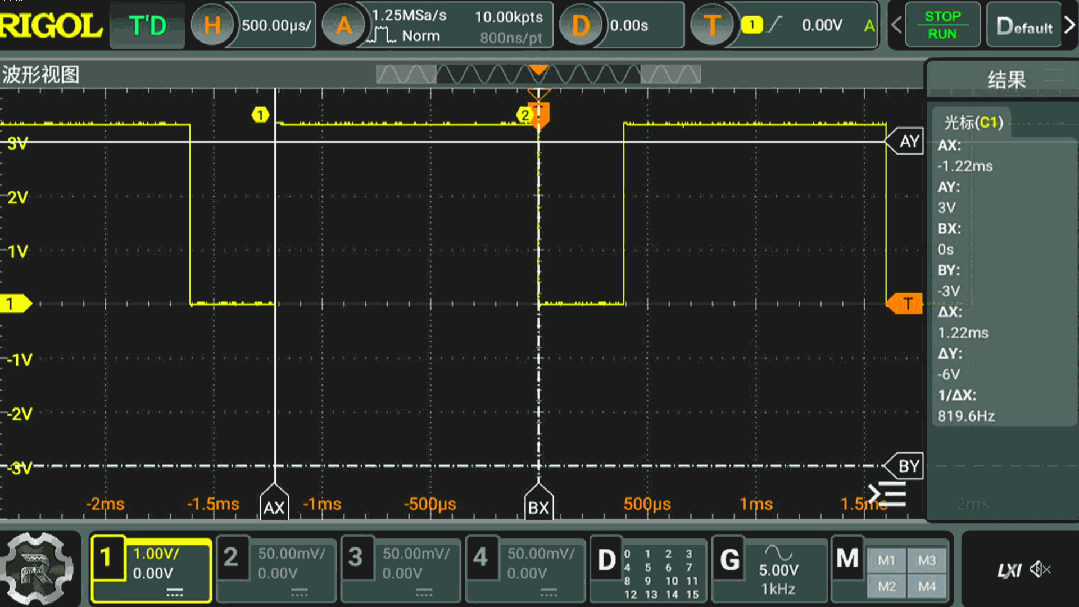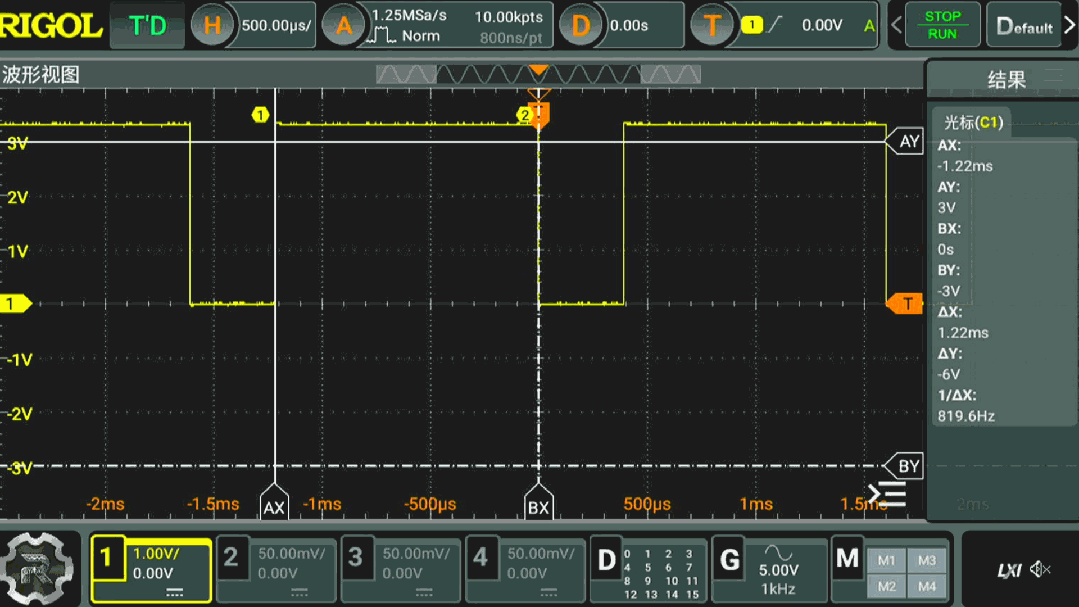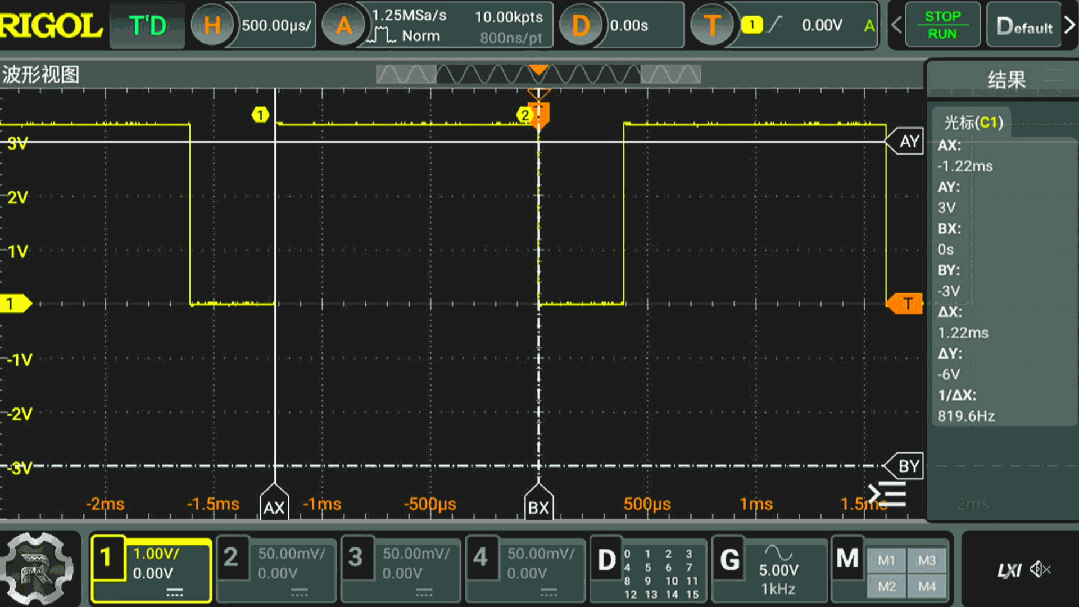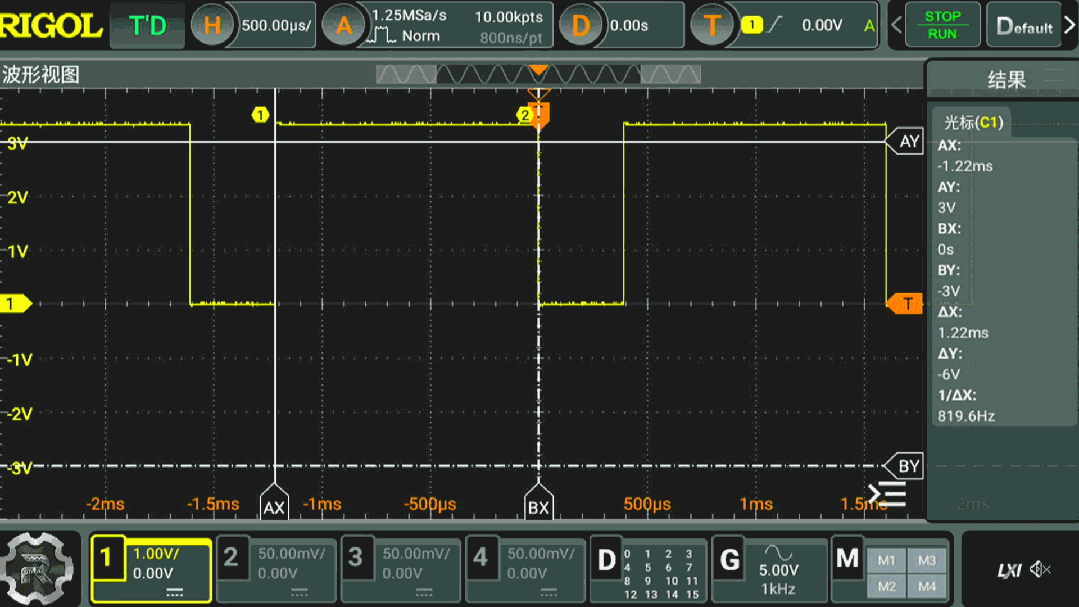
▲ Figure 1.4.1 Calculation speed※ Conclusion ※
This article tests the FFT computation using the DSP algorithm library on the STM32H7B0 microcontroller. The speed is very fast, taking about 1.2ms for single-precision floating-point calculation of 2048 data points, measured at a core clock frequency of 280MHz. However, a puzzling situation arises where the DC calculation shows errors in certain scenarios. The specific reasons are still unclear.

Usage of STM32 DSP Library: https://blog.csdn.net/u010058695/article/details/112665306
[2]Acquisition of Analog Signals and Displaying Spectrum: STM32H7B0: https://zhuoqing.blog.csdn.net/article/details/136419754
[3]Circuit Diagram of STM32H7B0 Module: https://zhuoqing.blog.csdn.net/article/details/136285749