
The generation of images is the result of the interaction between electronics and optics, while the noise in images is objectively present due to the granular nature of the imaging process. Different types of noise arise from various perspectives, each with its characteristics. Therefore, effectively removing noise from images to obtain higher quality images is practically significant. Currently, there are various image denoising methods, including those based on spatial domain, transform domain, partial differential equation models, and morphology. Generally, the typical process of image denoising includes the following steps:
-
Determine the Noise Model: First, based on the actual image situation, identify the mathematical model of the noise, which helps to understand and model the characteristics of the noise.
-
Estimate Parameters: Estimate the necessary parameters in the noise model, which will be used in subsequent steps to select appropriate denoising methods.
-
Select Denoising Method: Choose an appropriate denoising method based on the type of noise. Common methods include spatial domain methods, transform domain methods, partial differential equation model methods, and morphological methods.
-
Measure Evaluation: Finally, assess the effectiveness of the image denoising. This can be achieved by comparing the differences between the denoised image and the original image.
Based on common noise types, this chapter will focus on the wavelet analysis method for image denoising based on the transform domain. Wavelet transform has the advantage of providing effective representation in the time-frequency domain, thus being widely used in image denoising. By analyzing and processing images in the wavelet domain, it is possible to better preserve the structural information of the image while removing noise.
02.Simulating Noise Generation
clc;clear;close all;
% Add Gaussian white noise, salt and pepper noise, and multiplicative noise to the original image. The image is sourced from reference [11]
f=imread('Fig4-1(a)original_pattern.tif');
m=64/255;var = 400/255^2;
g_gauss=imnoise(f,'gaussian',m,var);
d = 0.05;%d represents the noise intensity
g_salt = imnoise(f,'salt & pepper',d);
v = 0.06;
g_speckle = imnoise(f,'speckle', v);
% Display noisy images
figure
subplot(2,2,1), imshow(f),title('Original Image');
subplot(2,2,2), imshow(g_gauss), title('Gaussian Noisy Image');
subplot(2,2,3), imshow(g_salt), title('Salt and Pepper Noisy Image');
subplot(2,2,4), imshow(g_speckle), title('Speckle Noisy Image');
%Image storage
% imwrite(g_gauss,'Fig4-1(b)Nguass.jpg','jpg');
% imwrite(g_salt,'Fig4-1(c)Nsalt.jpg','jpg');
% imwrite(g_speckle,'Fig4-1(d)Nspeckle.jpg','jpg');
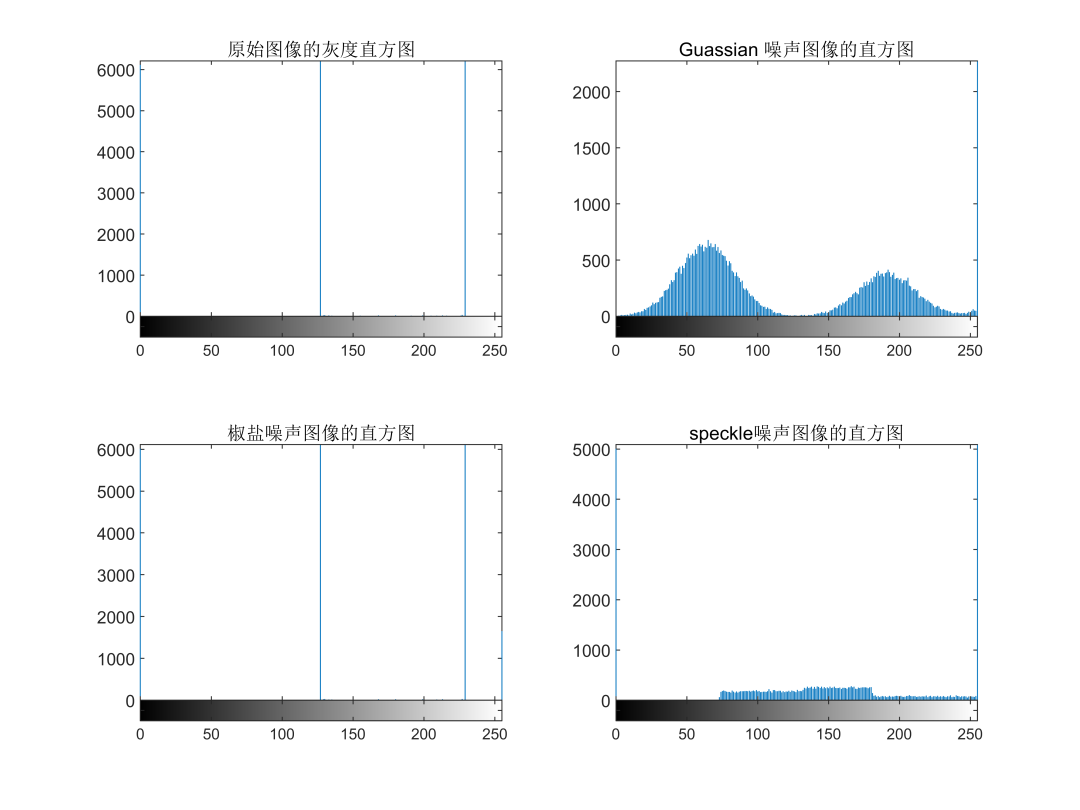
%Display histogram
figure(2)
subplot(2,2,1), imhist(f),title('Grayscale Histogram of Original Image');
subplot(2,2,2), imhist(g_gauss),title('Histogram of Gaussian Noisy Image');
subplot(2,2,3), imhist(g_salt),title('Histogram of Salt and Pepper Noisy Image');
subplot(2,2,4), imhist(g_speckle),title('Histogram of Speckle Noisy Image');
03.Wavelet-Based Denoising Method
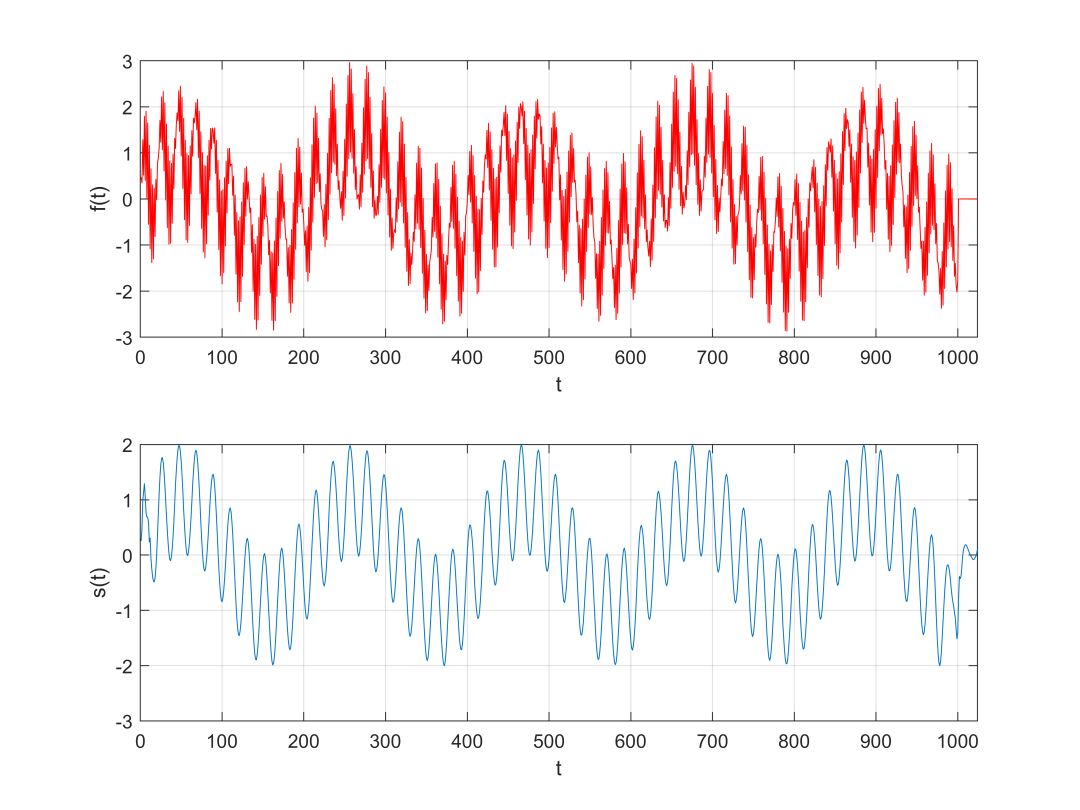
1. Denoising Algorithm Effect Diagram Based on Modal Maximum
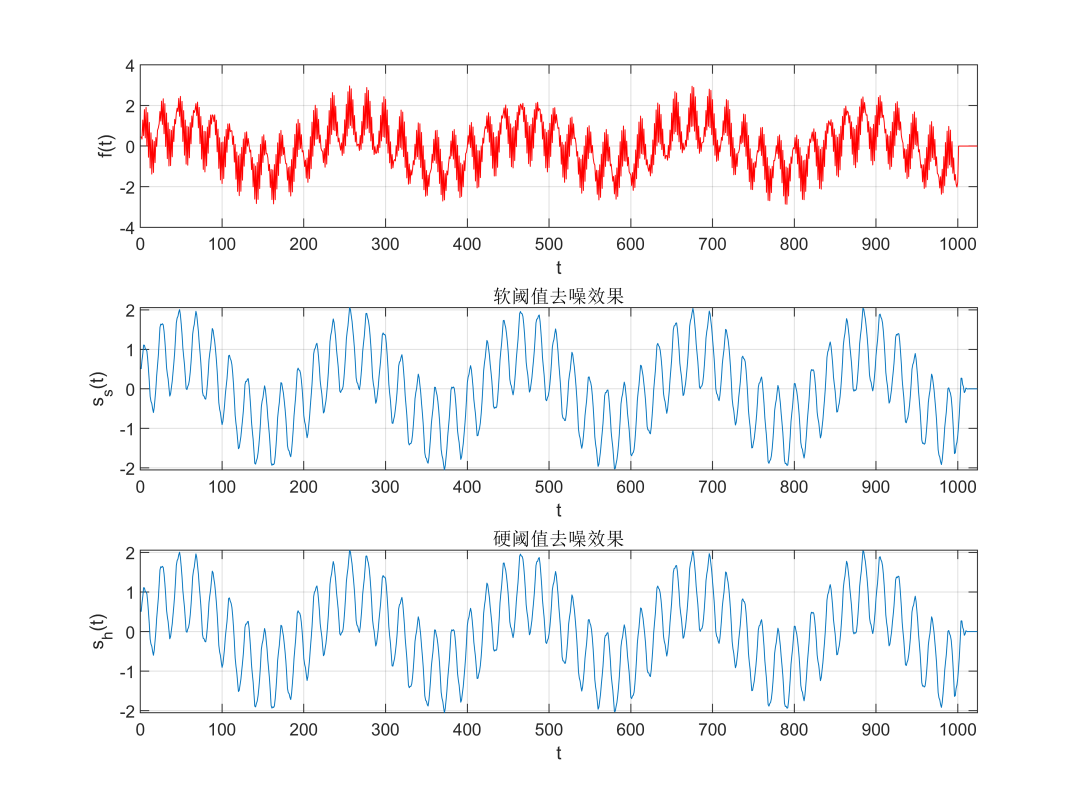
2. Denoising Algorithm Effect Diagram Based on Wavelet Thresholding (Soft and Hard Threshold)
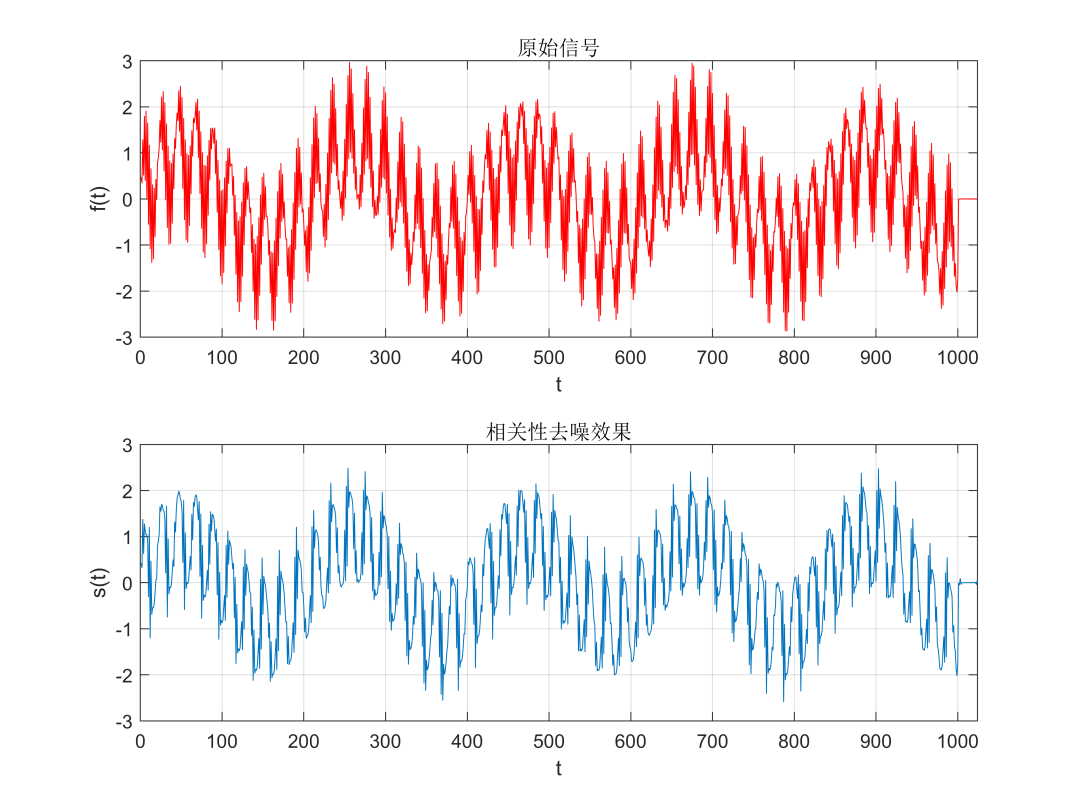
3. Correlation Denoising Effect
Code collection download link: https://mbd.pub/o/bread/ZZ6YmJ9u
Or click “Read the original text” to get the code!

END