Statement: This is a personal learning record.
Mathematical Knowledge:
Gregory-Leibniz Formula
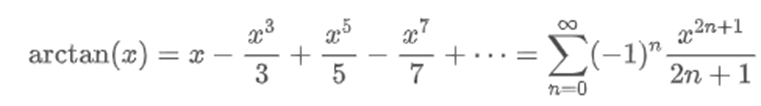
Let x=1, we get
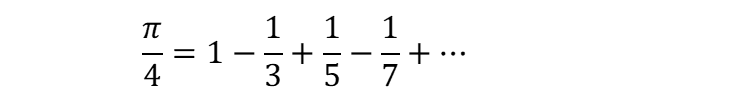
Using the Gregory-Leibniz formula, to find the approximate value of π, we require the absolute value of the last term to be less than 10-6.
[Example 1]
Problem: Write a program to calculate and output the approximate value of π according to the formula π/4≈1−1/3+1/5−1/7+… until the absolute value of a term is found to be less than 10-6 (that term is not added).
Analysis: The right-hand side of the equation in the problem has a denominator that is an arithmetic sequence with a common difference of 2, and the signs alternate. We will use a WHILE loop to construct the right-hand side of the formula until we reach the required precision for the last term.
Using two methods to calculate
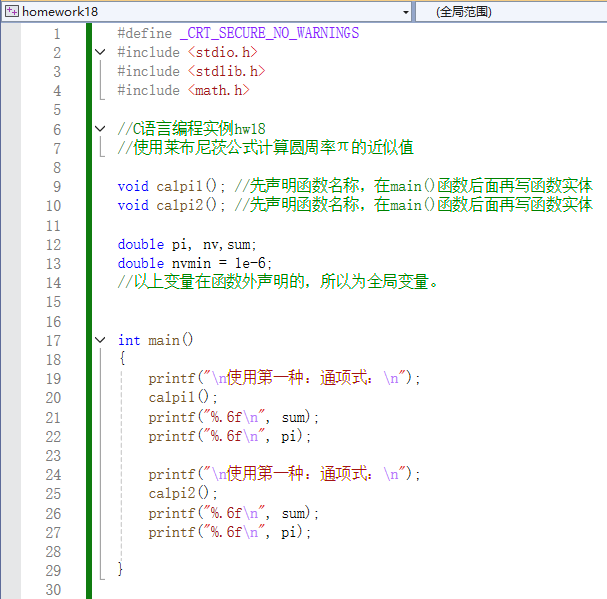


C Code:
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// C Language Programming Example hw18
// Calculate the approximate value of π using the Leibniz formula
void calpi1(); // Declare function name first, then write function body after main()
void calpi2(); // Declare function name first, then write function body after main()
double pi, nv, sum;
double nvmin = 1e-6;
// The above variables are declared outside the function, so they are global variables.
int main()
{
printf(“\nUsing the first method: General term:\n”);
calpi1();
printf(“%.6f\n”, sum);
printf(“%.6f\n”, pi);
printf(“\nUsing the second method: General term:\n”);
calpi2();
printf(“%.6f\n”, sum);
printf(“%.6f\n”, pi);
}
// First method: Using the general term.
void calpi1() {
int i = 1;
double nv;
double flag = 1; // Used for changing the sign of the numerator.
nv = 1;
sum = 0;
while (fabs(nv) > nvmin) {
sum = sum + nv;
i++;
flag = -flag;
nv = flag / (2 * i – 1);
}
pi = 4 * sum;
}
// Second method: Using the recursion method, where the denominator of the next term is the previous term’s denominator + 2.
void calpi2() {
double nv;
double flag; // Used for changing the sign of the numerator.
int fenmu;
sum = 0;
fenmu = 1;
nv = 1;
flag = 1;
while (fabs(nv) > nvmin) {
sum = sum + nv;
flag = -flag;
fenmu += 2;
nv = flag / fenmu;
}
pi = 4 * sum;
}
January 6, 2025