1. Introduction
When dealing with tree structures, it is common to encounter the need to find the Lowest Common Ancestor (LCA) of two nodes. The LCA is defined as the furthest node from the root among all common ancestors of the two nodes in the tree (i.e., the node with the maximum depth). For example, in a family tree, the LCA of two individuals is their lowest common ancestor in terms of generational depth. Tarjan’s algorithm is an offline algorithm that can handle multiple queries in O(n+q) time complexity, where n
is the number of nodes in the tree, and q is the number of queries. Next, we will detail the principles, implementation steps, and code examples of Tarjan’s algorithm for finding the LCA.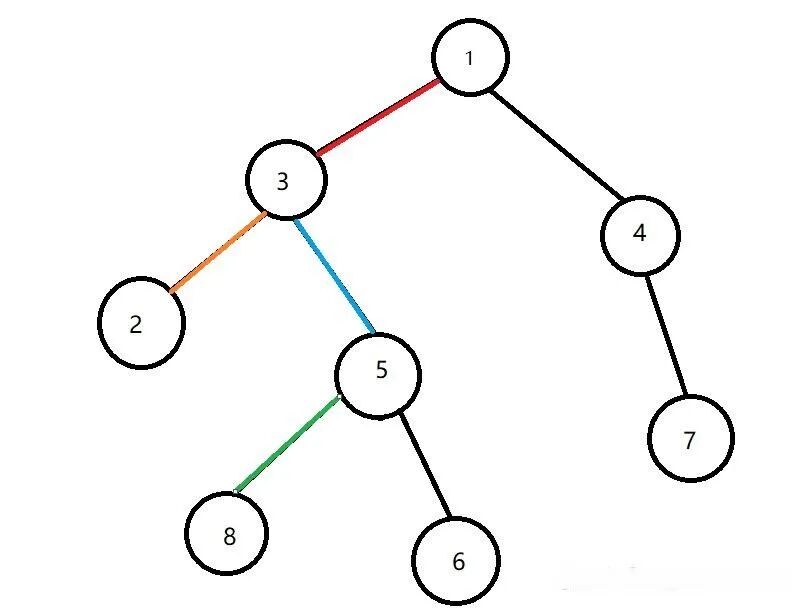
2. Basic Concepts
2.1 Lowest Common Ancestor (LCA)
For two nodes u
and v, their LCA w is defined as the node w that is an ancestor of both u and v, and among all such nodes, w is the furthest from the root. As shown in the figure, the LCA of nodes 2 and 6 is 3.
2.2 Offline Algorithm
An offline algorithm is one that requires collecting all query information before processing all queries at once. In contrast, an online algorithm processes each query immediately upon receipt.
2.3 Union-Find
The Union-Find data structure is used to handle the merging and querying of disjoint sets. In Tarjan’s algorithm, we use Union-Find to maintain the connectivity of nodes and determine whether two nodes belong to the same set.
3. Principles of Tarjan’s Algorithm
Tarjan’s algorithm is based on Depth-First Search (DFS) and Union-Find. The core idea is to merge a node with its parent into the same set after visiting all its child nodes during the DFS process. For each query (u,v), when we visit one of the nodes (assumed to be u), and the other node v has already been visited, we can find the representative element of the set containing v through Union-Find, which is the LCA of u and v.
The specific steps are as follows:
- 1. Initialization: Initialize each node as an independent set and mark all nodes as unvisited.
- 2. Depth-First Search: Start DFS from the root node.
- · Mark the current node as visited.
- · Recursively visit all child nodes of the current node.
- · After visiting a child node, merge the set of that child node with the set of the current node.
- · For all queries (u,v) where the current node is one of the query nodes, if the other node v has already been visited, find the representative element of the set containing v through Union-Find; this representative element is the LCA of u and v (backtrack to the node with the smallest level when checking two nodes).
- 3. End: Once the DFS is complete, all query results have been obtained.
Code:
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
// Union-Find parent array
int parent[MAXN];
// Mark nodes as visited
bool visited[MAXN];
// Store the tree's adjacency list
vector<int> adj[MAXN];
// Store query information
vector<pair<int, int>> queries[MAXN];
// Store query results
int lca[MAXN];
// Initialize Union-Find
void init(int n) {
for (int i = 1; i <= n; ++i) {
parent[i] = i;
visited[i] = false;
}
}
// Find the representative element of the set containing node x
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// Merge the sets containing nodes x and y
void unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
parent[rootX] = rootY;
}
}
// Tarjan's algorithm to find LCA
void tarjan(int u) {
visited[u] = true;
for (int v : adj[u]) {
if (!visited[v]) {
tarjan(v);
unite(v, u);
}
}
for (auto query : queries[u]) {
int v = query.first;
int idx = query.second;
if (visited[v]) {
lca[idx] = find(v);
}
}
}
int main() {
int n, m, root;
cin >> n >> m >> root;
// Read tree edge information
for (int i = 0; i < n - 1; ++i) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
// Read query information
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
queries[u].emplace_back(v, i);
queries[v].emplace_back(u, i);
}
// Initialize Union-Find
init(n);
// Execute Tarjan's algorithm
tarjan(root);
// Output query results
for (int i = 0; i < m; ++i) {
cout << "Query " << i + 1 << ": LCA of " << queries[lca[i]][0].first << " and " << queries[lca[i]][0].second << " is " << lca[i] << endl;
}
return 0;
}5. Complexity Analysis
5.1 Time Complexity
The time complexity of Tarjan’s algorithm is O(n+q), where n is the number of nodes in the tree, and q is the number of queries. This is because the time complexity of the depth-first search is O(n), and each query requires constant time to process.
5.2 Space Complexity
The space complexity is O(n+q), mainly used to store the tree’s adjacency list, query information, and the parent array of the Union-Find structure.
6. Conclusion
Tarjan’s algorithm is an efficient offline algorithm for finding the LCA of multiple pairs of nodes in a tree. By combining depth-first search and Union-Find, it can handle all queries in O(n+q) time complexity. In practical applications, if a large number of queries need to be processed, Tarjan’s algorithm is a good choice.