Click the blue text

Summary of C Language: Basic Data Representation and Operations

Source from the Internet, please delete if infringed

1. Introduction to Data

When defining a variable, it is necessary to specify the type of the variable. Constants are also distinguished by type. Since data is stored in memory units, it exists concretely, and each storage unit has a limited size in bytes, the range of data stored in each storage unit is limited. Therefore, it is necessary to allocate storage units, including the length of the storage unit (the number of bytes occupied) and the form of data storage. Different types of storage are also for the convenience of programmers to operate on data; otherwise, if a bunch of data is placed together, it is unclear which is which. This classification greatly improves programming efficiency.

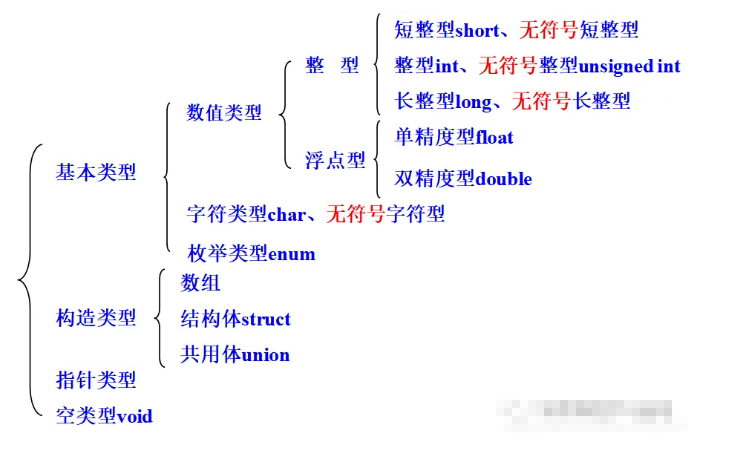
2. Integer Types

Basic Integer int:

The compiler generally allocates 2 or 4 bytes (depending on the compilation environment), 1 byte (8 bits), and integers are stored in the storage unit in the form of two’s complement. For example, 5 in binary is 101; if stored in two bytes, the positive two’s complement and source code are: 0000 0000 0000 0101.

For -5, the source code must be obtained first, then bitwise negated, and finally add 1 to get the negative two’s complement, such as

(source code) 0000 0000 0000 0101

(bitwise negation) 1111 1111 1111 1010 (negative two’s complement) 1111 1111 1111 1011

When storing integers in the storage unit, the leftmost (first bit) is used to represent the sign, where 0 indicates a positive number and 1 indicates a negative number.

Current compilation environments generally allocate 4 bytes (32 bits), with a range from -2^31 to 2^31-1, which is -2147483648 to -2147483647.

Short Integer short int:

Short integers are generally allocated two bytes, with storage similar to int. The system typically allocates 2 bytes (16 bits), and the range of values it can represent is -32768 to 32767 (less than int).

Long Integer long int:

The system allocates 4 bytes (32 bits), so the range of numbers that long integers can represent is -2^63 to 2^63-1. Unlike int, which has at least 2 bytes, long has at least 4 bytes, and sizeof(int) <= sizeof(long int).

In some compilation environments, int is only two bytes.

Long Long Integer long long int:

The system allocates 8 bytes (64 bits), so the range of numbers that long integers can represent is -2^63 to 2^63-1 (much longer than long).

Note: The above refers to a 64-bit system, and it still depends on the specific compilation environment. If on a 32-bit machine or a relatively old compilation environment, the range of representable values and allocated bytes may differ.

Unsigned (Unsigned Type)

In integers, there are signed and unsigned types, where signed is the default. By adding the keyword unsigned before variable definition, integer data can be converted to unsigned type data, which is the absolute value in mathematics. Generally, the default initialization is signed.

Real type data cannot have signed or unsigned modifiers.

Since the highest bit of unsigned data is no longer used to indicate the sign but is used to represent numbers, the storage range of unsigned will be twice that of signed. For example, -1 stored in two bytes in two’s complement form is 1111 1111 1111 1111. The first digit indicates the sign bit, so the value is only 2^15 bits. However, if it is added with unsigned, the first bit will no longer represent the sign, so the value increases to 2^16 bits.

Character Type char:

Character data is stored in memory as follows: each character variable is allocated one byte of space, so a single quote can only hold one character, and character values are stored in storage units in ASCII code format. Characters can be any character, but once a number is defined as a character, it cannot participate in numerical operations. For example, ‘5’ and 5 are different; ‘5’ is a character constant, representing the shape of the symbol ‘5’, which is output as is when needed, and is not stored as a number, so it cannot participate in operations.

char is a special form of int. Generally, char type variables can be defined to operate like int variables.

Integers from 0-127 can be assigned to a character variable. If a negative number is assigned, since the character type can only read one character, the preceding sign will not be read.

Defining a character variable actually defines a one-byte integer variable, which is just used to store characters.

char a = '-6';char b = a;printf("%c", b);//The result is output 6

signed char can represent numeric ranges from -2^7 to 2^7-1, which is -128 to 127.

unsigned char can represent numeric ranges from 0 to 255.

(There is also a string data type, which will be detailed later)

Boolean Type bool:

Before using this type, the preprocessor header file command #include is required, and then the variable can be defined, such as bool a; The value of the boolean type has only two: false (0) and true (1 or any non-zero value). bool only occupies one byte.

_BOOL length depends on the actual environment, generally considered to be 4 bytes (this can be defined without a header file), but the type value has only 0 and 1.

3. Floating Point Type (Real Number Type)

In C language, real numbers are stored in memory in exponential form; a decimal can be represented in many ways, such as 3.14159, which can be represented as 0.0314159*10^2 or 314.159*10^-2, etc.

Since the position of the decimal point can move, it is called a floating-point number. All floating-point type values are stored in memory in binary exponential form, where the decimal part and the exponent part are stored separately.

The storage consists of three parts: sign bit, decimal part, and exponent part represented by powers of 2. The storage method uses scientific notation to store data, such as: 133.5 (in memory) sign bit (0 for positive) exponent (exponent part) mantissa (the number after the decimal point).

For single precision floating-point numbers, the first step is to convert the integer 135 into binary, which is 1000 0101, and then convert the decimal part 5 into 0.1, thus 135.5 in binary is 1000 0101.1.

This represents the mantissa, which must first be expressed in scientific notation; 1000 0101.1 in scientific notation is 1.0000 1011*2^7.

Here the exponent is represented using a biased exponent, with a float offset of 127. The exponent part is 8 bits, so the exponent here is 127 + 7 = 134; converting 134 to binary gives 1000 0110.

Since it is stipulated that the digit before the decimal point is always 1, it will not be stored in the computer, so the mantissa here is 00001011. All trailing zeros are filled to make up 23 bits. Since this is a positive number, the sign bit is 0.

Thus the number is stored in memory as: 0100 0011 0000 0101 1000 0000 0000 0000 (four bytes).

**Due to the limited length of storage units, representing a floating-point number in binary cannot yield a completely accurate value and can only maintain limited precision. The more bits occupied by the decimal part, the more significant figures there are; the more bits occupied by the exponent part, the larger the range of representable values.

**Bias: refers to the encoding value of the exponent field in floating-point representation, which is the actual value of the exponent plus a fixed value. According to the IEEE 754 international standard, this fixed value is 2 raised to the (e-1) power, where e is the length of the unit that stores the exponent (i.e., how many bits) (this determines the maximum range of the exponent part that a floating-point type can represent).

Single Precision Float:

The byte size of single precision floating-point is 4 bytes, with 6-7 effective digits, and a decimal length of 23 bits (24 includes the sign bit). The exponent field is 8 bits, and the fixed bias value is 2 raised to the 7th power minus 1, which equals 127.

(See the range in the figure)

Double Precision Float:

The byte size of double precision floating-point is 8 bytes, with 15 effective digits, and a decimal length of 52 bits (53 includes the sign bit). The exponent field is 11 bits, and the fixed bias value is 2 raised to the 10th power minus 1, which equals 1023.