Introduction:This tutorial provides a step-by-step guide toADC samplingandvarious filtering algorithms. The MCU used in this tutorial isSTM32F103ZET6. Based on theHAL library, this tutorial teaches the ADC sampling function and analyzes and compares the experimental results of various common filters, visually demonstrating the filtering effects withVOFA+tool.
Experimental Effect Diagram:
1. ADC Sampling
1.1 Introduction to ADC
The microcontroller is a digital chip that only recognizes logical sequences composed of 0s and 1s. However, in reality, there are many analog physical quantities in life that are not 0 or 1, such as temperature and humidity. In such cases, AD conversion is often required. The English term for AD conversion is Analog to Digital conversion, which converts analog quantities into digital quantities; similarly, DA stands for Digital to Analog, converting digital quantities back to analog quantities.
ADC, short for Analog to Digital Converter, is a device that can convert external analog signals into digital signals. Using it to read values from I/O ports will no longer yield simple 0s or 1s, but rather continuously variable values. ADC sampling converts continuously varying analog quantities over time into discretely sampled quantities.
Several important parameters of ADC are as follows: (1) Measurement Range: The measurement range for an ADC is similar to the measuring range of a ruler; it determines the output voltage range of the external device connected to it, which must not exceed the ADC's measurement range (for example, the ADC of the STM32 series should not exceed 3.3V). (2) Resolution: If the ADC's measurement range is 0-5V and the resolution is set to 12 bits, then the smallest voltage we can measure is 5V divided by 2 to the power of 12, which is 5/4096=0.00122V. Clearly, the higher the resolution, the more accurate the collected signal, making resolution an important indicator of ADC performance. (3) Sampling Time: When the ADC samples an external voltage signal at a certain moment, the external signal should remain unchanged. However, in reality, the external signal is constantly changing. Therefore, the ADC has a hold circuit that maintains the external signal at a certain moment, allowing the ADC to stabilize its collection. The time for which this signal is held is called the sampling time. (4) Sampling Rate: This refers to how many times the ADC samples within one second. Obviously, a higher sampling rate is better; when the sampling rate is insufficient, some information may be lost. Therefore, the ADC sampling rate is another important indicator of ADC performance (for detailed reference, see books on signal processing).1.2 ADC of STM32
STM32 has 1 to 3 ADCs (the STM32F101/102 series has only 1 ADC, while the STM32F103 series has 3 ADCs and 1 DAC). These ADCs can be used independently or in dual mode (to increase the sampling rate). The ADC of STM32 is a 12-bit successive approximation analog-to-digital converter. It has 18 channels, capable of measuring 16 external and 2 internal signal sources. The A/D conversion of each channel can be executed in single, continuous, scan, or discontinuous modes. The ADC results can be stored in a 16-bit data register in either left-aligned or right-aligned format.
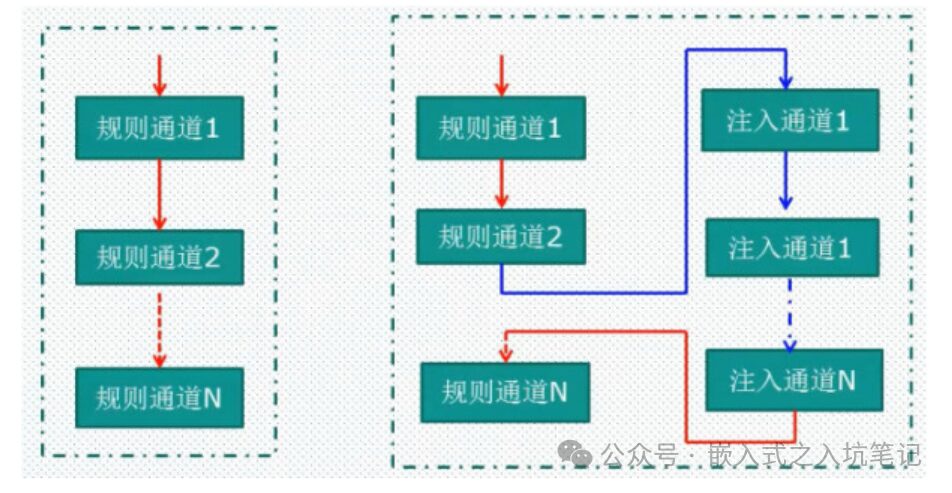
Note: The ADC is a 12-bit successive approximation type ADC, with output value range from 0 to 2^12 - 1 (0 to 4095), and the full scale is 3.3V. The resolution corresponds to the input voltage value of the least significant bit (LSB). Resolution = 3300/4095 ≈ 0.806mV.The STM32F10X series divides the ADC conversion into two channel groups: regular channel group and injected channel group. The regular channel is equivalent to the normal running program, while the injected channel can interrupt the regular channel selection. When the program is running normally, interrupts can interrupt the program execution. Similarly, the conversion of the injected channel can interrupt the conversion of the regular channel, and the regular channel can continue its conversion only after the injected channel conversion is completed.
2. VOFA+
2.1 Introduction to VOFA+
VOFA+ is an intuitive, flexible, and powerful plug-in driven upper computer that can be seen in fields dealing with electrical systems, such as automation, embedded systems, the Internet of Things, and robotics. The name VOFA+ comes from the basic electrical units: Volt, Ohm, Farad, and Ampere, named after their inventors—four giants in the field of electronic physics. Their initials together form the name VOFA+.

Overview of VOFA+ features: Platform support: Windows, Linux, MacOS; Interface support: Serial port (high baud rate, stable support), network port (TCP client/server, UDP); Protocol support: Protocols are plug-ins, open-source, and anyone can write them. Currently supports CSV-style string protocols and hexadecimal floating-point array byte stream protocols; Control support: Controls are plug-ins, open-source, and anyone can write them. Currently supports waveform graphs, buttons, status lights, images, sliders, 3D cube controls (model replacement available), etc.; Data dimension flexibility: 2D and 3D, both must be present; Self-developed waveform control: supports drawing millions of sampling points per channel, strong performance; Self-developed waveform control: seamlessly integrates real-time histogram statistics and Fourier transforms with adjustable point counts, allowing data analysis using VOFA+.2.2 How to Use VOFA+
VOFA+’s data protocol engine has three types: FireWater, JustFloat, and RawData. Each data protocol engine has its special effects, and readers can choose based on their actual needs. Here, the author mainly demonstrates the usage effects and methods of VOFA+ under the FireWater protocol.
The FireWater protocol is a CSV-style string stream, which is intuitive and simple, with programming as easy as printf. However, since string parsing consumes more computational resources (both on the upper and lower computers), it is recommended to use it only when the number of channels is not high and the sending frequency is low.
Hover overFireWater protocolto get helpful usage format guidance. As shown in the above image, we use the function printf(“simples:%f, %f\n”, sin(t1), sin(t2)) for printing tests.
#include "math.h"#include "stdio.h"....int main(void){ /* USER CODE BEGIN 1 */ float t1 = 0; float t2 = 0; /* USER CODE END 1 */....while (1) { /* USER CODE END WHILE */ /* USER CODE BEGIN 3 */ t1 += 0.1; t2 += 0.5; printf("simples:%f, %f\n", sin(t1), sin(t2)); HAL_Delay(100); } /* USER CODE END 3 */}1. Set serial communication, port number, baud rate, and other parameter settings;
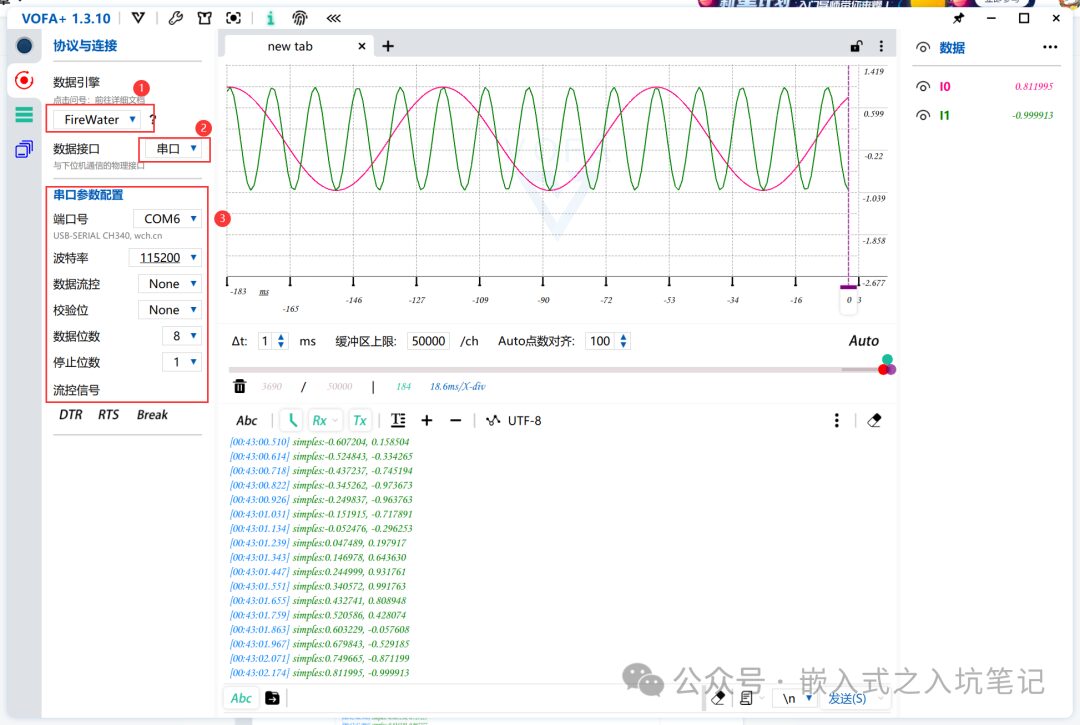
2. Select the waveform graph in the controls, drag it into the tab, right-click to select the Y-axis to include both inputs I0 and I1, and then establish the serial connection;
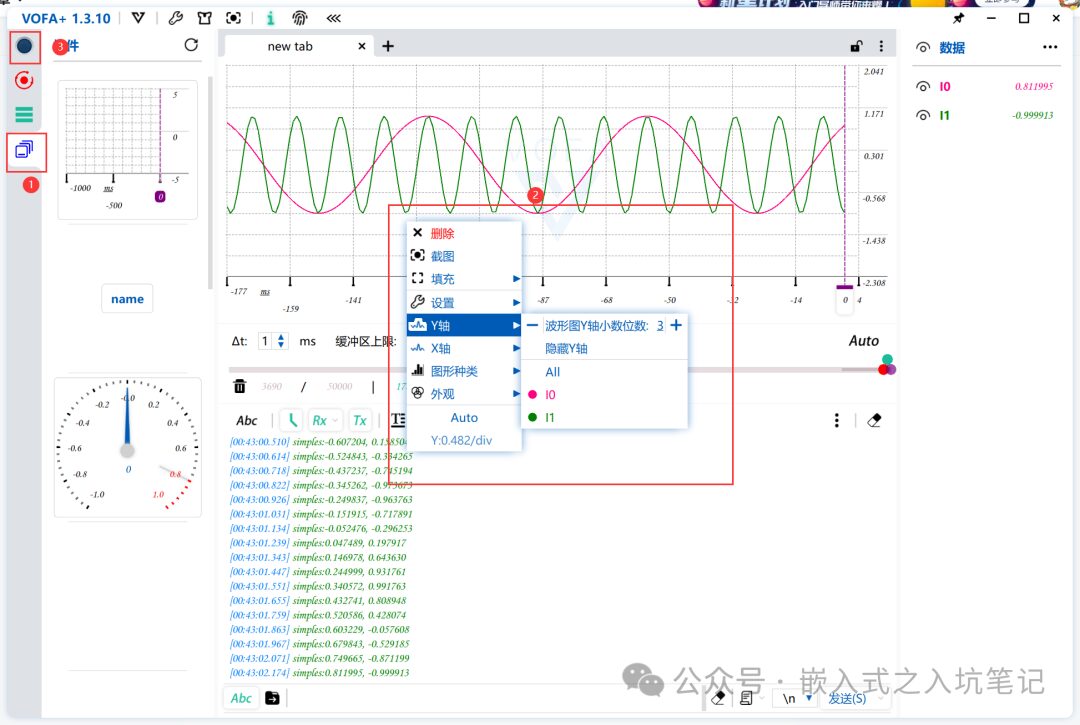
3. Run the upper computer and use the waveform graph control to read parameters from the lower computer;
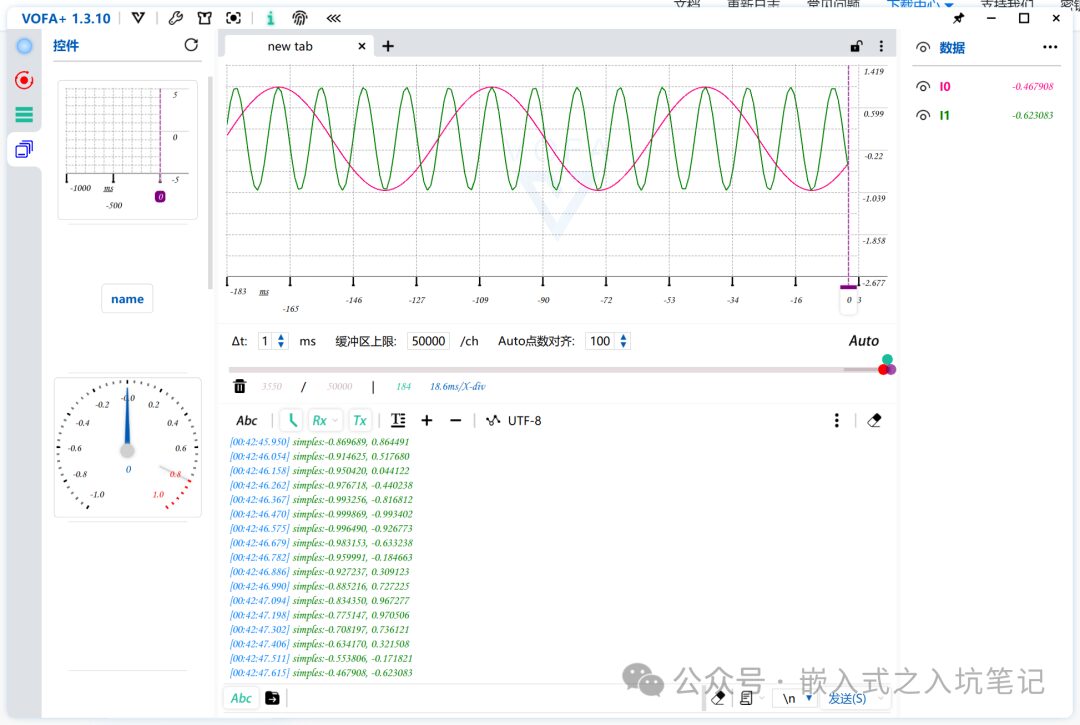
3. Filtering Algorithms and Effects
Due to the inherent defects of the MCU's ADC peripherals, its accuracy and stability are usually poor, and filtering compensation is often necessary in many scenarios. The role of filtering is to reduce the impact of noise and interference on data measurement.3.1 Sampling Without Filtering Algorithm
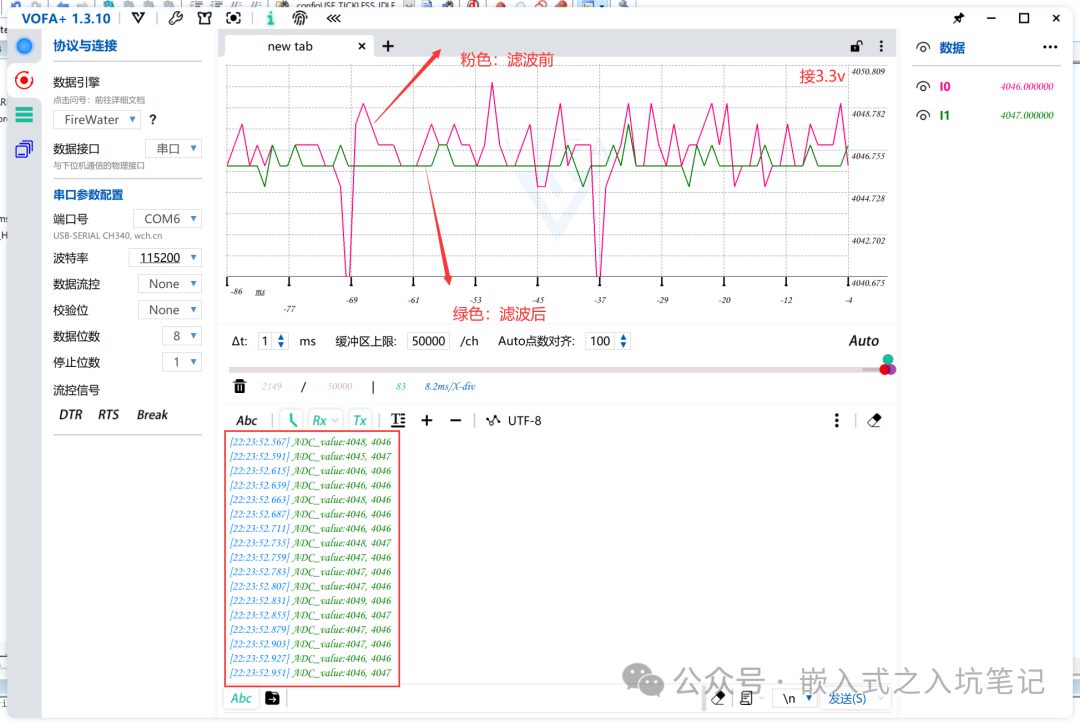
Directly sampling a voltage of 3.3V:
Data read by VOFA+:
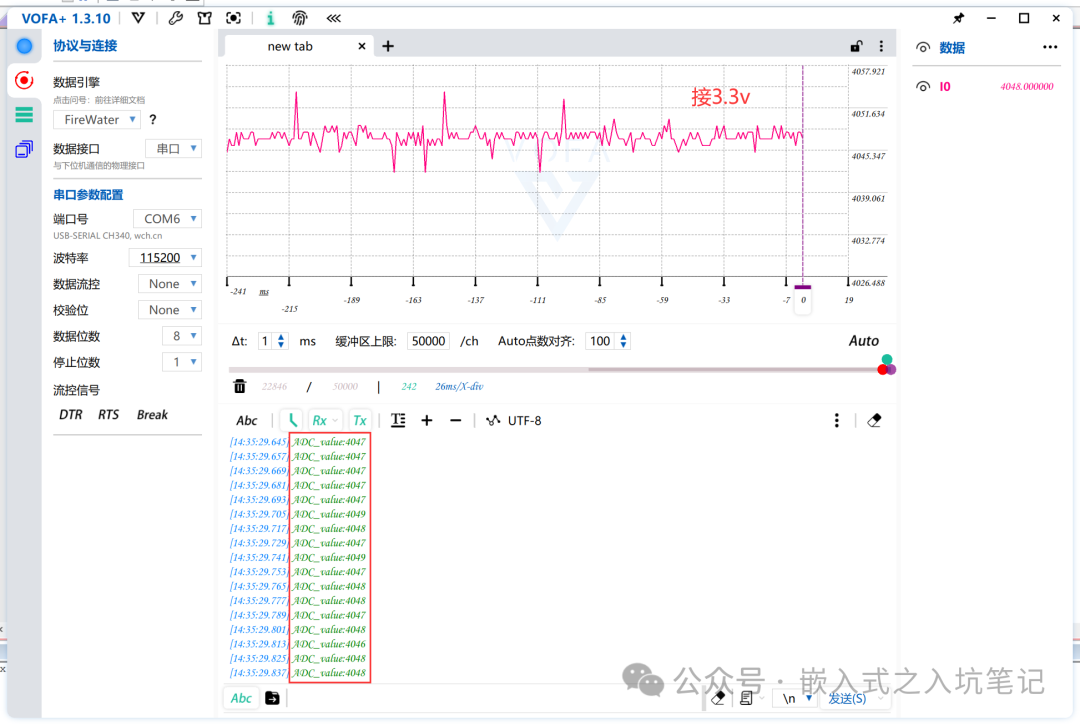
The above image clearly shows that the ADC sampling without filtering fluctuates significantly, but the author subjectively feels that the ADC of the F1 series seems to be more stable than that of the F4 series. (The reason it is not 4096 may be because the power supply has not reached 3.3V).
4. Filtering Algorithms
4.1 First-Order Complementary Filter
Method: Take a=0~1, this filtering result = (1-a) current sample value + a previous filtering result. Advantages: Good suppression of periodic interference; suitable for scenarios with high fluctuation frequency. Disadvantages: Phase lag, low sensitivity; the degree of lag depends on the value of a; cannot eliminate interference signals with filtering frequencies higher than half the sampling frequency.The code is as follows:
// First-order complementary filterint firstOrderFilter(int newValue, int oldValue, float a){ return a * newValue + (1-a) * oldValue;}ADC_value=HAL_ADC_GetValue(&hadc1); // Get ADC1 value// Main functionwhile(1){ HAL_ADC_Start(&hadc1); // Start ADC1, place in while loop Filtering_Value = firstOrderFilter(HAL_ADC_GetValue(&hadc1),ADC_value,0.3); // Filtering algorithm HAL_Delay(10); // Delay function to prevent sampling failure printf("ADC_value:%d\n", ADC_value);}Effect Diagram of VOFA+ Software:
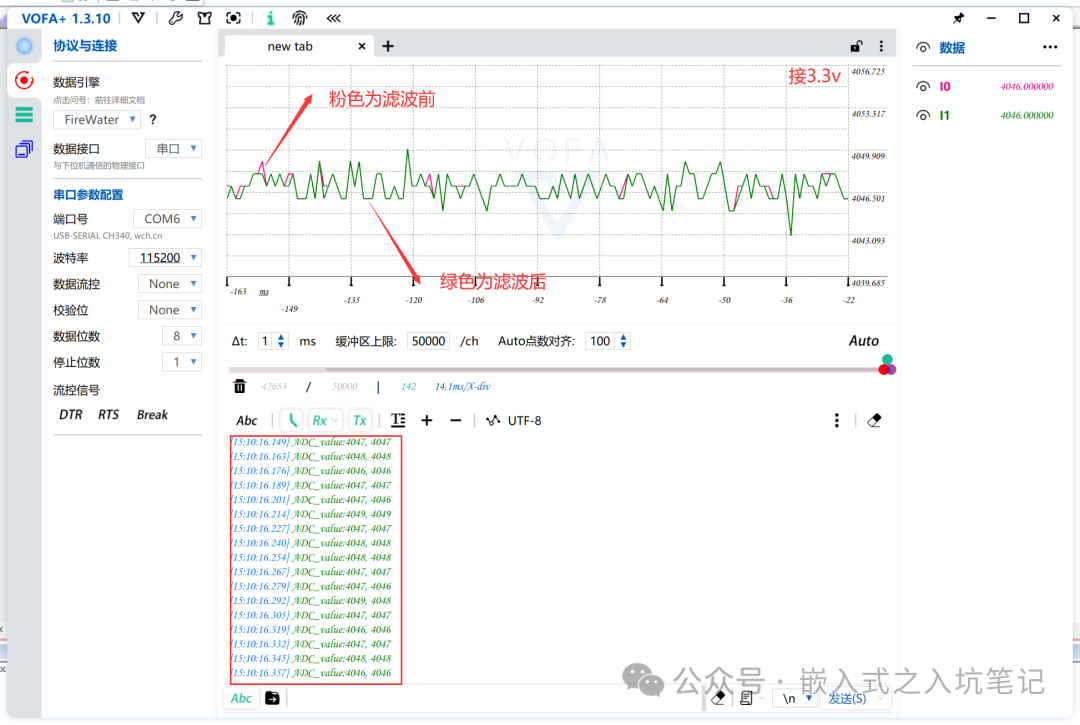
Conclusion:
The limitations of the first-order complementary filter are significant, and its effectiveness is quite average.4.2 Median Filtering
Method: Continuously sample N times (N must be odd), sort the N sampled values by size, and take the middle value as the effective value. Advantages: Effectively overcomes fluctuations caused by random factors; has good filtering effects for slowly changing measured parameters such as temperature and liquid level. Disadvantages: Not suitable for rapidly changing parameters such as flow and speed.The code is as follows:
// Median filtering algorithmint middleValueFilter(int N){ int value_buf[N]; int i,j,k,temp; for( i = 0; i < N; ++i) { value_buf[i] = HAL_ADC_GetValue(&hadc1); } for(j = 0 ; j < N-1; ++j) { for(k = 0; k < N-j-1; ++k) { // Sort in ascending order using bubble sort if(value_buf[k] > value_buf[k+1]) { temp = value_buf[k]; value_buf[k] = value_buf[k+1]; value_buf[k+1] = temp; } } } return value_buf[(N-1)/2];}Effect Diagram of VOFA+ Software:
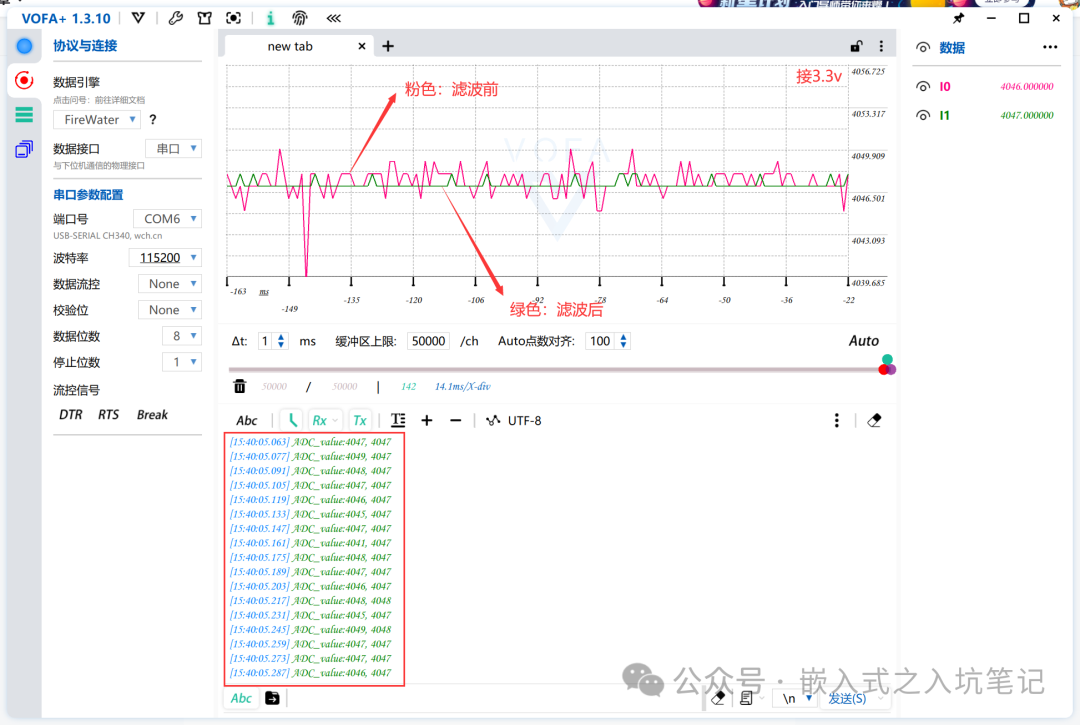
Conclusion:
Median filtering is very effective in eliminating outliers and stabilizing ADC sampling.4.3 Arithmetic Mean Filtering
Method: Continuously take N sampling values for arithmetic averaging; when N is large: higher signal smoothness, but lower sensitivity; when N is small: lower signal smoothness, but higher sensitivity. Selection of N: generally for flow, N=12; for pressure, N=4. Advantages: Suitable for filtering signals with random interference, characterized by an average value, fluctuating around a certain value range. Disadvantages: Not suitable for real-time control requiring fast data calculations.The code is as follows:
// Arithmetic mean filteringint averageFilter(int N){ int sum = 0; short i; for(i = 0; i < N; ++i) { sum += HAL_ADC_GetValue(&hadc1); } return sum/N;}Effect Diagram of VOFA+ Software:
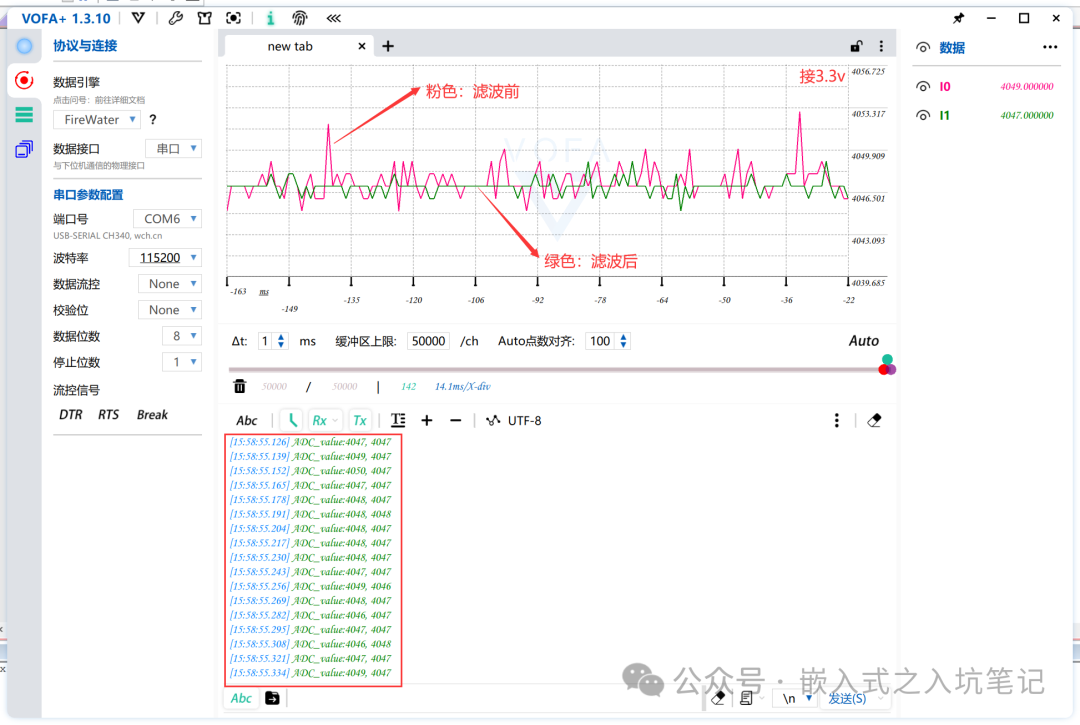
Conclusion:
Arithmetic mean filtering shows a certain level of stability while also exhibiting fluctuations (reasonable selection of N can yield good results).4.4 Sliding Average Filtering
Method: Treat the continuous N sampling values as a queue with a fixed length of N. Each time a new data point is sampled, it is added to the end of the queue while the oldest data point is removed (FIFO principle). The arithmetic average of the N data points in the queue yields the new filtering result. Selection of N: for flow, N=12; for pressure, N=4; for liquid level, N=4~12; for temperature, N=1~4. Advantages: Good suppression of periodic interference, high smoothness; suitable for systems with high-frequency oscillations. Disadvantages: Low sensitivity; poor suppression of sporadic pulse interference, not suitable for scenarios with severe pulse interference; relatively high RAM consumption (improvement method: do not remove the oldest value, but rather the last obtained average value).Code:
// Smooth average filtering#define N 10int value_buf[N];int sum=0;int curNum=0;int moveAverageFilter(){ if(curNum < N) { value_buf[curNum] = HAL_ADC_GetValue(&hadc1); sum += value_buf[curNum]; curNum++; return sum/curNum; } else { sum -= sum/N; sum += HAL_ADC_GetValue(&hadc1); return sum/N; }}Effect Diagram of VOFA+ Software:
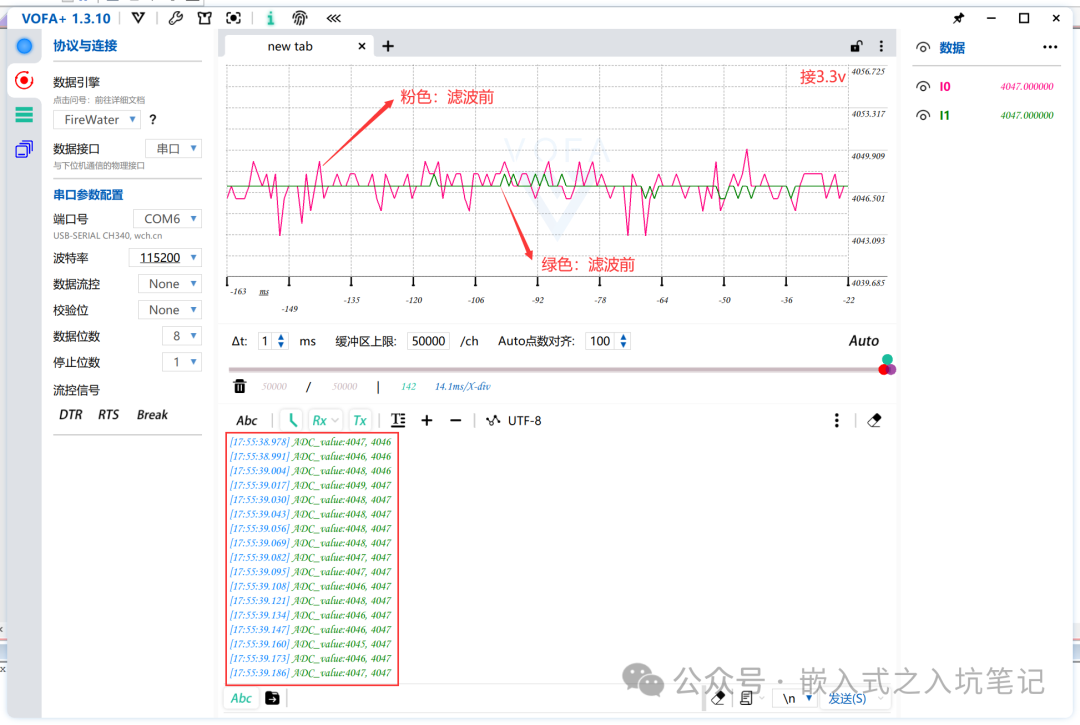
Conclusion:
Sliding average filtering stands out for its smooth characteristics compared to regular arithmetic mean filtering. The waveform graph from VOFA+ shows that smooth filtering can effectively mitigate ADC sampling noise and stabilize data collection (based on practical feedback from the author's peers, the effect of smooth filtering is notably good, especially in control applications).4.5 Clipping Average Filtering
Method: Equivalent to "clipping filtering method" + "recursive average filtering method". Each time a new data point is sampled, it is first subjected to clipping processing before being sent to the queue for recursive average filtering. Advantages: Can eliminate sampling value deviations caused by sporadic pulse interference. Disadvantages: Relatively high RAM consumption.The code is as follows:
// Clipping average filtering#define A 50 // Clipping threshold#define M 12int data[M];int First_flag=0;int LAverageFilter(){ int i; int temp,sum,flag=0; data[0] = HAL_ADC_GetValue(&hadc1); for(i=1;i<M;i++) { temp=HAL_ADC_GetValue(&hadc1); if((temp-data[i-1])>A || ((data[i-1]-temp)>A)) { i--; flag++; } else { data[i]=temp; } } for(i=0;i<M;i++) { sum+=data[i]; } return sum/M;}Effect Diagram of VOFA+ Software:
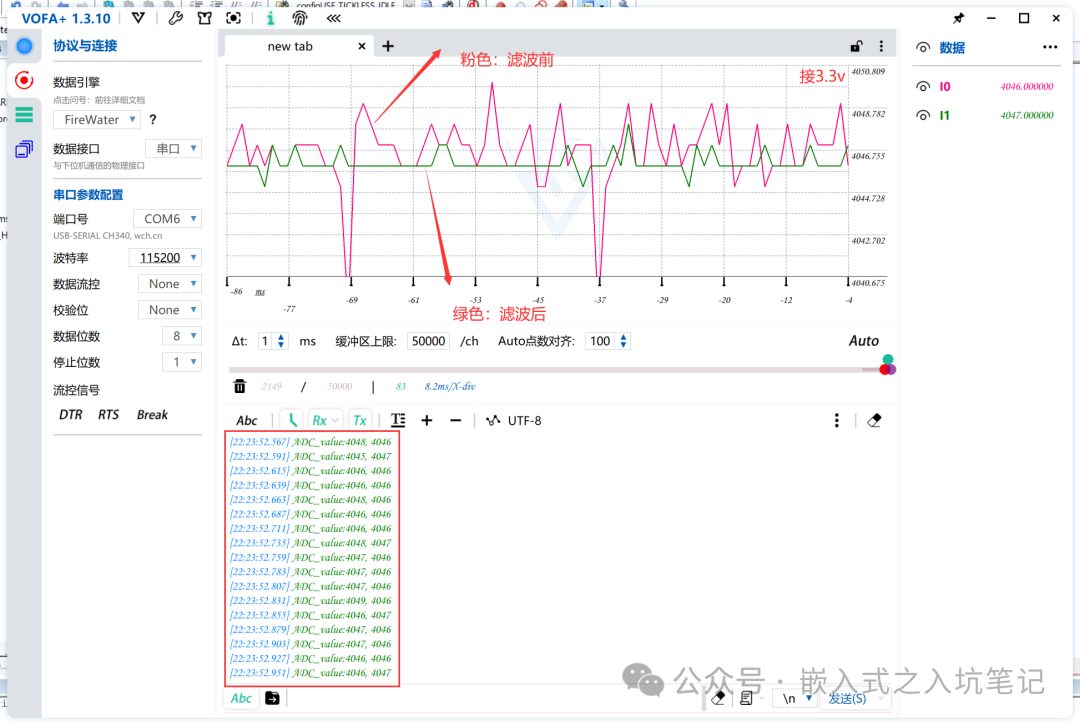
Conclusion:
Clipping average filtering is similar to a patchwork approach, but its effects are very significant; it effectively addresses the impact of sudden noise on ADC sampling in practical scenarios, although it consumes memory.4.6 Kalman Filtering
Core Idea: Based on the current "measured value" of the instrument and the "predicted value" and "error" from the previous moment, calculate the current optimal value and predict the next moment's value. A prominent feature is the incorporation of errors into the calculations, which are classified into prediction errors and measurement errors, collectively referred to as noise. Another significant characteristic is that errors exist independently and are not influenced by measurement data. Advantages: Ingeniously integrates observed data with estimated data, manages errors in a closed loop, and confines errors within a certain range. Applicable across a wide range, with excellent timeliness and effectiveness. Disadvantages: Requires parameter tuning, as the size of the parameters significantly impacts filtering effectiveness.Code:
// Kalman filteringint KalmanFilter(int inData){ static float prevData = 0; // Previous value static float p = 10, q = 0.001, r = 0.001, kGain = 0; // q controls error r controls response speed p = p + q; kGain = p / ( p + r ); // Calculate Kalman gain inData = prevData + ( kGain * ( inData - prevData ) ); // Calculate the estimated value for this filtering p = ( 1 - kGain ) * p; // Update measurement variance prevData = inData; return inData; // Return filtered value}Effect Diagram of VOFA+ Software:
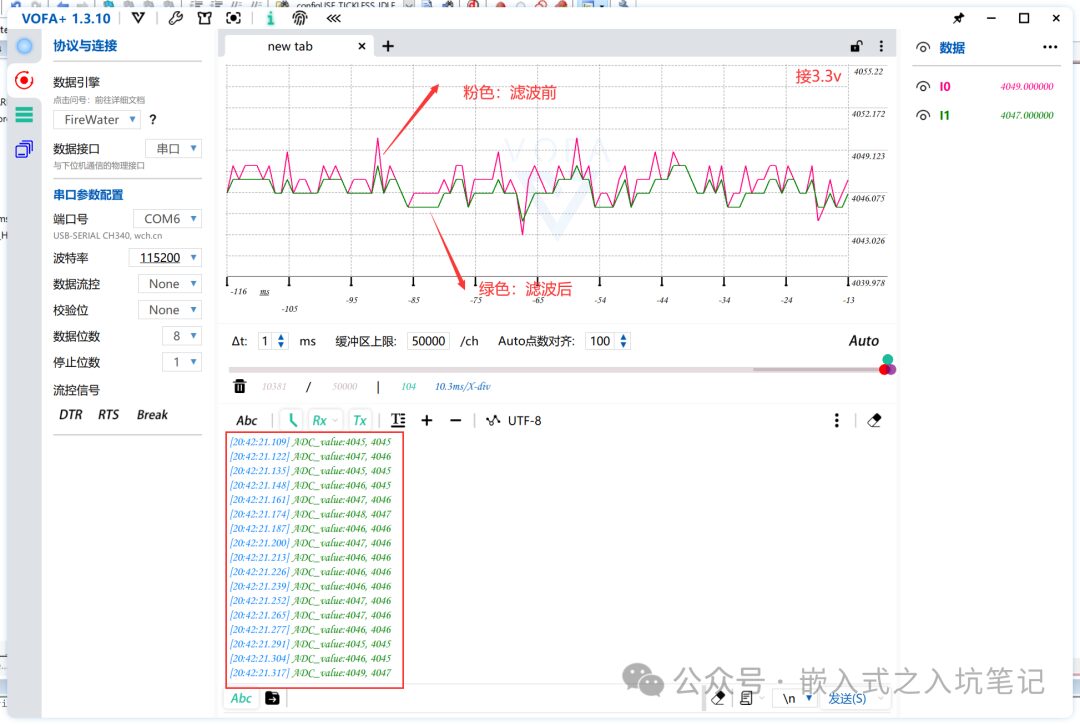
Conclusion:
The waveform graph displayed by VOFA+ shows that Kalman filtering has certain noise reduction and stabilization characteristics, although its effectiveness is not particularly outstanding. Kalman filtering is highly versatile, especially in control and multi-sensor fusion applications; as long as the parameters are well-tuned, the results can be surprisingly excellent.5. Experimental Summary
As an essential peripheral that must be mastered in embedded development, ADC often requires the configuration of filters in projects. If the RC hardware filtering effect is average, software can be used to compensate. At the same time, there are various filtering algorithms, each with different principles. I hope that readers do not blindly pursue various sophisticated filtering algorithms in actual engineering projects; suitable filtering for the project is good filtering.
Original Source:
Link: https://blog.csdn.net/black_sneak/article/details/129629485