📌 Problem Description

Write a program to output the first n terms of the Fibonacci sequence (starting from 1, in the form of 1, 1, 2, 3, 5…).

Requirements:1. Support input of any positive integer n2. Optimize time complexity to O(n)Example:

Input: n=5 → Output: 1 1 2 3 5  Input: n=1 → Output: 1  

Difficulty: ⭐ (suitable for learners mastering loops and recursion)

💡 Basic Implementation (Iterative Method)

#include <stdio.h>
void print_fibonacci(int n) {    if (n < 1) return;    int a = 1, b = 1;    printf("The first %d terms of the Fibonacci sequence:", n);    for (int i = 0; i < n; i++) {        printf("%d ", a);        int next = a + b;        a = b;        b = next;    }}
int main() {    int n;    printf("Input n:");    scanf("%d", &n);    print_fibonacci(n);    return 0;}

Output Example:

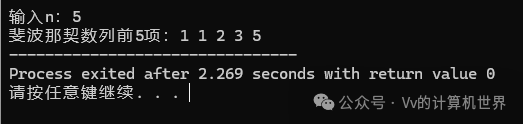
🔥 Recursive Implementation (Understanding the Concept, Not Recommended for Practical Use)

#include <stdio.h>
int fib(int n) {    if (n == 1 || n == 2) return 1;    return fib(n - 1) + fib(n - 2);}
int main() {    int n;    printf("Please enter the number of Fibonacci sequence terms to calculate: ");    scanf("%d", &n);
    if (n <= 0) {        printf("The number of terms must be a positive integer.\n");        return 1;    }
    printf("The first %d terms of the Fibonacci sequence are: ", n);    for (int i = 1; i <= n; i++) {        printf("%d ", fib(i));    }    printf("\n");
    return 0;}    // Note: Recursive method has a time complexity of O(2ⁿ), suitable only for teaching demonstration

🔥 Optimized Implementation (Advanced: Dynamic Programming)

#include <stdio.h>
void print_fib_opt(int n) {    if (n < 1) return;    int dp[n];    dp[0] = dp[1] = 1;    for (int i = 2; i < n; i++) {        dp[i] = dp[i - 1] + dp[i - 2];    }    for (int i = 0; i < n; i++) {        printf("%d ", dp[i]);    }    printf("\n");}
int main() {    int n;    printf("Please enter the number of Fibonacci sequence terms to calculate: ");    if (scanf("%d", &n) != 1) {        printf("Invalid input, please enter an integer.\n");        return 1;    }    if (n <= 0) {        printf("The number of terms must be a positive integer.\n");        return 1;    }    printf("The first %d terms of the Fibonacci sequence are: ", n);    print_fib_opt(n);    return 0;}    

Advantages：

• Time complexity O(n), space complexity O(n)

• Can quickly query the value of any term

🤔 Common Problem Analysis

Problem	Error Code	Correct Implementation
Boundary case n=0 not handled	Direct loop causes crash	Add<span>if (n < 1) return</span>
Incorrect number of output terms	<span>i <= n</span> → Outputs one extra term	<span>i < n</span>
Value overflow	Did not handle large n causing int overflow	Change to<span>long long</span> type

🎯 Extension Challenge

Try to implement the following features (choose any one)：

1. Output the nth term (without using an array, space complexity O(1))

2. Support large number output (e.g., n=100, using string handling)

3. Graphically print the sequence (spiral arrangement, triangle, etc.)

🚀 Next Issue Preview No. 18 Pascal’s Triangle: Can You Print a Symmetrical Triangle Using a Two-Dimensional Array?

📢 Interaction Time

1. What other fascinating properties of the Fibonacci sequence do you know? Feel free to leave a comment!

2. Vote:

🚀 If you find it useful, feel free to share it with friends learning C language!

Article Author:Vv Computer Graduate Examination World (focusing on computer graduate examination guidance for8 years)

Original Statement: Please contact for authorization to reprint, infringement will be pursued.