For some inference tasks of large models, the bottleneck is not computational power (FLOPS).
Recently, many people in the open-source community have been exploring optimization methods for large models. A project called llama.cpp has rewritten the inference code of LLaMa in pure C++, achieving excellent results and gaining widespread attention.

Through some optimizations and weight quantization, it allows us to run the LLaMa model locally on various hardware we previously couldn’t imagine. Among them:
-
On a Google Pixel 5, it can run a 7B parameter model at a speed of 1 token/s.
-
On an M2 chip MacBook Pro, the speed using a 7B parameter model is about 16 token/s.
-
We can even run a 7B model on a Raspberry Pi with 4GB RAM, although the speed is only 0.1 token/s.
GitHub link: https://github.com/ggerganov/llama.cpp
We know that apart from generalization capabilities, the key to deploying large models lies in optimizing inference performance. However, the current level of optimization has exceeded our expectations. As of now, llama.cpp has garnered 38,000 stars on GitHub, almost as many as the LLaMa model itself. By June, the author of llama.cpp, Georgi Gerganov, simply started a business, announcing the establishment of a new company, ggml.ai, aimed at reducing the operating costs of large models using a pure C language framework.
Many people may wonder at this point: how is this possible? Don’t large language models require GPUs like the NVIDIA H100 to run? To address this confusion, someone recently delved into the mathematics surrounding large model inference and attempted to provide answers.
Let’s start with “Why do AI training tasks require GPUs?” GPUs have two main advantages for deep learning:
-
They have a large memory bandwidth (e.g., A100: 1935 GB/s, RTX 4090: 1008 GB/s).
-
They have significant computing power (A100: 312 TFLOPS for FP16, RTX 4090: 82.6 TFLOPS for FP16).
The importance of memory bandwidth lies in the time required for data to move from HBM memory (i.e., RAM) to on-chip memory. When using GPUs for mathematical calculations, we need to transfer the relevant matrices to on-chip memory, which is relatively small (40MB on A100, while RAM is 40-80GB). Memory bandwidth is approximately two orders of magnitude smaller than computational performance — this will be important later, as memory bandwidth is often the bottleneck in inference.
From a computer architecture perspective, we need to categorize memory with different speeds and capacities into levels to pursue a balance between efficiency and cost. Frequently accessed data is placed in the fastest but smallest registers and L1 cache, while the least accessed data is stored in the slowest and largest memory modules.
What does this mean for LLaMa inference tasks? Let’s start with some mathematical calculations for inference. We can use Kipply’s article (https://kipp.ly/transformer-param-count/) to make some rough calculations of LLM’s inference performance.
First, regarding model size:
-
The shapes of the Q, K, and V weight matrices are all [d_model, d_head], with n_heads for each layer; the attention output matrix has the same shape, totaling 4 * [d_model, n_heads * d_head]. By convention, GPT-style networks have d_head * n_heads = d_model.
-
MLP has two weight matrices, shaped [d_model, 4 * d_model] and [4 * d_model, d_model].
-
The embedding matrix size is [d_vocab, d_model].
This gives us a convenient equation for the number of parameters in a GPT-like model:
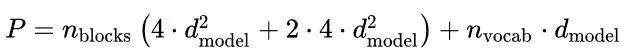
Here, we will focus on the scenario of running ChatGPT-like services locally, which is what llama.cpp does. Let’s assume a batch size of 1. For efficient inference, the KV cache must be stored in memory; the KV cache needs to store the KV values for each layer, which amounts to storing: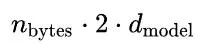
Here, n_bytes represents the number of bytes per parameter; for float32 it is 4, for float16 it is 2, and so on. The middle 2 is because we need to store one set of weights for K values and one set for V values.
Given an n-layer model, the total memory for the KV cache is: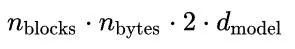
In addition to storing the KV cache in memory, we also need to store the weights themselves in memory; this requires n_bytes * P bytes.
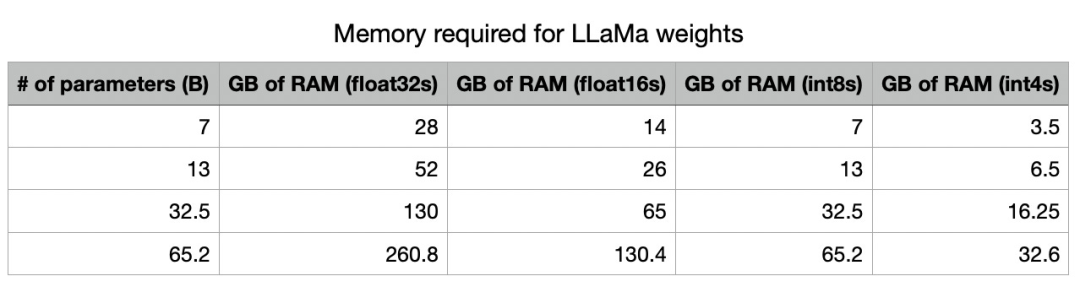
This is one of the main advantages of quantization. By using lower precision, we can fundamentally reduce the amount of memory required to store the model. Note that at int4 precision, all these models fit into the memory of NVIDIA’s A100 (which is also a common GPU in data centers), and all models except the largest ones fit into high-end consumer GPUs (such as RTX 3090/4090 with 24GB RAM).
Now, when it comes to actual inference running, each token requires about 2P FLOPS, as we are performing a series of matrix multiplications using a total of P parameters, with matrix sizes being (m, n) vector (n,), costing 200 mn.
After completing all the mathematical calculations, let’s calculate the requirements for running inference using LLaMa. The main requirements for sampling are:
-
In addition to all parameters, keep the KV cache in memory.
-
Read all weights from HBM into on-chip storage. Since we are performing autoregressive sampling, we must repeat this for each token sampled.
-
Perform actual matrix multiplications to compute the output of our network.
Latency is the maximum of computational latency or memory latency, as loading parameters into on-chip memory occurs asynchronously in all modern tensor programming libraries. Therefore, we write:
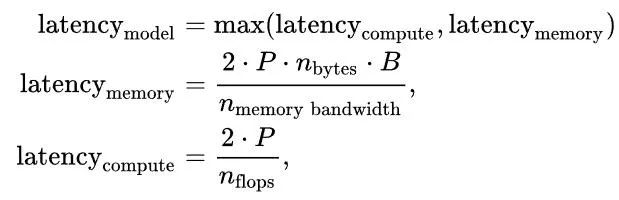
Where B is the batch size. Given that memory bandwidth is approximately 1.935e12 and the required FLOPS is about 3.12e14, as long as the batch size is less than 161, the model will be memory constrained.
When the batch size is 1, that is, generating a single prediction stream on the computer, this is the same equation, just like on most hardware (like NVIDIA’s GPUs); when you lower precision, linear acceleration occurs: using fp16 instead of fp32 doubles FLOPS, switching to int8 doubles FLOPS again, and using int4 doubles FLOPS once more.
Since llama.cpp uses a relatively aggressive int4 format in current deep learning inference, the RAM requirement for the KV cache reduces to 1.33GB, and the VRAM for model parameters reduces to 16.25GB. This looks promising.
Since memory bandwidth is almost always much smaller than FLOPS, memory bandwidth is the bottleneck.
Note that the number of FLOPS/token required is the same as the memory bandwidth required because we must 1) load all parameters into on-chip memory, and then 2) use those parameters to compute the results. All of these occur simultaneously, as all modern tensor programming frameworks can asynchronously handle the “load into memory” part, so the total time required is max(compute time, memory time).
Running LLaMa on NVIDIA A100
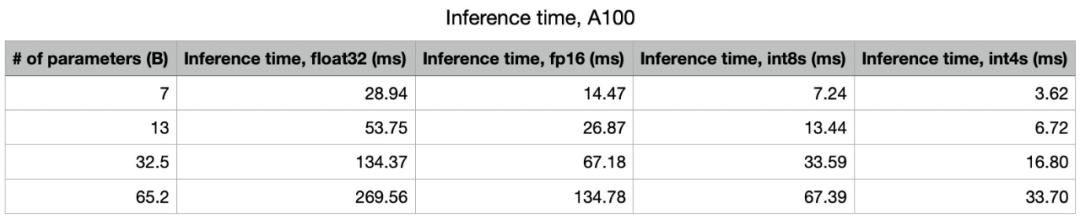
On the A100 (80GB PCIe), memory bandwidth is 1935GB/s. The int4 compute capacity is 1248 TOPS. Therefore, the model is severely limited by memory. We expect the speed of the 65B model to be around 30 token/s, while the speed of the 7B model is around 277 token/s.
Running LLaMa on MacBook
Next is the main content, the M1 chip commonly found on Apple MacBooks has a bandwidth of 68.25 GB/s, and the M1 GPU can perform up to 5.5 TFLOPS of fp16 computation. Therefore, we expect the sampling limit for a 65B model using int4 to be around 1 token/s, while the sampling limit for a 7B model is around 10 token/s.
Since the M2 Pro chip has a bandwidth of 200 GB/s, and the M2 Max has a bandwidth of 400 GB/s, we should expect huge performance gains here, with the M2 Max being able to achieve about 6 token/s when using the 65B model. This is already quite impressive for a laptop.
Running LLaMa on Raspberry Pi 4
The Raspberry Pi 4 has a computing capacity of 13.5 GFLOPS and about 4GB/s of memory bandwidth. Given this, if the 7B model is memory constrained, we expect to see an inference speed of about 2 token/s. However, what we currently observe is about 0.1 token/s, raising doubts that this is actually due to computational limitations. This attempt was made under conditions where hardware performance was unknown — we couldn’t find sufficient information on low-precision computing specifications for Raspberry Pi to determine this.
Summary
Memory bandwidth is almost the major limiting factor associated with transformer sampling. Any method to reduce these models’ memory requirements will make them easier to serve — such as quantization! This is another important reason for distillation (or simply training smaller models for a long time).
OpenAI scientist Andrej Karpathy further explained this observation.

He stated: In addition to parallel inference and training, prompt encoding can even be parallelized at batch_size = 1, as prompt tokens can be encoded by the LLM in parallel rather than decoded serially one by one. As the prompts become longer, the inference performance of the MacBook will lag further behind that of the A100.
On the other hand, Apple’s M2 chip appears to demonstrate strong capabilities in large model inference tasks. “Therefore, the M2 Ultra is currently the smallest, most beautiful, out-of-the-box, simplest, and most powerful personal LLM node.”
Chen Tianqi also agrees with this view.

Of course, none of this comes for free. Essentially, using low precision comes with some loss of accuracy and may result in some odd responses, causing the large model’s responses to go off track or produce hallucinations. However, as the number of model parameters increases, the quality loss becomes lower. Therefore, for very large models, the differences may be negligible. Moreover, this is just the inference cost. Training is a completely different matter.
Through the trade-offs of various performance parameters, we may soon truly have more “intelligent” devices.
Reference content:
https://finbarrtimbers.substack.com/p/how-is-llamacpp-possible
https://news.ycombinator.com/item?id=37140013
https://twitter.com/karpathy/status/1691571869051445433
72 PNGs, Illustrated Machine Learning
Jupyter Major Upgrade! AI-powered, Chat and Code Writing
10 Most Common Hyperparameter Tuning Guides in XGBoost
PyTorch Code Repository! 60+ Algorithm Implementations of Classic Deep Learning Papers & Line-by-line Explanations
Possibly the Most Comprehensive Cheat Sheet on the Internet: Python, Numpy, Pandas, Matplotlib, Machine Learning, ChatGPT, etc.
